МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»

(наименование института полностью)

(Наименование учебного структурного подразделения)

09.03.03 Прикладная информатика

(код и наименование направления подготовки / специальности)

Бизнес-информатика

(направленность (профиль) / специализация)

Практическое задание №1
по учебному курсу «Линейная алгебра и аналитическая геометрия»

^{(наименование учебного курса)}
Вариант 5

Обучающегося
	(И.О. Фамилия)
Группа	ПИбд-1902а
Преподаватель	Демченкова Н.А.
	(И.О. Фамилия)

Тольятти 2023

Задание

Дана система уравнений. Доказать ее совместность. Найти решение системы следующими способами: используя метод Гаусса,

---

средства матричного исчисления, формулы Крамера.



Решение. 1. Докажем совместность системы: составим основную и расширенные матрицы:



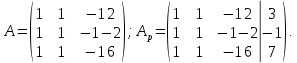
Найдем ранги матриц:



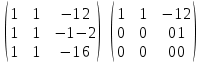
Ранг матрицы A равен 2.



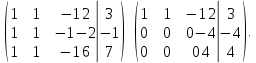
Ранг расширенной матрицы равен 3, следовательно, система не совместна.

2. Решим систему методом Гаусса:



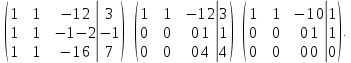
Находим решение, начиная с нижнего уравнения, поднимаясь снизу вверх:

x1 = 1 - x2 + x3

x4 = 1

x2, x3 - свободные

Остальное решить не получилось..

---

Смотрите также файлы

• Статья 197 гк рф предусматривает для отдельных видов требований возможность установления законодательством специальных сроков исковой давности, сокращенных или более длительных по сравнению с общим сроком.docx

• Экзаменационные вопросы для лечебного и педиатрического факультетов 20172018 учебный год.doc

• Программа среднего профессионального образования 40. 02. 01. Право и организация социального обеспечения.pdf

• Технология печати книжного издания в твердом переплете на примере, издания "Ежедневник".docx

• Осмотр места происшествия и трупа.pdf