Файл: Контрольная работа по дисциплине Теория автоматического управления Вариант 0 фио Федоров Антон Алексеевич.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.10.2023
Просмотров: 42
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. Бонч-Бруевича
(СПБГУТ)

«ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ (ИНО)»
Контрольная работа по дисциплине
«Теория автоматического управления»
Вариант 0
ФИО: Федоров Антон Алексеевич
Факультет: ИНО
Курс: 3
Группа: ПБ-11з
Студенческий билет: 2005450
Теория автоматического управления
Контрольная работа
Вариант 0
Вопрос: Система автоматической стабилизации.
Задание: Для колебательного звена второго порядка записать дифференциальное уравнение и уравнение передаточной функции.
Записать уравнение переходной функции и построить график переходной характеристики. Определить коэффициент относительного затухания
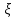 ,
,частоту колебаний
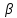 и их период
и их период 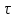 .
.Записать уравнение амплитудно-частотной и фазочастотной функций, рассчитать их и построить логарифмическое характеристики.
Параметры звена (Вариант 0)
| T1 | T2 | K |
| 0.4 | 0.03 | 15 |
Дифференциальное уравнение второго порядка описывается формулой:
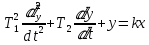 ,
,где x – входная величина, y – выходная величина
Откуда:
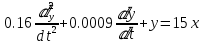
Уравнение передаточной функции колебательного звена:
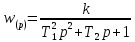 ,
,где p – символ дифференцирования.
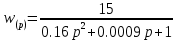
Коэффициент относительного затухания:
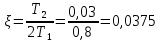
Частота колебаний:
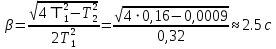
Период колебаний:
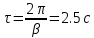
Переходная функция колебательного звена имеет вид:
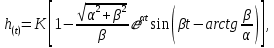
где
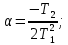
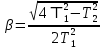
с использованием величины коэффициента относительного затухания:
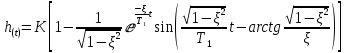
При всех известных:
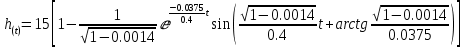
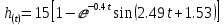
Значение времени t, соответствующее h(t)= K, обнуляется при:
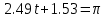
Откуда
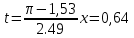 с.
с.Величина h(t)для моментов временистоящих друг от друга на четверть периода
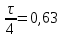 с.
с.При t = 0:
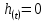
При t = 0,64 + 0,63 = 1,27 c.
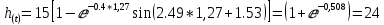
При t = 1,27 + 0,63 = 1,9 c.
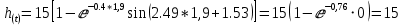
При t = 1,9 + 0,63 = 2,53 c.
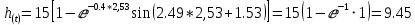
При t = 2,53 + 0,63 = 3,16 c.
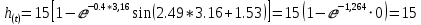
При t = 3.16 + 0,63 = 3,79 c.
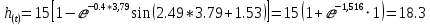
При t = 5,05 c.

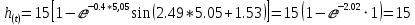
При t = 6,31 c.
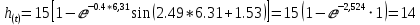
При t = 7,57 c.
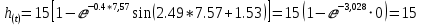
График переходной характеристики
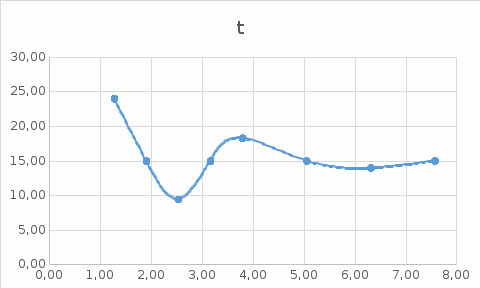
Амплитудная частотная характеристика описывается формулой:
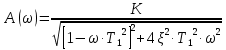
При:
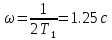 :
: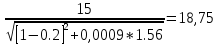
При:
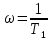 = 2.5с:
= 2.5с: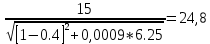
При:
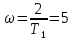 :
: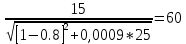
При:
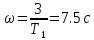 :
: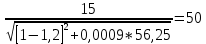
При:
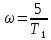 = 12.5:
= 12.5: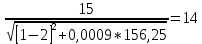
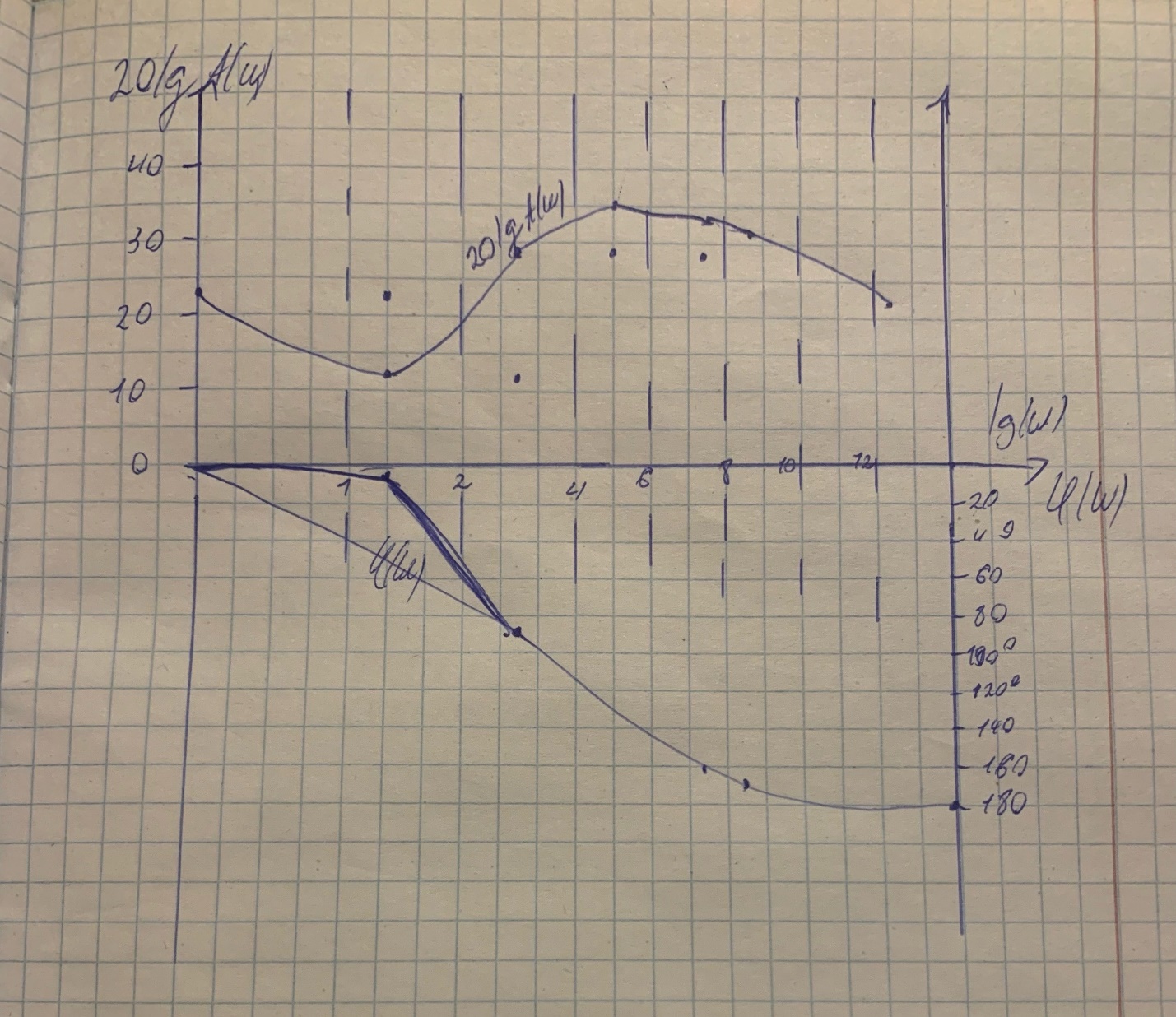
Логарифмическая частотная характеристика:
Lg
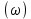 – абсцисса
– абсцисса20lgA(
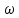 ) – ордината
) – ордината20lg15 = 23,52 дБ
20lg18,75= 13,4 дБ
20lg24,8 = 27,88 дБ
20lg60 = 35,56 дБ
20lg50 = 33,97 дБ
20lg14 = 22,92 дБ
Для уравнений
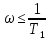 уравнение фазочастотной характеристики имеет вид:
уравнение фазочастотной характеристики имеет вид: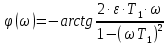
При:
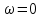 :
: 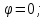
При:
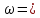 1.25с:
1.25с: 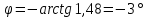
При:
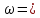 2.5с:
2.5с: 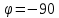
Для уравнений
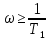 уравнение фазочастотной характеристики имеет вид:
уравнение фазочастотной характеристики имеет вид: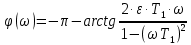
При:
 5:
5: 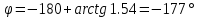
При:
 7.5с:
7.5с: 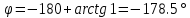
При:
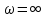 :
: 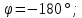
Ответ на вопрос:
Принцип регулирования по отклонению состоит в том, что измеряется регулируемая величина [δoc (t)], сравнивается с требуемым значением (задающим воздействием) [α(t)] и выявляющееся при этом отклонение [Δ(t)] преобразуется в регулирующее воздействие [μ(t)]. Последнее, влияя на объект регулирования, стремится уменьшить или устранить это отклонение. ИЭ, ЭС, УУ, ИМ образуют регулятор.
В отличие от САР с принципом по возмущению здесь регулирующее воздействие является функцией не возмущающего или задающего воздействия, а отклонения регулируемой величины, вызванного этим воздействием.Измерительный элемент, который измеряет регулируемую величину на выходе объекта и подает её на элемент сравнения (вход системы) образует главную обратную связь. Как видно из рисунка, в САР с принципом по отклонению регулируемая величина через главную обратную связь поступает на элемент сравнения (вход системы), т.е. САР с принципом по отклонению является замкнутой.
Замкнутые САР реагируют на любые возмущения, приводящие к изменению регулируемой величины, и в этом их достоинство.
Недостатком замкнутых САР является то, что при определенных условиях они могут оказаться неустойчивыми.
Принцип комбинированного регулирования сочетает принцип регулирования по отклонению и по возмущению.
В комбинированных системах принцип по отклонению реализуется с помощью главной обратной связи, а принцип регулирования по возмущению - с помощью связи по возмущению.