ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 33
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для того, чтобы нам проверить гипотезу потребуется осуществить это с помощью статистического критерия. Статистический критерий- случайная величина, которая служит для проверки нулевой гипотезы.
Поэтому, нужно определить нулевую и альтернативную гипотезы для заданной выборки.
Нулевая гипотеза (Ho): «О нормальном распределении генеральной совокупности баллов, по предмету «Литературы» студентов 1 курса (заочной формы обучения), факультета русской филологии и культуры».
Альтернативная гипотеза (H1): «О ненормальном распределении генеральной совокупности баллов, по предмету «Литературы» студентов 1 курса (заочной формы обучения), факультета русской филологии и культуры».
Используем критерий Пирсона, чтобы проверить, согласуется ли гипотеза с нормальным распределением генеральной совокупности X с заданным эмпирическим распределением.
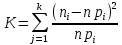
гдеs = 8.085,
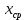= 61Теоретическая (ожидаемая) частота равна
= 
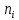, где n = 22Вероятность попадания в i-й интервал:
= Ф(x2) - Ф(x1)| Xi-Xi+1 | X* | ni | хi ni | S(Накопленная частота) | |x-xср|·ni | (x-xср)2·ni | Относительная частота, ni/n |
| 40-47 | 43,5 | 1 | 43.5 | 1 | 17,364 | 301,496 | 0,0455 |
| 47-54 | 52 | 4 | 208 | 5 | 35,455 | 314,256 | 0,182 |
| 54-61 | 57,5 | 7 | 402.5 | 12 | 23,545 | 79,198 | 0,318 |
| 61-68 | 64,5 | 5 | 322.5 | 17 | 18,182 | 66,116 | 0,277 |
| 68-77 | 72,5 | 5 | 362.5 | 22 | 58,182 | 677,025 | 0,277 |
| Σ | 22 | 1339 | | 152,727 | 1438,091 | 0 | |
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
Несмещенная оценка дисперсии - состоятельная оценка дисперсии/
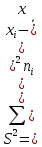=68.481Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 61 в среднем на 8.085
Оценка среднеквадратического отклонения.
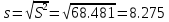
| xi÷xi+1 | ni | x1 = (xi - xср)/s | x2 = (xi+1 - xср)/s | Ф(x1) | Ф(x2) | pi=Ф(x2)-Ф(x1) | Ожидаемая частота, 22pi | Слагаемые статистики Пирсона, Ki |
| 40-47 | 1 | -2.5212 | -1.6753 | -0.4945 | -0.4535 | 0.041 | 0.902 | 0.01065 |
| 47-54 | 4 | -1.6753 | -0.4669 | -0.4535 | -0.1808 | 0.2727 | 5.9994 | 0.6663 |
| 54-61 | 7 | -0.8294 | 0.01648 | -0.2967 | 0.008 | 0.3047 | 6.7034 | 0.01312 |
| 61-68 | 5 | 0.01648 | 0.8624 | 0.008 | 0.3078 | 0.2998 | 6.5956 | 0.386 |
| 68-77 | 5 | 0.8624 | 1.9499 | 0.3078 | 0.4744 | 0.1666 | 3.6652 | 0.4861 |
| Σ | 22 | | | | | | | 1.5622 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения χ2 и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = χ2(5-2-1;0.05) = 5.99146; Kнабл = 1.56
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью показателей As и Ex.
В случае нормального распределения справедливо следующее условие: |As| < 3SAs; |A| < 3SAs; |E| < 3SEx
Проверим выполнение этого условия для нашего примера.
SAs=0.6124, SEx=0.5
As=-0.0145, Ex=-0.78
|-0.0145| < 3*0.6124=1.8371
|-0.78| < 3*0.5=1.5
Условия выполняются.
Проверку выборочной совокупности на близость ее к нормальному распределению можно производить, используя статистики χ2, As и Ex.
Сначала вычисляют статистику χ2 по формуле:
Затем при заданном уровне значимости α и числе степеней свободы k = 2 (используют в расчетах две статистики As и Ex) для распределения χ2 Пирсона находят χкр2. Если выполняется неравенство χ2 < χкр2, то гипотезу о нормальном распределении выборочной совокупности принимают. В противном случае, т.е. когда χ2>χкр2, гипотезу о нормальном распределении выборки отвергают.
Проверим гипотезу о том, что Х распределено по нормальному закону с помощью правила 3-х сигм.
Если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднеквадратического отклонения, т.е. все значения случайной величины должны попасть в интервал:
(x-3·σ ; x+3·σ)
В нашем случае этот интервал составит:
(61-3*8.085;61-3*8.085) = (36.745;85.255)
Все значения величин попадают в интервал, так как xmin=40; xmax=77
Из этого следует вывод, что: Каждое значение ряда отличается от среднего значения 61 в среднем на 8.085.Проверка гипотезы по критерию согласия Пирсона показала, что нет оснований отвергать гипотезу о нормальном законе распределения.
Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению.