9	6	1
А	Б	В

Задача 4Кручение круглого брусаДля вала круглого сечения заданной схемы (рис.1) требуется:1. Построить эпюру крутящих моментов. 2. Подобрать диаметр вала из условия прочности при заданном значении допускаемого напряжения [τ] и из условия жесткости при заданном значении допускаемого относительного угла закручивания []. Из полученных двух значений диаметра назначить больший.3. Построить эпюру максимальных касательных напряжений.4. Приняв модуль сдвига 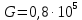МПа, построить эпюру углов поворота сечений по длине вала.5. Вычислить потенциальную энергию упругой деформации вала W и работу внешних сил А. 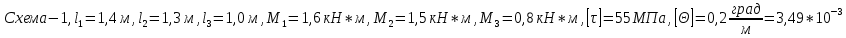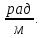При расхождении этих величин более 1 % следует уточнить расчет или найти ошибки.Дано: М₁М₂М₃l₁l₂l₃РешениеОпределим реакцию – момент М_А в заделке (рис. 1,а). Из условия равновесия вала М_А – М₁ – М₂ + М₃ = 0,

---

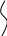
определим реактивный моментМ_А = М₁ + М₂ – М₃ = 1,6 + 1,5 – 0,8 = 2,3 кНм.М_А = 2,3 кНм М₁ = 1,6 кНм М₂ = 1,5 кНм М₃ = 0,8 кНм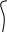а) 0 1 2 3М_А IIIIIIl₁ = 1,4 м l₂ = 1,3 м l₃ = 1,0 м 2,3 2,3 0,7 0,7 M_к, кН_*м

---

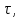
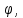
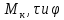
13,4 13,4 0,8 0,8 4,07 4,07 МПа4,65 4,65 0,0063 0,0051 0,0049 рад.Рис. 1. Эпюры Слева от сечения, проведенного на первом участке, действует только один реактивный момент М_А, причем, если смотреть на вал слева, он поворачивает рассматриваемую часть против часовой стрелки. Следовательно, на участке IМ_к1 = М_А = 2,3 кНм.По аналогии получаем:– на участке IIМ_к2 = М_А - М₁ = 2,3 - 1,6 = 0,7 кНм;– на участке III М_к3 = - М₃ = - 0,8 кНм.Строим эпюру крутящих моментов (рис. 1,б).Максимальный по модулю крутящий момент M

---

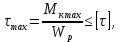
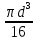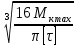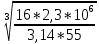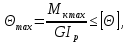
_{к max}= 2,3 кНм.Подбираем диаметр вала из условий прочности и жесткости.Условие прочности при кручениигде W_p – полярный момент сопротивления поперечного сечения. Для вала круглого сечения W_p = . 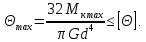С учетом этого условие прочности запишется в видеτ_max = ≤ [τ],откуда d ≥ = = 59,7 мм = 5,97 см.Условие жесткости при кручении валагде I_p – полярный момент инерции поперечного сечения.Так как для круглого сечения I_p = π d⁴/32, то условие жесткости имеет вид Следовательно, диаметр валаd≥ = 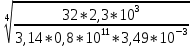= 0,0957 м = 9,57 см.Так как диаметр вала должен удовлетворять обоим условиям, окончательно принимаем d = 9,57 см.Определим максимальные касательные напряжения в поперечных сечениях вала.Вычислив предварительно полярный момент сопротивления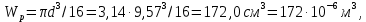находим:– участок I– 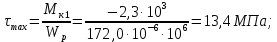участокII– 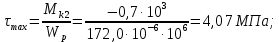участок III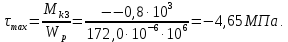Строим эпюру τ_max (рис. 1,в).Для построения эпюры углов поворота сечений сначала необходимо вычислить углы закручивания каждого из участков вала.Вычислив предварительно полярный момент инерции сеченияI_p = π d⁴ / 32 = 3,14 · 9,57⁴ / 32 = 823,1 см⁴ = 823,1٠10^-8 м⁴,получим:– участок I

---

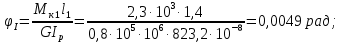
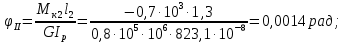
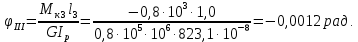
–участок II– участок IIIОбозначим характерные сечения вала, начиная от заделки, цифрами 0, 1, 2, 3 (рис. 1а). Очевидно, что в заделке сечение и после приложения заданных крутящих моментов остается неподвижным, т. е. φ₀ = 0.Углы поворота других характерных сечений находим алгебраическим суммированием углов закручивания отдельных участков:– сечения 1 φ₁ = φ_I= 0,0049 рад;– сечения 2 φ₂ = φ₁ + φ_II = 0,0049 + 0,0014 = 0,0063 рад;– сечения 3 φ₃ = φ₂ + φ_III= 0,0063 - 0,0012 = 0,0051 рад.Эпюра углов поворота сечений по длине вала показана на рис. 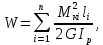1г.Вычислим потенциальную энергию упругой деформации вала Wи работу внешних сил А.Потенциальная энергия упругой деформациигде n = 3 – количество участков вала. 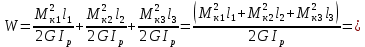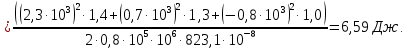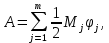Работа внешних силгде φ_j– угол поворота сечения, в котором приложен крутящий момент M_j;m = 3 – число моментов(реактивный момент М_А работы не совершает, так как сечение в заделке неподвижно (φ₀ = 0)).Все сечения вала после его нагружения повернулись (при наблюдении вала справа) по ходу часовой стрелки. 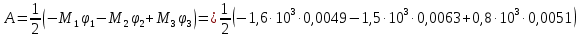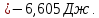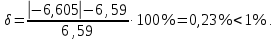В связи с этим работа моментов М₁и М₂, которые действуют в противоположном направлении, будет отрицательной, а работа момента М₃, действующего в обратном направлении – положительной.Следовательно,Расхождение величин W и АПрактически одинаковые значения энергии деформации и работы внешних сил свидетельствуют о том, что задача решена верно.

---

Смотрите также файлы

• Доклад Где применяются профстандарты.docx

• Задание Разработать и описать технологию эффективного найма психологапедагога, менеджера, руководителя (начальника) отдела (компании) по выбору.docx

• Отчет по производственной практике пп 01. 01 Информационные системы.ppt

• 2022 год план.docx

• Участие России в международном и олимпийском движении Студент группы С22Слс.pptx