Файл: Расчетнопроектировочная работа 1.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 06.11.2023

Просмотров: 47

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Астраханский государственный технический университет.

Расчетно-проектировочная работа №1


Расчётстатическиопределимоймногопролетнойбалкиот неподвижной нагрузки

Вариант№8/1. Выполнил :



Группа:ДССПБ21 Проверил(а)




Астрахань2023
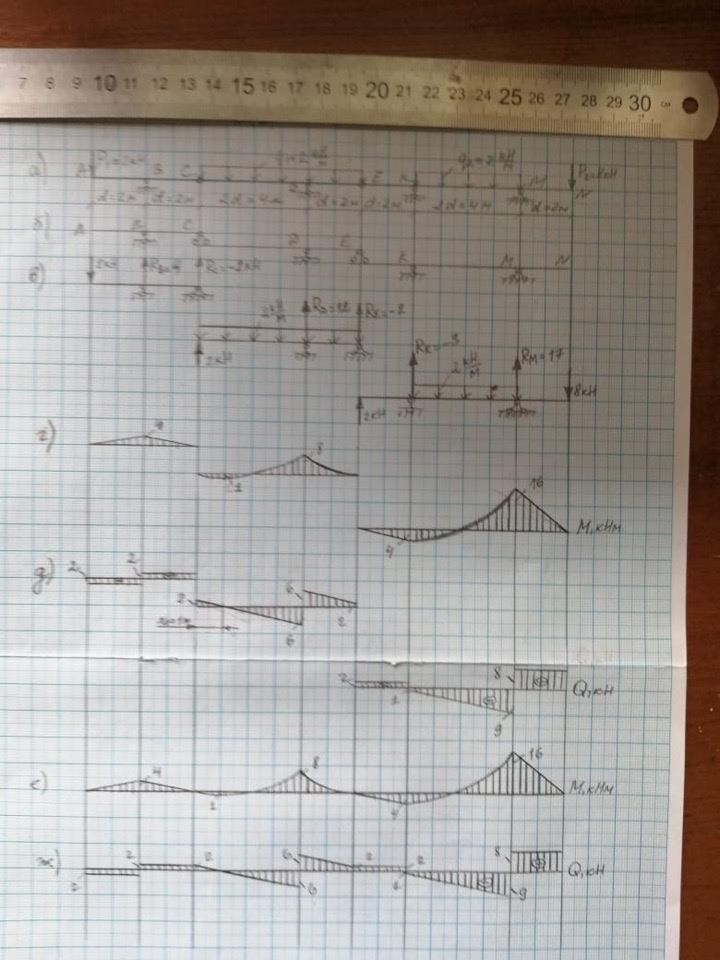
Дано:Р1= 2кН, Р2=8, кН, q1= 2кН/м, q2= 2кН/м,d= 2мРешение:

  1. Проверка геометрической неизменяемости системы

Многопролетнаястатическиопределимаябалка(риса)состоитизтрехбалок(дисков), соединенных между собой шарнирами С и Е, и имеет 5 опорных стержней. Число степеней свободы рассматриваемой системы определим по формуле, см.[2] п 1.3:где D=3–количестводисков; Ш = 2 – количество шарниров;С0=5–количествоопор.Степеньгеометрическойизменяемостиплоскойжесткойсистемы,тоестьобщеечисло степеней свободы системы с жесткими элементами и связями определяется как разность числа уравнений равновесия плоской системы, состоящей из D жестких дисков, равное 3D, и числа уравнений равновесия, составленных для каждой элементарной связи,число которых в плоской жесткой системе равно С.Этоположениеможновыразитьформулой,см.[2]п.1.4:где D=3–количестводисковвсистеме; С =9–числоэлементарныхсвязейсистемы.Тоестьрассматриваемаястатически
определимаябалкаимеетнеобходимое количество связей и представляет собой геометрически неизменяемую систему.Геометрическуюнеизменяемостьбалкиможноустановитьидругимспособом, составив поэтажную схему многопролетной балки (рис.б).Изпоэтажнойсхемымногоопорнойбалкивидно,чтодвухопорнаядвухконсольная балка EKMN с опорами K и M соединена с основанием тремя непараллельными и непересекающимисяводнойточкеопорнымистержнямиипоэтому–геометрически неизменяема, и может быть названа основной (рис. б).БалкиАBCиCDE,расположенныеэтажомвыше(рис.б),являютсявторостепенными или присоединенными.Такимобразом,многопролетнаястатическиопределимаябалка,представленнаяна рис. а, является геометрически неизменяемой.
  1. Построение эпюр изгибающих моментов М и поперечных сил Q от заданной неподвижной нагрузки
ДляпостроенияэпюризгибающихмоментовМипоперечныхсилQдлямногопролетнойстатическиопределимойбалкинеобходимоотдельнопостроитьэпюрыдля каждой балки (основной и присоединенных), а затем их совместить. Расчетные схемы этих балок представлены на рис. в, г и д. При этом построение эпюр изгибающих моментов ипоперечныхсилследуетвначалепроводитьдляприсоединенныхбалок,азатемдляосновной балки.

    1. Построение эпюр М и Q для присоединенной балки АВС

∑MB= 0; 2

+ RC

= 0; RC = -2кН

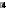∑MС= 0; 2

  • RB

= 0; RB = 4кН


Участок 1 0 x2 м
∑Fy= 0; -2 – Q= 0; Q= -2 кН
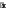ΣM= 0; M+ 2 x= 0; M= -2
при х= 0 M= 0
при х= 2м M= -4 кНм Участок 2 0 x2 м

∑Fy= 0; Q– 2 = 0; Q= 2 кН
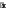ΣM= 0; -M- 2 x= 0; M= -2
при х= 0 M= 0
при х= 2м M= -4 кНм

    1. Построение эпюр М и Q для присоединенной балки СDE




∑MD= 0; -2

+ 2 4 4/2 – 2 2 2/2 + RE

= 0; RE = -2кН

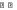
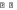
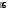∑ME= 0; -2

+ 2 6 6/2 – RD

= 0; RD = 12кН


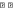
Участок 1 0 x4 м
∑Fy= 0; 2 – 2x– Q= 0; Q= 2 – 2x
при х= 0 Q= 2кН
при х= 4м Q= -6 кН
точка пересечения: х0 = 1м
ΣM= 0; M– 2 x+ 2xх/2 = 0; M= 2 x–x2
при х= 0 M= 0
при х = 4м M = -8 кНм прих0=1мM=1кНм Участок 2 0x2 м∑Fy=0; Q–2–2x= 0;Q= 2+ 2xпри х = 0 Q = 2кН прих=2мQ=6кНΣM= 0;-M–2x– 2xх/2= 0;M=–2x– x2прих= 0M= 0прих= 2мM= -8кНм

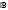
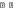
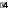    1. Построение эпюр М и Q для основной двухконсольной балки EKMN

∑MK= 0; -2

- 8

  • 2 4 4/2 + RM

= 0; RM = 17кН

∑ME= 0; -8

+ 2 4 4/2 – 2

  • RK

= 0; RK = -3кН


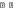
Участок 1 0 x2 м
∑Fy= 0; 2 – Q= 0; Q= 2 кН
ΣM= 0; M- 2 x= 0; M= 2
при х= 0 M= 0
при х= 2м M= 4 кНм Участок 2 0 x4 м

∑Fy= 0; –Q+ 2 – 3 – 2x= 0; Q= -1 – 2x
при х = 0 Q = -1кН при х= 4м Q= -9кН

ΣM= 0; M– 2(2+x) + 3x+ 2xх/2 = 0; M= 4 - x–x2
при х= 0 M= 4 кНм
при х= 4м M= -16 кНм
Участок30 x2м∑Fy=0; Q–8=0; Q=8кНΣM= 0;–M– 8x= 0;M=-8прих= 0M= 0при х= 2мM= -16кНмСовмещаемотдельнопостроенныеэпюрыQи M (рис.е,ж)Делаемпроверкуправильностиопределенияреакцийдлявсеймногопролетнойбалки.∑Fy=0;RB+RD+RK+RM–2–8–26–2 =4+12–3+17–2–8–12–8= 0

Смотрите также файлы