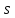Файл: Контрольная работа Вариант 3 Фамилия Чудинов Имя Кирилл Отчество.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 36
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
Дисциплина: Дискретная математика
Контрольная работа
Вариант 3
Фамилия:___Чудинов____
Имя:___Кирилл____
Отчество:_Витальевич__
Группа №:____РБ-11з______
Проверил:______________
Санкт-Петербург
2023
Задание 1
Используя правила Моргана получить ДНФ функции
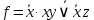 и упростить полученную ДНФf.
и упростить полученную ДНФf.Решение
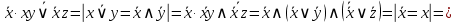
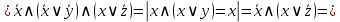
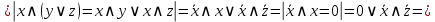
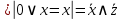
Задание 2
Даны две функции f1 (x, y), f2 (x, y, z). Требуется:
а) для функции f1 (x, y) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. Упростить, если возможно, СДНФ.
б) для функции f2 (x, y, z) составить таблицу истинности и найти по ней полином Жегалкина, СДНФ и СКНФ. По карте Карно получить минимальную ДНФ, нарисовать эквивалентную РКС.
в) составить таблицу Поста для системы функций f1 (x, y), f2 (x, y, z), проверить полноту системы и выбрать базисы, если она полная.
Решение
а)
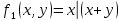
Составим таблицу истинности:
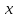 | 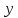 | 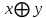 | 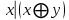 | Коэффициенты полинома Жегалкина | |
| 1 | 1 | 0 | 1 | 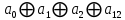 | 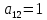 |
| 1 | 0 | 1 | 0 | 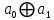 | 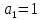 |
| 0 | 1 | 1 | 1 | 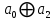 | 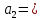 0 0 |
| 0 | 0 | 0 | 1 | 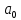 | 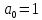 |
Составим
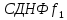 по наборам для которых
по наборам для которых 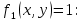
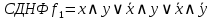
Упростим СДНФ
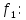
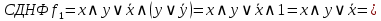
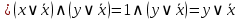
Составим
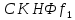 по наборам для которых
по наборам для которых 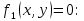
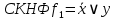
Составим полином Жегалкина:
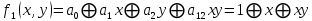
б)
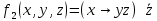
Составим таблицу истинности:
 |  | 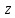 | 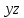 | 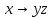 | 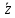 | 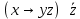 | Коэффициенты полинома Жегалкина | |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 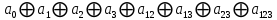 | 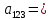 0 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 |  | 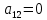 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 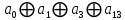 | 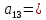 0 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |  |  |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 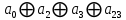 | 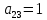 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |  | 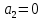 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 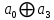 | 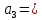 1 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |  |  |
Составим
 по наборам для которых
по наборам для которых 
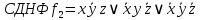
Составим
 по наборам для которых
по наборам для которых 
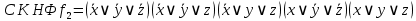
Составим полином Жегалкина:
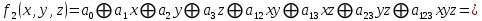
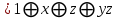
Заполним карту Карно:

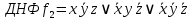
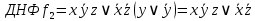
Составим РКС:
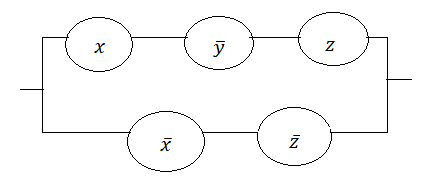
Таблица Поста имеет вид:
| Функция | 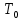 | 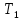 | S | M | L |
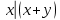 | - | + | - | - | - |
 | - | - | - | - | - |
Так как:
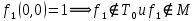
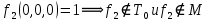
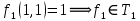
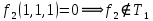
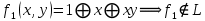 , не линейная, содержит
, не линейная, содержит 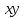
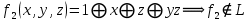 , не линейная, содержит
, не линейная, содержит 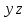
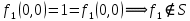
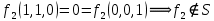
Система функций полная, т.к. в таблице Поста нет столбца из одних «+». Проверяем на полноту каждую функцию:
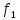 - не составляет полной системы, т.к. нет функции не входящей в классы
- не составляет полной системы, т.к. нет функции не входящей в классы 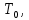 L, M и S.
L, M и S.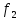 - образует полную систему и является базисом. Других базисов нет.
- образует полную систему и является базисом. Других базисов нет.Задание 3
Задан граф:
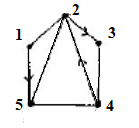
Составить для данного графа структурную матрицу. Найти:
а) все простые пути из вершины
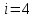 в вершину
в вершину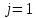 ;
;б) совокупность всех сечений между вершинами
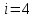 и
и 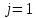 .
.Решение
Структурная матрица имеет вид:
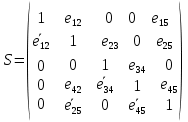
Из структурной матрицы S, а затем вычеркнем из неё 1-ю строчку и 4-й столбец, тем самым получив минор M14. Согласно теореме разложения определитель равен дизъюнкции (сумме) произведений элементов любой строки (или столбца), умноженных на свои алгебраические дополнения (в данном случае миноры).
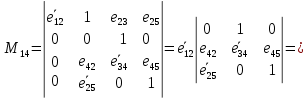
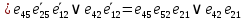
Использованные при упрощении свойства:
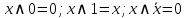
При записи ответа рёбра идут в порядке прохождения вершин от
 и
и  .
.Для нахождения сечений между вершинами
 и
и 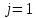 . заменим дизъюнкцию на конъюнкцию, а конъюнкцию на дизъюнкцию и раскроем скобки.
. заменим дизъюнкцию на конъюнкцию, а конъюнкцию на дизъюнкцию и раскроем скобки.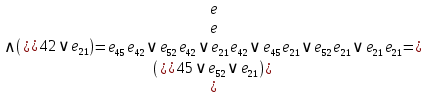
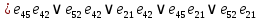
Задание 4
Задана сеть
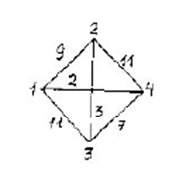
и начальный поток f.
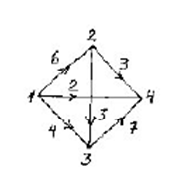
Требуется построить максимальный поток, считая вершину с номером 1 источником и вершину с номером 4 стоком. Указать минимальное сечение, величина которого равна максимальному потоку.
Решение
Поток fиз
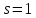 в
в 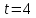 имеет величину
имеет величину 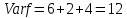
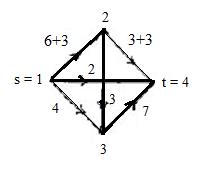
Путь из
 в
в  :
: 
Пометки вершин:
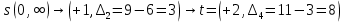
Добавка к потоку:
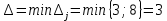
Строим новый поток
 :
: 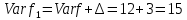
Путь из s в t, на котором возможно увеличение потока не построить, поскольку невозможно дойти до стока. Значит поток
 , построенный на основе заданного в условии, максимален:
, построенный на основе заданного в условии, максимален: 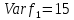 .
.Помеченная вершина:
 = {1}.
= {1}.Непомеченные вершины:
 = {3,2,4}.
= {3,2,4}.Построим начальный поток иначе:
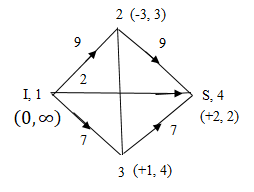
Поток fиз
 в
в 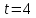 имеет величину
имеет величину 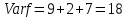
Путь из