Файл: Отчет по лабораторной работе 6 Определение момента инерции твердого тела.docx
Добавлен: 06.11.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 |
| МИНОБРНАУКИ РОССИИ |
Федеральное государственное бюджетное образовательное учреждениевысшего образования«МИРЭА - Российский технологический университет»РТУ МИРЭА |
Филиал РТУ МИРЭА в г. Фрязино
Кафедра общенаучных дисциплин
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №__6__
«Определение момента инерции твердого тела»
по дисциплине
«Физика»
Выполнил студент группы Ф???-??-?? Аноним А.А.
(учебная группа)
Принял
Кандидат физико-математических наук Белихов А.Б.
Лабораторные работы выполнены «??» ?? 20??г.
(подпись студента)
«Зачтено»
«??» ?? 20??г.
(подпись руководителя)
Фрязино 20??
Цель: научиться определять момент инерции твердого тела
Оборудование: маховик со шкивом, кронциркуль, грузы с нитью, секундомер, линейка с погрешностью 0.5мм
Ход работы:
Опыт №1
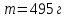
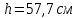
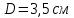
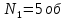
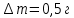
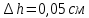
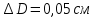
| Опыт 1 | ||||||
| № | t, сек | Δt | (Δt)2 | 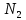 | ΔN2 | (ΔN2)2 |
| 1 | 15,42 | 0,14 | 0,0196 | 8,2 | 0,16 | 0,0256 |
| 2 | 15,10 | 0,18 | 0,0324 | 7,75 | 0,29 | 0,0841 |
| 3 | 15,34 | 0,06 | 0,0036 | 8,25 | 0,21 | 0,0441 |
| 4 | 15,08 | 0,2 | 0,04 | 8,1 | 0,06 | 0,0036 |
| 5 | 15,43 | 0,15 | 0,0225 | 7,9 | 0,14 | 0,0196 |
| | 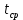 =15,28 =15,28 | | | 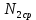 =8,04 =8,04 | | |
Вычисляем среднее значение момента инерции J по формуле (1):
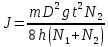
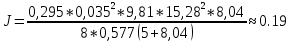 кг*
кг*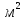
Находим абсолютную погрешность измерения момента инерции ∆J. Для этой цели вычисляем относительную погрешность:
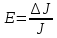
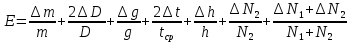 (2)
(2)Погрешностью
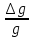 можно пренебречь, так как она мала по сравнению с остальными погрешностями. Погрешность
можно пренебречь, так как она мала по сравнению с остальными погрешностями. Погрешность 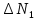 очень невелика, можно считать
очень невелика, можно считать 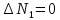 . Тогда последние два члена выражения (2) можно переписать так:
. Тогда последние два члена выражения (2) можно переписать так: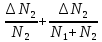 (3)
(3)Необходимо обратить внимание на то, что
 входит в выражение (1) как в числитель, так и в знаменатель. Знак погрешности
входит в выражение (1) как в числитель, так и в знаменатель. Знак погрешности 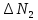 нам неизвестен; но он будет один и тот же как в числителе, так и в знаменателе. Допустим, что
нам неизвестен; но он будет один и тот же как в числителе, так и в знаменателе. Допустим, что 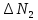 имеет знак плюс; тогда величина, вычисленная по формуле (1), из-за присутствия
имеет знак плюс; тогда величина, вычисленная по формуле (1), из-за присутствия 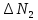 в числителе будет получена увеличенной по сравнению с истинным её значением. Но наличие
в числителе будет получена увеличенной по сравнению с истинным её значением. Но наличие 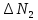 в знаменателе с тем же знаком уменьшает значение J. Следовательно, эти погрешности отчасти компенсируются. Математически мы можем учесть это, беря второй член выражения (3) со знаком минус, т.е. надо рассмотреть:
в знаменателе с тем же знаком уменьшает значение J. Следовательно, эти погрешности отчасти компенсируются. Математически мы можем учесть это, беря второй член выражения (3) со знаком минус, т.е. надо рассмотреть: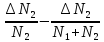 (4)
(4)Так как обычно
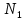 мало по сравнению с
мало по сравнению с  , то
, то
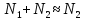
Тогда выражение (4) можно считать равным нулю:
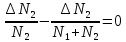
Учтя все эти замечания, для относительной погрешности E будем иметь более простое выражение:
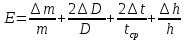
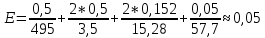
Вычислив относительную погрешность, находим:
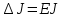
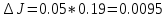
Конечный результат:
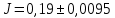 кг*
кг* =
= 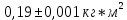
Опыт №2
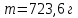
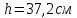





| Опыт 2 | ||||||
| № | t, сек | Δt | (Δt)2 |  | ΔN2 | (ΔN2)2 |
| 1 | 11,4 | 0,40 | 0,16 | 13,25 | 0,36 | 0,1296 |
| 2 | 12 | 0,20 | 0,04 | 12,75 | 0,14 | 0,0196 |
| 3 | 11,72 | 0,08 | 0,0064 | 12,65 | 0,24 | 0,0576 |
| 4 | 12,15 | 0,35 | 0,1225 | 13 | 0,11 | 0,0121 |
| 5 | 11,75 | 0,05 | 0,0025 | 12,9 | 0,01 | 0,0001 |
| |  =11,80 =11,80 | | | 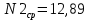 | | |
Вычисляем среднее значение момента инерции J по формуле (1):

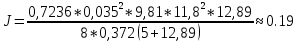 кг*
кг*
Находим абсолютную погрешность измерения момента инерции ∆J. Для этой цели вычисляем относительную погрешность:

 (2)
(2)Погрешностью
 можно пренебречь, так как она мала по сравнению с остальными погрешностями. Погрешность
можно пренебречь, так как она мала по сравнению с остальными погрешностями. Погрешность  очень невелика, можно считать
очень невелика, можно считать  . Тогда последние два члена выражения (2) можно переписать так:
. Тогда последние два члена выражения (2) можно переписать так: (3)
(3)Необходимо обратить внимание на то, что
 входит в выражение (1) как в числитель, так и в знаменатель. Знак погрешности
входит в выражение (1) как в числитель, так и в знаменатель. Знак погрешности  нам неизвестен; но он будет один и тот же как в числителе, так и в знаменателе. Допустим, что
нам неизвестен; но он будет один и тот же как в числителе, так и в знаменателе. Допустим, что  имеет знак плюс; тогда величина, вычисленная по формуле (1), из-за присутствия
имеет знак плюс; тогда величина, вычисленная по формуле (1), из-за присутствия  в числителе будет получена увеличенной по сравнению с истинным её значением. Но наличие
в числителе будет получена увеличенной по сравнению с истинным её значением. Но наличие  в знаменателе с тем же знаком уменьшает значение J. Следовательно, эти погрешности отчасти компенсируются. Математически мы можем учесть это, беря второй член выражения (3) со знаком минус, т.е. надо рассмотреть:
в знаменателе с тем же знаком уменьшает значение J. Следовательно, эти погрешности отчасти компенсируются. Математически мы можем учесть это, беря второй член выражения (3) со знаком минус, т.е. надо рассмотреть: (4)
(4)Так как обычно
 мало по сравнению с
мало по сравнению с  , то
, то
Тогда выражение (4) можно считать равным нулю:

Учтя все эти замечания, для относительной погрешности
E будем иметь более простое выражение:

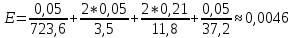
Вычислив относительную погрешность, находим:

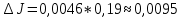
Конечный результат:
 кг*
кг*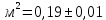 кг*
кг*
Вывод: так как два опыта с разными грузами и высотой практически равны, можно считать, что определение момента инерции твердого тела прошло успешно
Задача из задачника Иродова
Задача 1.238
Условие:
Диаметр диска d=20 см, масса m=800 г. Определить момент инерции J диска относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска.
 Дано: Решение:
Дано: Решение:d = 0,2м
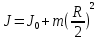 ,
, 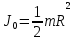
m = 0,8кг
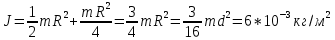
J - ?
Ответ: