Файл: Аксиома 2 аксиома эквивалентности системы сил.docx

1. 
   Основные понятия и определения. Аксиомы статики и их следствия. Виды связей и их реакции
   

Понятия: Теоретическая механика – это наука о наиболее общих законах механического движения и механического взаимодействия.

Механическое движение – изменение с течением времени взаимного положения в пространстве материальных тел. Или изменение взаимного положения.

Материальная точка– это точка обладающая массой, ей может считаться любое материальное тело если его размерами в данной задаче можно пренебречь.

Абсолютно твёрдое тело – такое материальное тело расстояние между двумя точками которого всегда остается неизменным.

Статика – это раздел механики в котором изучается условия равновесия механических систем под воздействием силы, также она рассматривает законы по которым системы сил могут при образовываться.

Кинематика – (движение) – это раздел механики в котором изучаются движения материальных тел без учёта определяющих его сил и масс то есть как движение чисто геометрических объектов

Динамика (сила) – это раздел механики в котором изучается движение механических систем под действием сил, она является Синтезом статики и кинематики.

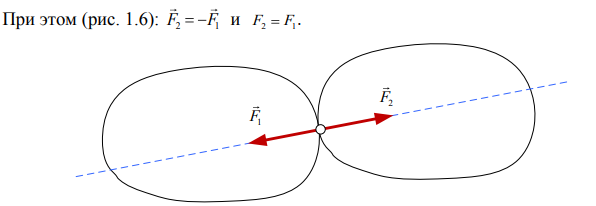
Аксиома №1. Аксиома двух сил – система из двух сил – является уравновешенной тогда и только тогда, когда эти силы: 1. Имеет общую линию действия. 2.Направленный по ней в противоположные стороны. 3. Равны по модулю

С
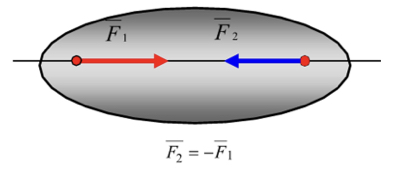
ледствие: если для некоторых системы сил существует эквивалентная ей равнодействующая, то данная система сил может быть уравновешено одной силой, которая называется уравновешивающий силой.
Аксиома №2: аксиома эквивалентности системы сил.

Две системы сил отличающиеся друг от друга на уравновешенную систему сил эквивалентны. Это значит, что к любой системе сил можно добавить или из нее исключить уравновешенную систему сил. Действие системы сил на тело при этом не изменится.

Следствие 1: силу можно переносить вдоль линии действия в другую точку данного тела.

Это аксиома справедлива при рассмотрении абсолютно твёрдых тел в этом случае сила может рассматриваться как скользящий вектор он не связан с конкретной точкой приложения на линии её действия.

---

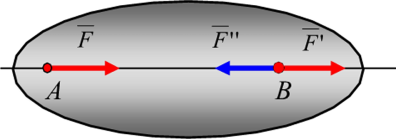
Произвольной точке B на линии действия силы добавляем уравновешивающие силу и получаем систему сил.

F’=F’’. F’’= -F

Аксиома №3: аксиома параллелограмма сил. Система из двух сил, приложенных в одной точке, имеет равнодействующую, равную их векторной сумме, и приложенную в той же точке



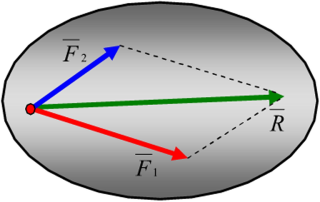
R=F1+F2

Геометрическая сумма двух сил F1 и F2 изображается диагональю параллелограмма построенного на этих силах как на его сторонах.


Следствие: любую силу можно разложить на две непараллельные силы приложенные в той же точке, что и исходная сила.



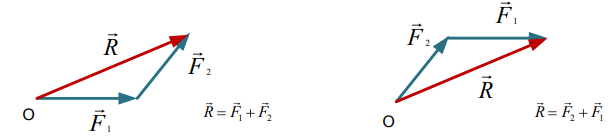
Таким образом если линии действия двух сил пересекаются то эти силы имеют равнодействующую . Если же линия действия сил не пересекаются то эти силы не могут иметь равнодействующей.
Аксиома №4: Аксиома двух тел

Принцип равенства действия и противодействия: При всяком действии одного тела на другое силы их взаимодействия: 1) имеют общую линию действия, 2) направлены по ней в противоположные стороны и 3) равны по модулю.



Свойство внутренних сил: Векторная сумма внутренних сил любой механической системы всегда равна нулю.
Аксиома №5: Принцип отвердевания

Равновесие изменяемого (деформируемого) тела не нарушится, если оно станет абсолютно твердым.

Приведенный принцип позволяет при составлении уравнений статики для деформируемого тела, находящегося в равновесии, считать его абсолютно твердым
2. Система сходящихся сил. Теорема о равнодействующей системы

сходящихся сил.
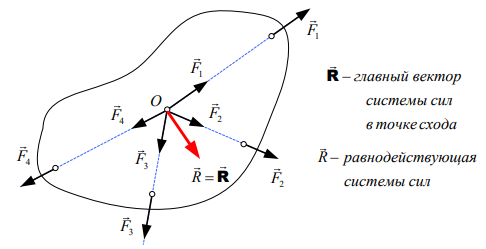
Сходящейся системой сил называются совокупность сил, линии действия которых пересекаются в одной точке − точке схода.

Система сходящихся сил имеет равнодействующую, приложенную в точке пересечения линий действия сил, которая геометрически равна главному вектору этой системы сил.

Главный вектор можно найти для любой системы сил. Если привязать его к точке схода системы, проведя через нее линию действия главного вектора, то полученная сила будет являться равнодействующей. Это характерно только для сходящихся систем сил. Для других систем сил равнодействующая может определяться иначе. Существуют системы сил, которые вообще не имеют равнодействующй, что означает, что такие системы сил невозможно заменить одной силой.

---

Отсюда следует, что проекции равнодействующей сходящейся системы сил определяются так же, как и проекции главного вектора:
3. Геометрический и аналитический способы сложения сил. Разложение сил.

Геометрический:

Вектор, равный векторной (геометрической) сумме сил системы будем называть главным вектором системы сил

Главный вектор, как геометрическая сумма всех сил системы, никак не связана с какой-то определенной точкой пространства. Можно сказать, что главный вектор можно определить в любой точке. Величина и направление главного вектора системы не зависит от положения точки приведения.








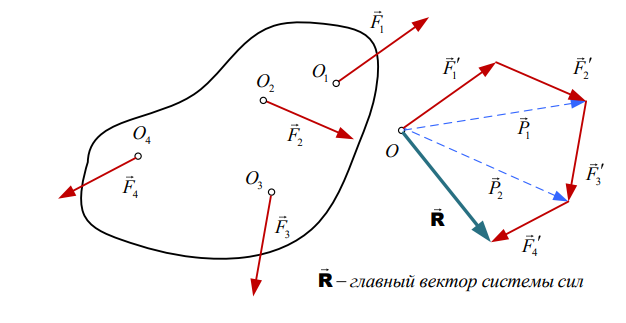
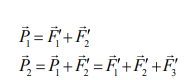
В случае плоской системы сил возможно графическое построение многоугольника сил в принятом масштабе сил, на чем основан графический метод решения задач теоретической механики. В пространственном случае графическое построение многоугольника сил невозможно Главный вектор не зависит от порядка суммирования векторов. Поскольку главный вектор не зависит ни от положения точки приведения ни от порядка суммирования векторов, его называют первым (или векторным) инвариантом системы сил.
Аналитический:

При аналитическом способе суммирования векторов используется известная из векторной алгебры теорема.

Проекция суммы векторов на ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.

Пусть необходимо найти главный вектор системы сил . Для этого необходимо выполнить сложение n сил, Поскольку равны векторы, стоящие в левой и правой частях последнего равенства, должны быть равны и их проекции на ось. Спроектируем это равенство на оси х, у, z:

---

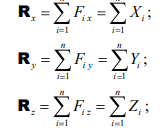
Главный вектор системы сил будет равен нулю в том случае, когда все три суммы проекций исходных сил будут равны нулю.


4. Условия и уравнения равновесия системы сходящихся сил. Теорема о трех силах.
Условия и уравнения равновесия системы сходящихся сил.

В общем случае сходящаяся система не является уравновешенной. Исключение составляет случай, когда равнодействующая, а следовательно и главный вектор этой системы сил равны нулю.

Для равновесия системы сходящихся сил, необходимо и достаточно, чтобы выполнялось одно из следующих условий:

1. В векторной форме: главный вектор системы сил должен быть равен нулю

2. В геометрической форме: силовой многоугольник должен быть замкнут.

3. В аналитической форме: сумма проекций сил на каждую из координатных осей должна быть равна нулю.

Для системы сходящихся сил в пространстве получаем три уравнения равновесия:



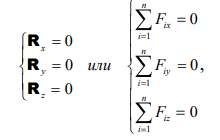
Теорема о трех силах

ТЕОРЕМА

Для равновесия твердого тела, находящегося под действием трех непараллельных сил, необходимо, чтобы линии их действия пересекались в одной точке.

Доказательство

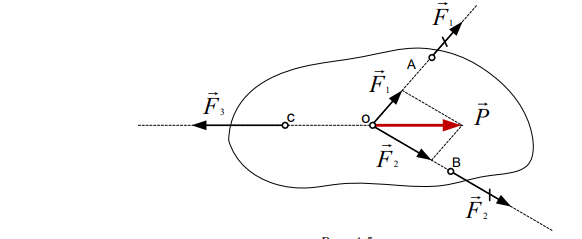
Пусть на тело действуют (рис. 4.5) три силы F1, F2,F3

Перенесем силы F1 F2 в точку пересечения линий действия и сложим их:



Тогда на тело будут действовать только две силы: P и F3. Под действием двух сил по I аксиоме тело может находиться в равновесии только когда силы P и F3 равны по величине, противоположно направлены и лежат на одной прямой. Отсюда следует необходимость пересечения линий действия трех сил в одной точке.



5. Момент силы относительно центра на плоскости. Главный вектор и главный момент плоской системы сил.

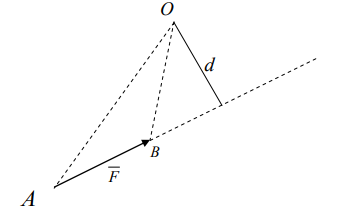
Определение: моментом силы относительно центра на плоскости называется взятое с соответствующим знаком произведение модуля силы на кратчайшее расстояние от центра до линии действия силы. Это кратчайшее расстояние от центра до линии действия силы называется плечом силы относительно центра.

---

Момент силы считается положительным, если сила вращает плоскость чертежа относительно центра против часовой стрелки, и отрицательным, если она вращает картинку чертежа относительно центра по часовой стрелке. Момент силы равен нулю, если линия действия силы пересекает центр (плечо силы равно нулю). Так, если AB – вектор силы F то M₀(F )=F*d.

Соединим концы вектора силы AB с центром О, тогда площадь треугольника следовательно, момент силы относительно центра на плоскости можно определить как



Главный вектор и главный момент плоской системы сил.

Главным моментом M_o системы сил относительно некоторой точки О (данного центра) называется векторная сумма моментов всех сил системы относительно этой точки:

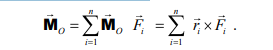
Плоской системой называется система сил, линии действия которых лежат в одной плоскости.



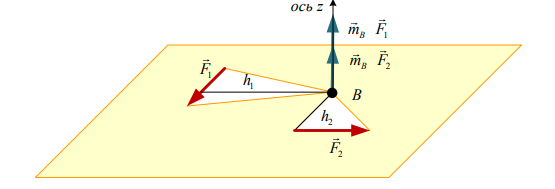
Из рис видно, что при расположении всех сил системы на одной плоскости вектора моментов сил системы относительно точек плоскости расположены к этой плоскости перпендикулярно. Все вектора моментов расположены параллельно друг другу и для указания их направления достаточно одного знака − знака проекции вектора на ось z, перепендикулярную к плоскости.

Величина момента равна произведению силы на плечо:

Если момент направлен против часовой стрелки − он считается положительным. При переходе к векторному представлению такое правило знаков соответствует знаку проекции вектор-момента на ось z. Сложив моменты всех сил системы относительно точки О, получим скалярную величину – главный алгебраический момент плоской системы сил относительно точки О:

---