Образец выполнения практического задания 1

Исходные данные: U = 16 кВ, x_m = 22 см, y_m = 16 см, r₀ = 12 мм, а = 28 см.

1. Построим расчетную схему.




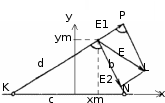
Рис. 2. Расчетная схема – двухпроводная линия

2. Из треугольника mX_mN (рис. 3 а) найдем расстояние b по формуле 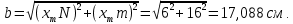(1):

(1)

3. Из треугольника КX_mm (рис. 3 б) найдем расстояние d по формуле 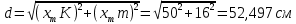(2):

. (2)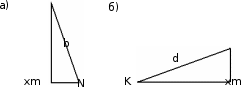




Рис. 3. Расчет геометрической модели
4. Напряженность электрического поля Е₁ от проводника +τ направлена вдоль отрезка, соединяющего точку +τ и точку m, и определяется по формуле 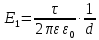(3):

. (3)

Напряженность электрического поля Е₂ от проводника –τ направлена вдоль отрезка, соединяющего точку –τ и точку m, и определяется по формуле 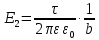(4):

. (4)

Треугольник mPL(см. рис. 2) подобен треугольнику KmN, так как отношение длин двух сторон одного треугольника (b/d) пропорционально отношению длин двух сторон другого треугольника (Е₁/Е₂). Следовательно, можно записать:

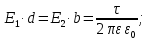(5)

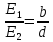. (6)

Заключенные между сторонами d и a и сторонами mP и PL углы равны, как углы между параллельными сторонами (см. рис. 2). Из подобия треугольников следует:

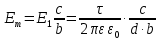, (7)

где E_m– напряженность электрического поля в точке m;

τ– линейная плотность электрического заряда, определяется далее по формуле (10);

ε– относительная диэлектрическая проницаемость среды, в которой находится точка m. Согласно исходным данным ε = 1;

ε₀ – электрическая постоянная (абсолютная диэлектрическая проницаемость вакуума). Принимаем ε₀ = 8,85·10^-12 Ф/м;

c, d, b – длины сторон треугольников (см. рис. 2).

---

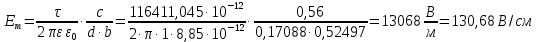. (8)

5. Определим погонную ёмкость заданной двухпроводной линии по формуле 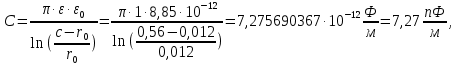(9):

(9)

где с – расстояние между проводами (расстояние между проводом +τ и проводом –τ). Согласно заданию 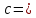28 + 28 = 56 см = 0,56 м;

r₀ – радиус провода (согласно заданию r₀= 12 мм = 0,012 м).

6. Используя известную формулу, связывающую между собой электрический заряд, напряжение и емкость, определим линейную плотность электрического заряда 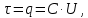(10):

(10)

где U = 16 кВ – напряжение, питающее линию (согласно исходным данным),



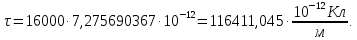
7. Определим потенциал в точке m по формуле 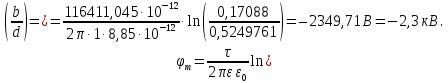(11):

(11)

Вывод: величина потенциала и напряженности в произвольной точке электростатического поля зависят от диэлектрической проницаемости среды и удаленности от линии.

---

Смотрите также файлы

• Коетрольная работа.docx

• Разведывательный анализ данных.docx

• Модернизация системы инженернотехнической защиты.docx

• Определение уранового эквивалента суммарного содержания естественнорадиоактивных элементов по данным интегрального гаммаметода.docx

• Методическая разработка для проведения практического занятия по пожарностроевой подготовке с личным составом 39 пч фпс тема занятия Боевое развёртывание с установкой переносного лафетного ствола время.doc