Статистически параметр потока отказов может быть определён по формуле:
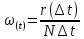, (6.1)
где 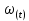– параметр потока отказов;

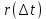– число отказов за наработку t + ;

N – количество объектов наблюдения;

– интервал наработки.
Найдём число отказов за наработку для каждого интервала по таблице 6.1:
; ; ; ;
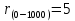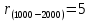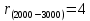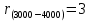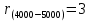
Определим параметр потока отказов для каждого интервала:
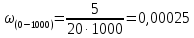(ч^-1)

(ч^-1)

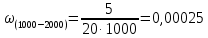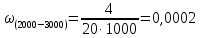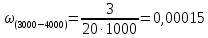(ч^-1)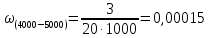

(ч^-1)

(ч^-1)

Статистически среднюю наработку на отказ можно определить по формуле:
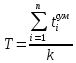, (6.2)
где Т – средняя наработка на отказ;

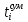– суммарная наработка до отказов за период наблюдений i-го объекта;

n – количество объектов, отказавших за период наблюдений;

k – суммарное число отказов объектов за период наблюдений.
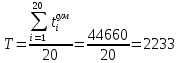(ч)
Коэффициент оперативной готовности можно определить по формуле:
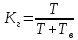, (6.3)
где 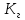– коэффициент готовности;

Т – средняя наработка на отказ;

Т_в– среднее время восстановления.

---

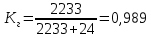
«Задание 7»
По приведенным в таблице данным определить вероятность безотказной работы и вероятность отказа, плотность распределения наработки до отказа на момент наработки t. Определить среднюю наработку до первого отказа. Надежность объекта подчиняется экспоненциальному закону распределения.
Таблица 7.1 – Расчёты по заданию 7

0 вариант	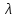, 1/км	t, км
	2,7 ∙ 10-5	2000

При принятии экспоненциального закона для описания надежности, предполагается, что изделие проходит период эксплуатации, когда постепенные отказы еще не проявились и надёжность характеризуется внезапными отказами с постоянной интенсивностью λ(t) = λ.

Вероятность безотказной работы за наработку t при принятии экспоненциального закона определяется по зависимости:
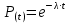, (7.1)
где – вероятность безотказной работы за наработку t;

λ – интенсивность отказов.


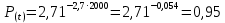
Вероятность отказа за наработку t определяется:
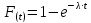, (7.2)
где – вероятность отказа за наработку t;

λ – интенсивность отказов.

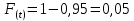
Плотность распределения наработки до отказа определяется:
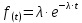, (7.3)
где 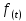– плотность вероятности отказов;

λ – интенсивность отказов.



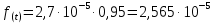
Средняя наработка до первого отказа определяется:
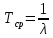, (7.4)
где – средняя наработка до отказа;

λ – интенсивность отказов.
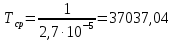(ч)
«Задание 8»
Объект состоит из 5 элементов, соединенных с точки зрения обеспечения надежности последовательно. Определить вероятность безотказной работы и вероятность отказа объекта, если вероятности отказа каждого элемента имеют значения, приведенные в таблице. Начертить схему соединения элементов.

---

Таблица 8.1 – Расчёты по заданию 8

0 вариант	P1(t)	P2(t)	P3(t)	P4(t)	P5(t)
	0,99	0,99	0,93	0,99	0,91

При последовательном соединении элементов вероятность безотказной работы всего объекта рассчитывается по формуле:
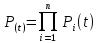, (8.1)
где – вероятность безотказной работы объекта за наработку t;

n – количество элементов в структуре объекта;

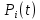– вероятность безотказной работы i-го элемента конструкции за наработку t.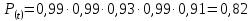

При последовательном соединении элементов вероятность отказа всего объекта рассчитывается:
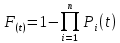, (8.2)
где – вероятность отказа объекта за наработку t;

n – количество элементов в структуре объекта;

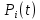– вероятность безотказной работы i-го элемента конструкции за наработку t.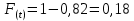








1

2

3

4

5

Рисунок 8.1 – Схема при последовательном соединении элементов
«Задание 9»
Определить вероятность безотказной работы и вероятность отказа объекта из задания 8, если 2, 3 и 4 элементы соединены параллельно. Начертить схему соединения элементов.

При параллельном соединении элементов конструкции вероятность безотказной работы всего объекта определяется:

---

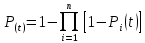, (9.1)
где – вероятность безотказной работы объекта за наработку t;

n – количество элементов в структуре объекта;

– вероятность безотказной работы i-го элемента конструкции за наработку t.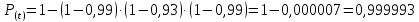

По формуле 8.1 найдём вероятность безотказной работы всего объекта:

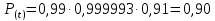
По формуле 8.2 найдём вероятность отказа всего объекта:





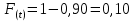
2





5

1

3



4

Рисунок 9.1 – Схема при смешанном соединении элементов
При соединении трёх элементов параллельно в схеме из пяти элементов надёжность увеличивается так как 0,18 > 0,10.

Список литературы
1. Надежность подвижного состава железнодорожного транспорта: учеб. пособие / В. В. Пигунов; М-во транспорта и коммуникаций Респ. Беларусь, Белорус. гос. ун-т трансп. – Гомель : БелГУТ, 2016. – 202 с

2. ГОСТ 27.002-2015. Надежность в технике. Термины и определения

3. ГОСТ Р 27.607-2013. Надежность в технике. Управление надежностью. Условия проведения испытаний на безотказность и статистические критерии и методы оценки их результатов

4. Р 50–109–89 Рекомендации. Надежность в технике. Обеспечение надежности изделий. Общие требования

---

Смотрите также файлы

• Возникновение юридического лица.docx

• Тестові завдання з навчальної дисципліни медична біологія до ліцензійного іспиту.doc

• "христианские принципи в песне кукла с человеческим лицом музыкальной группы пикник".docx

• Исполнение кадровых требований фгос.doc

• Правильные ответы на задания тестов 1 Вправе ли избиратель проголосовать за другого избирателя.pdf