ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 192
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практикум Excel, СПФ, ВМиКМ Осипов Е.И
Лабораторная работа № 10
Симплекс-метод
-
Цель работы.
Расширить и углубить практические знания и навыки в области применения стандартных прикладных программ при постановке и решении задач линейного программирования. Использование симплекс-метода для задач линейного программирования в таблицах Excel.
-
Краткие теоретические сведения
Суть симплексного метода состоит в следующем: необходимо максимизировать (соответственно минимизировать) некий критерий при наложенных линейных ограничениях. Этим критерием может выступать валовой доход от реализации продукции, совокупные операционные расходы на производство товаров и так далее.
При этом на переменные, влияющие на значение критерия, накладываются линейные ограничения в виде уравнений или неравенств. По существу, симплекс-метод – это усовершенствованный графический метод решения задач ЛП в многомерном пространстве.
Подобно тому, как графический метод ищет оптимум в вершинах многоугольника, в симплексном методе оптимум ищется в вершинах n-мерного многогранника, называемого симплексом (см. на рисунке условное изображение симплекса; красным показан путь из опорной точки к точке оптимума).
Алгоритм симплекс-метода
Последовательность действий можно описать следующим образом:
-
путем преобразований система ограничений приводится к необходимой, так называемой базисной, форме; -
находится так называемое опорное решение, служащее «точкой отсчета»; -
последовательно перебираются вершины симплекса. Если в данной точке значение критерия больше (или меньше) предыдущего, то процесс продолжается. Когда значение критерия уже нельзя улучшить, значит, решение найдено.
То есть, смысл симплексного метода следующий: все линейные неравенства, которым в многомерном пространстве соответствуют полуплоскости, ограничивают некий симплекс. При этом уравнению, описывающему оптимизируемый критерий, соответствует гиперплоскость.
Теперь нужно просто найти ту вершину симплекса, одновременно принадлежащую этой гиперплоскости, координаты которой максимизируют (минимизируют) критерий. Следовательно, выбирается базисная вершина и по ней мы
передвигаемся от одной вершины к другой, пока не найдем точку оптимума.
Практический пример применения симплексного метода
Решим симплексным методом задачу. Максимизируем функцию
L=X+Z→max
при ограничениях
{Y−X+Z=1,X−2Z+T=2.
У нас есть четыре переменные – X,Y,Z,T – причем критерий зависит лишь от двух переменных. Примем Т и Y за базисные переменные и выразим их через остальные две свободные переменные. Получим:
L=X+Z→max,
{Y=1+X−Z,T=2−X+2Z.
При X и Z равных нулю, базисные переменные равны Y=1,T=2. Значение критерия L=0. Значит, точка (1,0,0,2) является базисным решением. Начнем перебор вершин симплекса. Увеличить критерий можно увеличив Z до единицы. Тогда при Z=1,X=0 базисные переменные примут значения Y=0,T=4. Новое допустимое решение – это точка (0,0,1,4), критерий равен L=1.
Теперь выразим Z и T через Y и X:
L=1−Y+2X→max,
{Z=1−Y+Z,T=4−2Y+X.
Увеличить L можно только увеличив X. Однако X можно увеличивать бесконечно, исходня из системы уравнений. Следовательно, критерий L будет принимать неограниченно большие значения, решения задачи симплекс-методом не существует. В этом случае говорят, что имеет случай бесконечного симплекса.
-
Задание
Для того чтобы решить задачу ЛП в табличном процессоре Microsoft Excel, необходимо выполнить следующие действия:
1. Ввести условие задачи:
a) создать экранную форму для ввода условия задачи:
-
переменных, -
целевой функции (ЦФ), -
ограничений, -
граничных условий;
b) ввести исходные данные в экранную форму:
-
коэффициенты ЦФ, -
коэффициенты при переменных в ограничениях, -
правые части ограничений;
c) ввести зависимости из математической модели в экранную форму:
-
формулу для расчета ЦФ, -
формулы для расчета значений левых частей ограничений;
d) задать ЦФ (в окне "Поиск решения"):
-
целевую ячейку, -
направление оптимизации ЦФ;
e) ввести ограничения и граничные условия (в окне "Поиск решения"):
-
ячейки со значениями переменных, -
граничные условия для допустимых значений переменных, -
соотношениямежду правыми и левыми частями ограничений.
2. Решить задачу:
a) установить параметры решения задачи (в окне "Поиск решения");
b) запустить задачу на решение (в окне "Поиск решения");
c) выбрать формат вывода решения (в окне "Результаты поиска решения").
Рассмотрим подробно использование MS Excel на примере решения следующей задачи.
Фабрика выпускает два вида каш для завтрака - "Crunchy" и "Chewy". Используемые для производства обоих продуктов ингредиенты в основном одинаковы и, как правило, не являются дефицитными. Основным ограничением, накладываемым на объем выпуска, является наличие фонда рабочего времени в каждом из трех цехов фабрики.
Управляющему производством необходимо разработать план производства на месяц. В приведенной ниже таблице указаны общий фонд рабочего времени и число человеко-часов, требуемое для производства 1 т продукта.
Таблица 1
| Цех | Необходимый фонд рабочего времени чел.-ч/т | Общий фонд рабочего времени чел.-ч. в месяц | |
| “Crunchy” | “Chewy” | ||
| А. Производство | 10 | 4 | 1000 |
| В. Добавка приправ | 3 | 2 | 360 |
| С. Упаковка | 2 | 5 | 600 |
Доход от производства 1 т "Crunchy" составляет 150 ф. ст., а от производства "Chewy" - 75 ф, ст. На настоящий момент нет никаких ограничений на возможные объемы продаж. Имеется возможность продать всю произведенную продукцию.
Требуется:
а) Сформулировать модель линейного программирования, максимизирующую общий доход фабрики за месяц.
б) Решить ее c помощью MS Excel.
Формальная постановка данной задачи имеет вид:
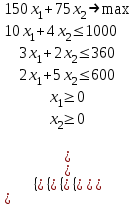
Ввод исходных данных
Создание экранной формы и ввод исходных данных
Экранная форма для решения в MS Excel представлена на рисунке 1.
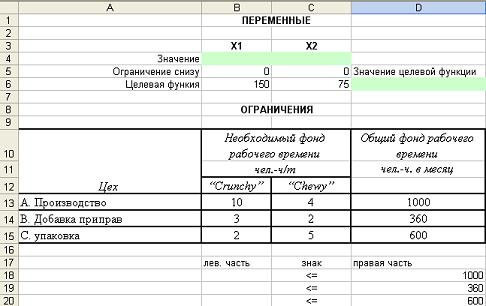
Рис.1
В экранной форме на рисунке 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка на листе Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным соответствуют ячейки B4(x1), C4 (x2), коэффициентам ЦФ соответствуют ячейки B6 (c1=150), C6 (c2=75), правым частям ограничений соответствуют ячейки D18 (b1=1000), D19 (b2=360), D20 (b3=600) и т.д.
Ввод зависимостей из формальной постановки задачи в экранную форму
Для ввода зависимостей определяющих выражение для целевой функции и ограничений используется функция MS Excel СУММПРОИЗВ, которая вычисляет сумму по парных произведений двух или более массивов.
Одним из самых простых способов определения функций в MS Excel является использование режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки "
Рис. 2
Так, например, выражение для целевой функции из задачи 1 определяется следующим образом:
-
курсор в поле D6; -
нажав кнопку " ",вызовите окно"Мастер функций – шаг 1 из 2";
",вызовите окно"Мастер функций – шаг 1 из 2"; -
выберите в окне "Категория" категорию "Математические"; -
в окне "Функция" выберитефункцию СУММПРОИЗВ (Рис. 3);
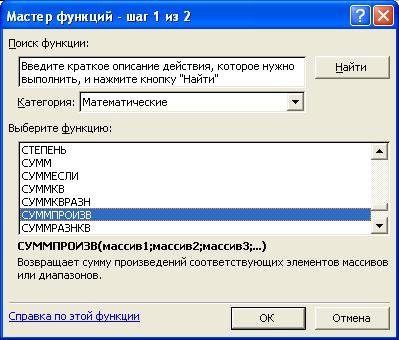
Рис. 3
-
в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$4:C$4, а в строку "Массив 2" – выражение B6:C6 (Рис. 4);
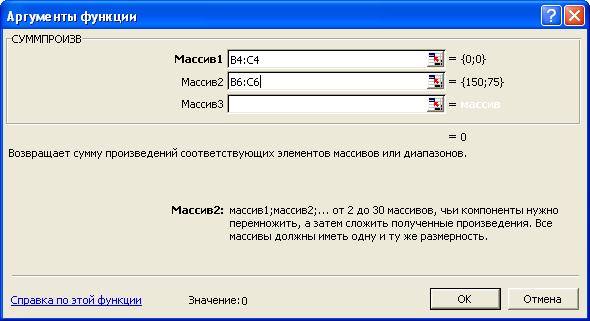
Рис. 4
Левые части ограничений задачи представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B13, C13 – 1-е ограничение; B14, С14 – 2-е ограничение и B15, С15 – 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в таблице 1.
Таблица 1.
Формулы, описывающие ограничения модели (1)
| Левая часть ограничения | Формула Excel |
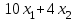 или или 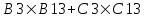 | =СУММПРОИЗВ(B4:C4;B13:C13)) |
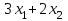 или или 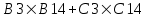 | =СУММПРОИЗВ(B4:C4;B14:C14)) |
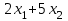 или или 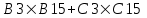 | =СУММПРОИЗВ(B4:C4;B15:C15) |
Задание ЦФ
Дальнейшие действия производятся в окне "Поиск решения", которое вызывается из меню "Сервис" (Рис.5):
-
поставьте курсор в поле "Установить целевую ячейку"; -
введите адрес целевой ячейки $D$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме ¾ это будет равносильно вводу адреса с клавиатуры; -
введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке "максимальному значению".