ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 198
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
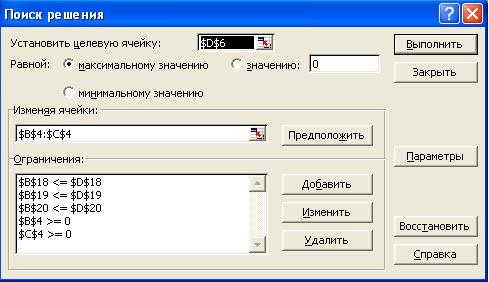
Рис. 5
Ввод ограничений и граничных условий
Задание ячеек переменных
В окно "Поиск решения" в поле "Изменяя ячейки" впишите адреса $B$4:$С$4. Необходимые адреса можно вносить в поле "Изменяя ячейки" и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
Задание граничных условий для допустимых значений переменных
В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (Рис. 1).
-
Нажмите кнопку "Добавить", после чего появится окно "Добавление ограничения" (Рис.6). -
В поле "Ссылка на ячейку" введите адреса ячеек переменных $B$4:$С$4. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме. -
В поле знака откройте список предлагаемых знаков и выберите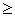 .
. -
В поле "Ограничение" введите 0.
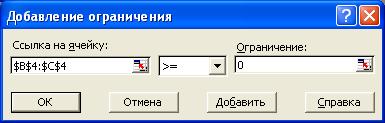
Рис.6
Задание знаков ограничений
-
Нажмите кнопку "Добавить" в окне "Добавление ограничения". -
В поле "Ссылка на ячейку" введите адрес ячейки левой части конкретного ограничения, например $B$18. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме. -
В соответствии с условием задачи выбрать в поле знака необходимый знак, например,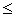 .
. -
В поле "Ограничение" введите адрес ячейки правой части рассматриваемого ограничения, например $D$18. -
Аналогично введите ограничения: $B$19<=$D$19, $B$20<=$D$20. -
Подтвердите ввод всех перечисленных выше условий нажатием кнопки OK.
Окно "Поиск решения" после ввода всех необходимых данных задачи (1) представлено на Рис. 5.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки "Изменить" или "Удалить" (см. Рис. 5).
Решение задачи
Установка параметров решения задачи
Задача запускается на решение в окне "Поиск решения". Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку "Параметры" и заполнить некоторые поля окна "Параметры поиска решения" (Рис. 7).
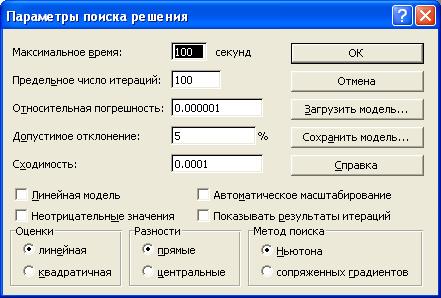
Рис. 7
Параметр "Максимальное время" служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр "Предельное число итераций" служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Параметр "Относительная погрешность" служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр "Допустимое отклонение" служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр "Сходимость" применяется только при решении нелинейных задач.Установка флажка "Линейная модель" обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.
Подтвердите установленные параметры нажатием кнопки "OK".
Запуск задачи на решение
Запуск задачи на решение производится из окна "Поиск решения" путем нажатия кнопки "Выполнить".
После запуска на решение задачи ЛП на экране появляется окно
"Результаты поиска решения" с сообщением об успешном решении задачи, представленном на Рис. 8.
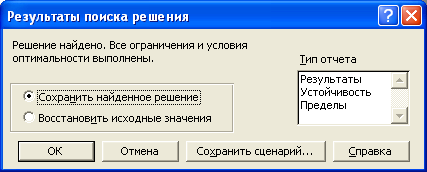
Рис. 8
Появление иного сообщения свидетельствуетт не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.
Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра "Относительная погрешность" не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.
В окне "Результаты поиска решения" представлены названия трех типов отчетов: "Результаты", "Устойчивость", "Пределы". Они необходимы при анализе полученного решения на чувствительность. Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку "OK". После этого в экранной форме появляется оптимальное решение задачи (Рис. 9).
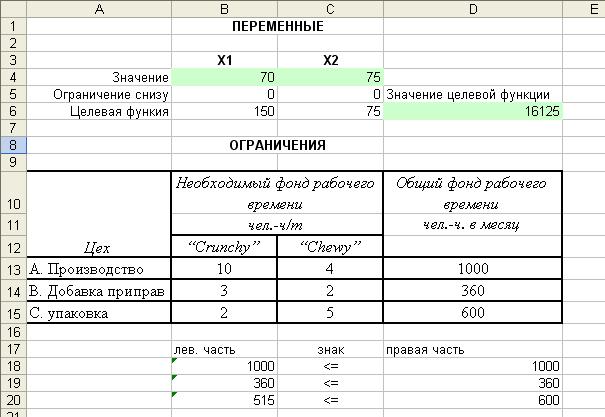
Рис.9
-
Индивидуальные задания
Варианты заданий
1. Нефтяная компания "РТ" для улучшения эксплуатационных качеств и снижения точки замораживания дизельного топлива, которое она производит, добавляет в него определенные химикаты. В каждом бензобаке объемом 1000 л должно содержаться не менее 40 мг химической добавки X, не менее 14 мг химической добавки Y и не менее 18 мг химической добавки Z. Необходимые химические добавки в форме готовых смесей поставляют "РТ" две химические компании А и В. В нижеследующей таблице приведено содержание химических добавок в каждом продукте, поставляемом указанными компаниями.
| Продукт | Химические добавки, мг/л | ||
| X | Y | Z | |
| A | 4 | 2 | 3 |
| B | 5 | 1 | 1 |
Стоимость продукта А — 1,50 ф. ст. за 1 л, а продукта В — 3,00 ф. ст. за 1 л. Требуется: найти ассортиментный набор продуктов А и В, минимизирующий общую стоимость добавленных в топливо химикатов.
2. "Princetown Paints Ltd" выпускает три основных типа румян — жидкие, перламутровые и матовые — с использованием одинаковых смесеобразующих машин и видов работ. Главному бухгалтеру фирмы было поручено разработать для компании план производства на неделю. Информация о ценах продаж и стоимости 100 л товара приведена в таблице (ф. ст.).
| | Румяна | ||
| Жидкие | Перламутровые | Матовые | |
| Цена продажи на 100 л | 120 | 126 | 110 |
| Издержки производства на 100 л: | | ||
| Стоимость сырья | 11 | 25 | 20 |
| Стоимость трудозатрат | 30 | 36 | 24 |
| Стоимость приготовления смеси | 32 | 20 | 36 |
| Другие издержки | 12 | 15 | 10 |
Стоимость 1 чел.-ч составляет 3 ф. ст. а стоимость 1 ч приготовления смеси -4 ф. ст. Фонд рабочего времени ограничен 8000 чел.-ч. в неделю, а ограничение на фонд работы смесеобразующих машин равно 5900 ч. в неделю.
В соответствии с контрактными соглашениями компания должна производить 25000 л матовых румян в неделю. Максимальный спрос на жидкие румяна равен 35000 л в неделю, а на перламутровые румяна — 29000 л в неделю.
Требуется: определить оптимальные объемы производства в неделю, при которых достигается максимальное значение получаемой за неделю прибыли, и соответствующее значение прибыли.
3. Компания "Bermuda Paint" — частная промышленная фирма, специализирующаяся на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства единицы полировочного и матового лаков.
| Лак | Цена продажи 1 галлона, ф. ст. | Издержки производства 1 галлона, ф. ст. |
| Матовый | 13,0 | 9,0 |
| Полировочный | 16,0 | 10,0 |
Для производства 1 галлона матового лака необходимо затратить 6 мин трудозатрат, а для производства одного галлона полировочного лака — 12 мин. Резерв фонда рабочего времени составляет 400 чел.-ч. в день. Размер ежедневного запаса необходимой химической смеси равен 100 унциям, тогда как ее расход на один галлон матового и полировочного лаков составляет 0,05 и 0,02 унции соответственно. Технологические возможности завода позволяют выпускать не более 3000 галлонов лака в день.
В соответствии с соглашением с основным оптовым покупателем компания должна поставлять ему 5000 галлонов матового лака и 2500 галлонов полировочного лака за каждую рабочую неделю (состоящую из 5 дней). Кроме того, существует профсоюзное соглашение, в котором оговаривается минимальный объем производства в день, равный 2000 галлонов. Администрации данной компании необходимо определить ежедневные объемы производства каждого вида лаков, которые позволяют получать максимальный общий доход.
Требуется: определить ежедневный оптимальный план производства и соответствующую ему величину дохода.
4. Три завода поставляют некоторую разновидность стали на пять торговых складов. Спрос каждого торгового склада в декабре, наличие стали на заводах, а также значения стоимости транспортировки 1 т стали приведены в нижеследующей таблице.
| Завод | Транспортные издержки, ф. ст. за единицу Торговый склад | Предложение т | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| A | 20 | 27 | 33 | 25 | 34 | 200 |
| B | 22 | 36 | 34 | 28 | 26 | 250 |
| C | 26 | 29 | 27 | 26 | 28 | 300 |
| Потребность, т | 100 | 150 | 200 | 100 | 200 | |