Добавлен: 06.11.2023
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1-6.
Решить задачу, используя классическую формулу определения вероятности. Зенитноракетный комплекс состоит из 22 орудий, 7 из них современного образца. На позицию случайным образом отобраны 3 орудия. Найти вероятность того, что 2 орудия из них будут современного образца?
Согласно классическому определению вероятность этого события равна:
,где
- число исходов, благоприятствующих событию А, а 
- общее число исходов. В данном случае исходом будет отбор трех орудий. Согласно правил комбинаторики: 
Благоприятный исход – это отбор двух орудий современного образца и одного обычного:
Вероятность отбора 2 орудий современного образца из трех:
Задача 2-6.
Решить задачу, используя теоремы сложения и умножения вероятностей. Чемпион мира по шахматам проводит сеанс одновременной игры. Среди участников игры 2 гроссмейстера. Вероятность победы чемпиона над первым гроссмейстером равна 0,7 , над вторым – 0,75. Какова вероятность, что чемпион потерпит 2 поражения?
Поражение одному гроссмейстеру не зависит от поражения другому, значит эти события независимы. Следовательно вероятность двух поражений будет равна определению двух вероятностей. Вероятность поражения первому гроссмейстеру равна 0,3, второму 0,25. Вероятность поражения обоим:
Задача 3-6.
Решить задачу, используя формулу Бернулли.
Вероятность того, что отобранная для проверки деталь будет стандартной
, равна 0,8.Какова вероятность того, что из 7 взятых деталей 3 будут стандартными?
Формула Бернулли:
В данном случае событие А(выбранная деталь стандартна) должно произойти в
случаях из 
с вероятностью 
, а вероятность того что деталь окажется нестандартной 
.
Задача 4-6.
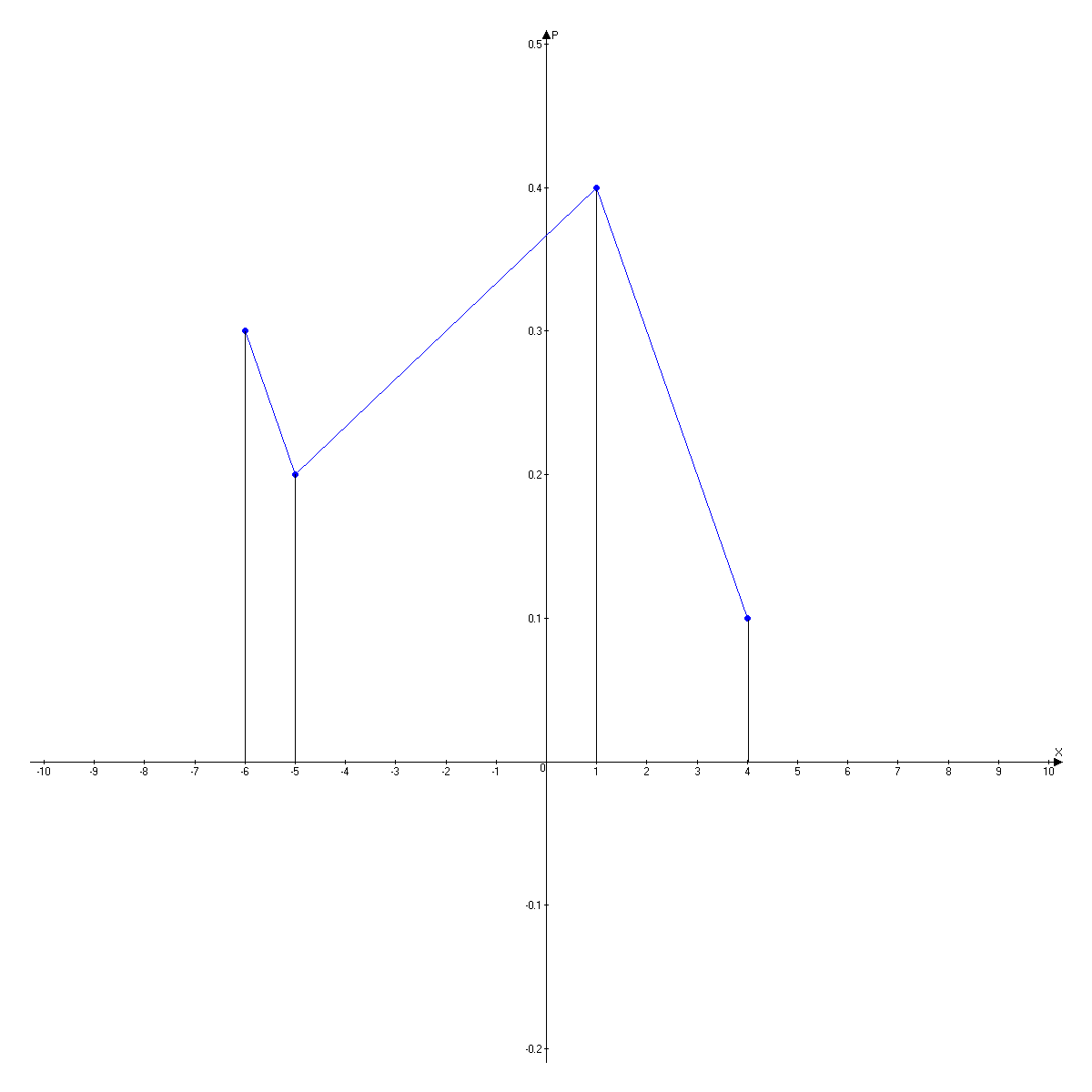
Дан ряд распределения дискретной случайной величины.
Построить многоугольник распределения, найти математическое ожидание, дисперсию и среднеквадратическое отклонение.
| X | -6 | -5 | 1 | 4 |
| P | 0,3 | 0,2 | 0,4 | 0,1 |
Многоугольгик распределения:
Математическое ожидание находим по формуле
:
Дисперсию находим по формуле
:
Среднеквадратическое отклонение:
