Файл: Тема 6. Математические основы реляционных баз данных.pdf
Добавлен: 20.10.2018
Просмотров: 860
Скачиваний: 8

Тема 6. Математические основы реляционных баз данных
Языки запросов позволяют задавать операции над РБД и указывать
предикаты для искомых данных.
Языки запросов делятся на два класса:
Алгебраические языки, выражающие запросы в терминах операций
над отношениями;
Языки исчисления предикатов, в которых запрос является
описанием искомых записей, задаваемым в форме предиката.
Рассмотрим реляционную алгебру. Будем предполагать, что доступ к
компонентам кортежей возможен как по номерам компонентов, так и по
именам атрибутов. Порядок компонентов предполагается существенным, все
отношения конечны. Операндами реляционной алгебры являются постоянные
или переменные отношения фиксированной арности.
Основные операции
1. Объединение
Объединение отношений R и S (обозначается R S) есть множество
кортежей, которые принадлежат либо R, либо S, либо им обоим. Арность R и S
одинакова. В символической форме объединение записывается так:
R S = { t | t R t S}.
2. Разность
Разностью отношений R и S (обозначается R-S) называется множество
кортежей, принадлежащих R, но не принадлежащих S. Арность R и S
одинакова. Символически: R-S = { t | t R & t S}.
3. Декартово произведение
Пусть R и S – отношения арности r и s соответственно. Тогда декартовым
произведением R S отношений R и S называется множество кортежей длины
r+s, первые r компонентов которых образуют кортежи из R, а последние s
компонентов - кортежи из S.
R S = {(a
1
,a
2
,…a
r
,
ar+1
,
ar+2
…a
r+s
) | (a
1
,a
2
,…a
r
) R & (a
r+1
,a
r+2
…a
r+s
) S}.
4. Проекция

Пусть R - отношение арности r. Проекцией R на компоненты i
1
,i
2
,…i
m
называется множество кортежей вида (a
1
,a
2
,…a
m
) таких, что существует кортеж
(b
1
,b
2
,…b
r
) R, удовлетворяющий условию a
j
= b
ij
(j=1 .. m). Проекция
обозначается
)
(
2
1
R
m
i
i
i
.
))}
,
1
(
(
)
,
,
(
|
)
,
,
{(
)
(
2
1
2
1
2
1
m
j
b
a
R
b
b
b
a
a
a
R
j
m
i
j
r
m
i
i
i
Существо этой операции состоит в том, что из каждого кортежа
отношения R формируется новый кортеж, состоящий из перечисленных
компонентов в указанном порядке. Например, для построения
)
(
1
,
2
R
нужно из
каждого кортежа t R сформировать кортеж t , состоящий из второго и первого
компонентов кортежа t в указанном порядке.
Если отношение имеет именованные столбцы (атрибуты), то вместо
номеров компонентов можно использовать имена атрибутов. Например, для
отношения R со схемой R(A,B,C,D) проекция
)
(
,
R
A
B
есть то же самое, что и
)
(
1
,
2
R
.
5. Селекция
Пусть F - формула, операндами которой являются константы или номера
компонентов, а операциями – сравнения и логические операции «&», « », « ».
Селекция отношения R по формуле F (обозначается
)
(R
F
) есть множество
кортежей t таких, что при подстановке i–го компонента t вместо каждого
вхождения номера i в формулу F для всех i она станет истинной. Например,
)
(
3
2
R
обозначает множество кортежей из R, второй компонент которых
больше третьего. Селекция
)
(
1
1
R
Вася
Петя
есть множество кортежей из R, первый
компонент которых имеет значение Петя или Вася. Формулы могут ссылаться
на компоненты по именам атрибутов:
)}
(
&
|
{
)
(
t
F
R
t
t
R
F
Примеры:

Дополнительные алгебраические операции
1. Пересечение.
R S = R- (R-S).
2. Частное.
Пусть R и S отношения арности r и s соответственно, r>s и S 0. Тогда
частное R и S (записывается R S) есть множество кортежей длины r-s таких,
что для всех кортежей u S кортеж tu принадлежит R.
3. Соединение.
-соединение R и S по столбцам i и j (записывается
S
R
j
i
), где -
операция сравнения, есть краткая запись для
)
(
)
(
S
R
j
r
i
(r – арность R). –
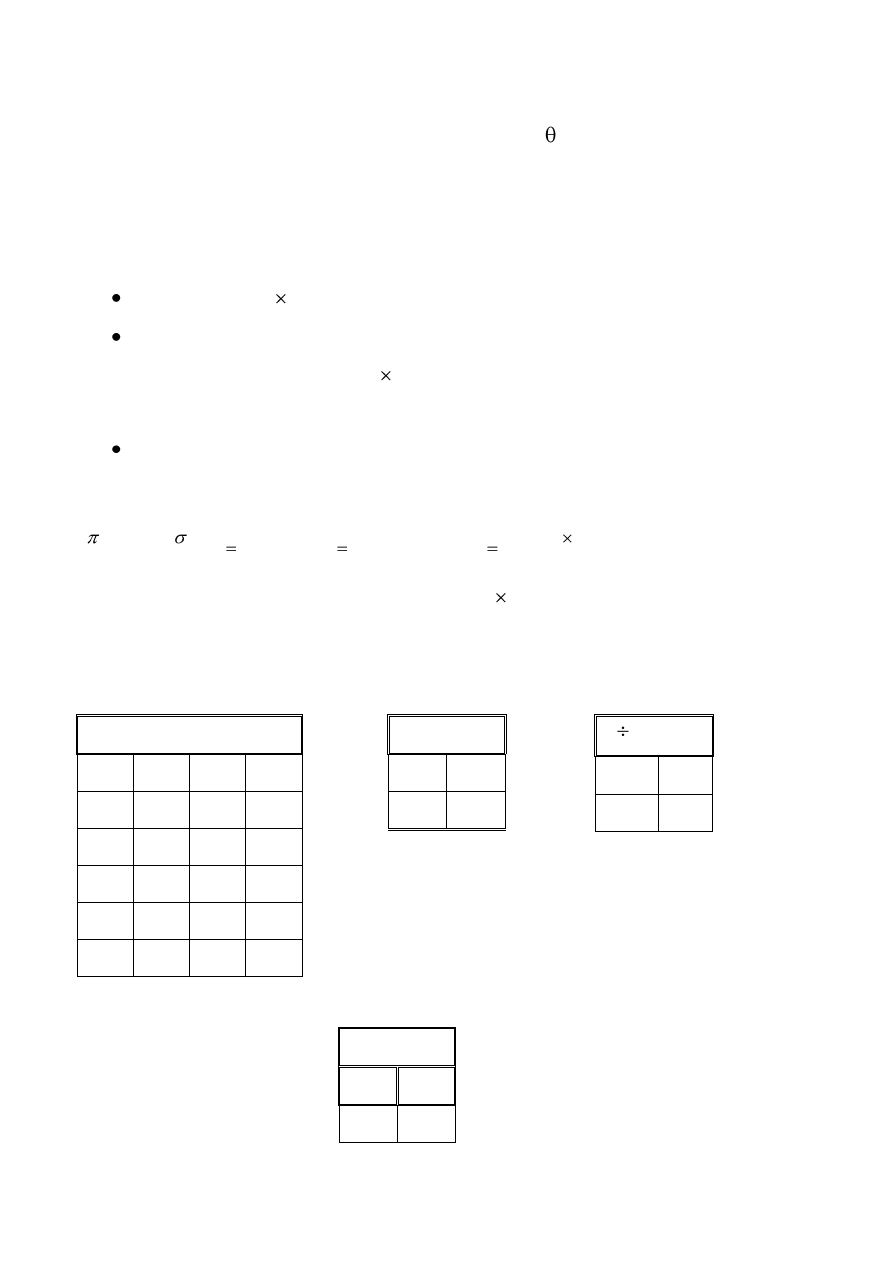
R
A
B
C
a
b
C
d
a
F
c
b
D
S
D
E
F
b
G
a
d
A
f
R S
a
b
c
d
a
f
c
b
d
R-S
a
b
C
c
b
D
B=b
(R)
A
B
C
a
b
c
c
b
d
R S
A
B
C
D
E
F
a
B
c
b
g
A
a
B
c
d
a
F
d
A
f
b
g
A
d
A
f
d
a
F
…
…
…
…
…
…
A,C
(R)
A
C
a
c
d
f
c
d
соединение R и S есть множество таких кортежей в декартовом произведении R
и S, что i–ый компонент R находится в отношении с j–ым компонентом S.
4. Естественное соединение.
Естественное соединение R и S обозначается
S
R
, требует
именованных атрибутов. Вычисляется следующим образом:
Вычисляется R S;
Для каждого атрибута A, имеющегося и в отношении R и в отношении S,
выбираются те кортежи R S, у которых совпадают значения в столбцах
R.A и S.A;
Для каждого указанного A удаляется S.A.
Формально, если A
1
,A
2
,…A
k
имеются и в R и в S, то
S
R
есть
))
(
.
.
&
...
&
2
,
1
2
.
&
.
1
.
(
2
1
S
R
k
A
S
k
A
R
A
S
A
R
A
S
A
R
m
i
i
i
,
где
m
i
i
i
2
1
-
упорядоченный список всех компонентов R S, за исключением компонентов
S.A
1
,…S.A
k
.
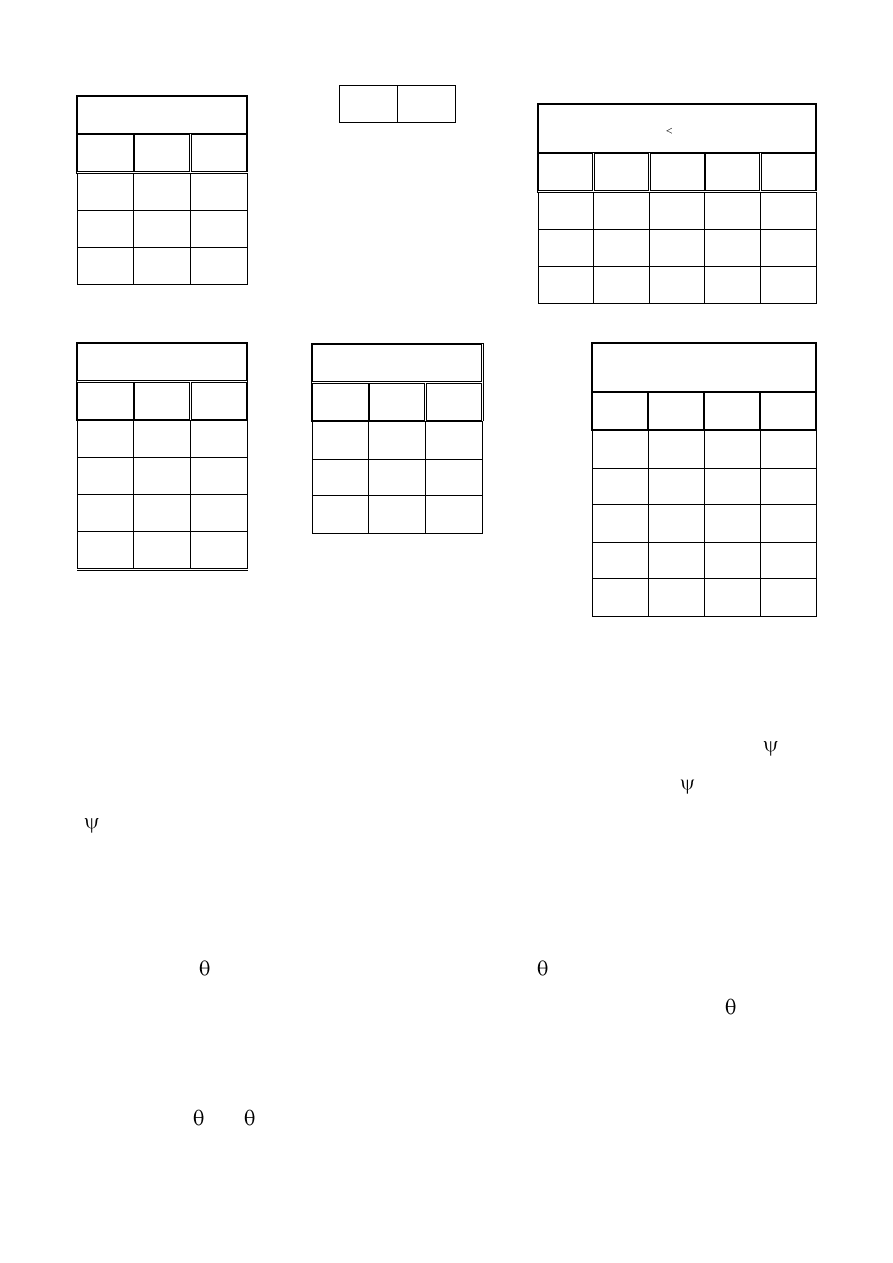
Примеры:
R
a
b
C
d
a
b
E
f
b
c
E
f
e
d
C
d
e
d
E
f
a
b
D
e
S
c
d
e
f
R S
a
b
e
d
S
D
E
3
1
Реляционное исчисление
Исчисление с переменными-кортежами
Выражение реляционного исчисления с переменными-кортежами {t| (t)}
представляет множество кортежей t, удовлетворяющих условию (t). Формула
строится из атомов и операций.
Атомы:
1. R(s), где R - отношение, s - переменная-кортеж. Атом утверждает, что
s - кортеж отношения R.
2. s[i] u[j], где s,u - переменные кортежи, - операция сравнения. Атом
утверждает, что i–ый компонент s находится в отношении с j–ым
компонентом u. Например, s[1]<u[3] означает, что 1-ый компонент s
меньше 3-го компонента u.
3. s[i] a и a s[i], где a – константа.
Формулы:
6
2
S
R
D
B
A
B
C
D
E
1
2
3
3
1
1
2
3
6
2
4
5
6
6
2
R
A
B
C
1
2
3
4
5
6
7
8
9
R
A
B
C
a
b
C
d
b
C
b
b
F
c
a
D
S
B
C
D
b
c
d
b
c
e
a
d
b
S
R
A
B
C
D
a
b
c
d
a
b
c
e
d
b
c
d
d
b
c
e
c
a
d
b