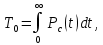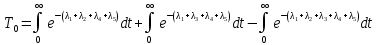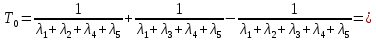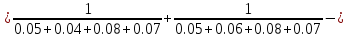Файл: На испытании находилось N.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 07.11.2023

Просмотров: 228

Скачиваний: 8

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задание №1

На испытании находилось No неремонтируемых элементов БРЭО. Число отказов n(∆t) фиксировалось через каждые 100 ч работы (∆t = 100 ч). Данные об отказах приведены в таблице 1. Требуется вычислить количественные характеристики надежности и построить зависимости характеристик от времени.

Таблица 1 – Данные об отказах


∆ti, ч
N(∆ti)
∆ti, ч
N(∆ti)

Вариант №12

0 - 100
79
1500 - 1600
48

100 - 200
71
1600 - 1700
47

200 - 300
66
1700 - 1800
42

300 - 400
65
1800 - 1900
36

400 -500
64
1900 - 2000
34

500 -600
61
2000 - 2100
34

600 - 700
64
2100 - 2200
25

700 - 800
62
2200 - 2300
24

800 -900
61
2300 - 2400
19

900 - 1000
60
2400 - 2500
17

1000 - 1100
59
2500 - 2600
14

1100 -1200
57
2600 - 2700
23

1200 - 1300
57
2700 - 2800
24

1300 - 1400
56
2800 - 2900
25

1400 - 1500
50
2900 - 3000
10



1) Вероятность безотказной работы



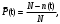
где
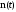
– число отказавших изделий к настоящему времени;







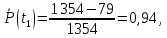
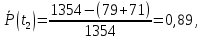
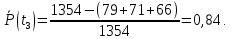
Аналогичным образом вычисляются вероятности безотказной работы значения для всех остальных интервалов, результаты приведены в таблице ниже.
2) Частота отказов

Статистическая оценка частоты отказов, 1/ч,



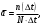
где 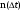– число отказавших изделий в интервале времени;

– интервал времени, для которого определяется частота отказов;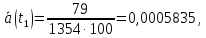







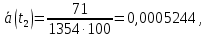
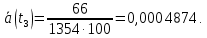
Аналогичным образом вычисляется частота отказов для всех остальных интервалов, результаты приведены в таблице ниже.
3) Интенсивность отказов

Среднее число исправно работающих объектов в каждом интервале



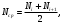
где Ni – число объектов, исправно работающих в начале интервала;

Ni+1 – число объектов, исправно работающих в конце интервала;



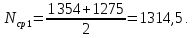
Аналогичным образом вычисляется среднее число работающих элементов для всех остальных интервалов, результаты приведены в таблице ниже.

Статическая оценка интенсивности отказов, 1/час,









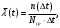
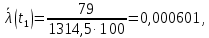
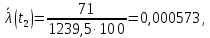
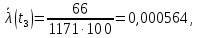
Аналогичным образом вычисляется интенсивность отказов для всех остальных интервалов, результаты приведены в таблице ниже.

Таблица 2 – Результаты расчетов

t
n(t)
N
P(t)
∆t
a(t)
Ni
Ni+1
Nср
λ(t)

0-100
79
1354
0,94
100
0,0005835
1354
1275
1314,5
0,000601

100-200
71
1354
0,89
100
0,0005244
1275
1204
1239,5
0,000573

200-300
66
1354
0,84
100
0,0004874
1204
1138
1171
0,000564

300-400
65
1354
0,79
100
0,0004801
1138
1073
1105,5
0,000588

400-500
64
1354
0,75
100
0,0004727
1073
1009
1041
0,000615

500-600
61
1354
0,70
100
0,0004505
1009
948
978,5
0,000623

600-700
64
1354
0,65
100
0,0004727
948
884
916
0,000699

700-800
62
1354
0,61
100
0,0004579
884
822
853
0,000727

800-900
61
1354
0,56
100
0,0004505
822
761
791,5
0,000771

900-1000
60
1354
0,52
100
0,0004431
761
701
731
0,000821

1000-1100
59
1354
0,47
100
0,0004357
701
642
671,5
0,000879

1100-1200
57
1354
0,43
100
0,000421
642
585
613,5
0,000929

1200-1300
57
1354
0,39
100
0,000421
585
528
556,5
0,001024

1300-1400
56
1354
0,35
100
0,0004136
528
472
500
0,00112

1400-1500
50
1354
0,31
100
0,0003693
472
422
447
0,001119

1500-1600
48
1354
0,28
100
0,0003545
422
374
398
0,001206

1600-1700
47
1354
0,24
100
0,0003471
374
327
350,5
0,001341

1700-1800
42
1354
0,21
100
0,0003102
327
285
306
0,001373

1800-1900
36
1354
0,18
100
0,0002659
285
249
267
0,001348

1900-2000
34
1354
0,16
100
0,00025
249
215
232
0,001466

2000-2100
34
1354
0,13
100
0,00025
215
181
198
0,001717

2100-2200
25
1354
0,12
100
0,00018
181
156
168,5
0,001484

2200-2300
24
1354
0,10
100
0,00018
156
132
144
0,001667

2300-2400
19
1354
0,08
100
0,00014
132
113
122,5
0,001551

2400-2500
17
1354
0,07
100
0,00013
113
96
104,5
0,001627

2500-2600
14
1354
0,06
100
0,00010
96
82
89
0,001573

2600-2700
23
1354
0,04
100
0,00017
82
59
70,5
0,003262

2700-2800
24
1354
0,03
100
0,00018
59
35
47
0,005106

2800-2900
25
1354
0,01
100
0,00018
35
10
22,5
0,011111

2900-3000
10
1354
0,00
100
0,00007
10
0
5
0,02



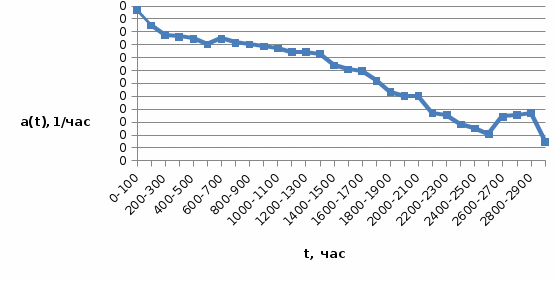
Рисунок 1



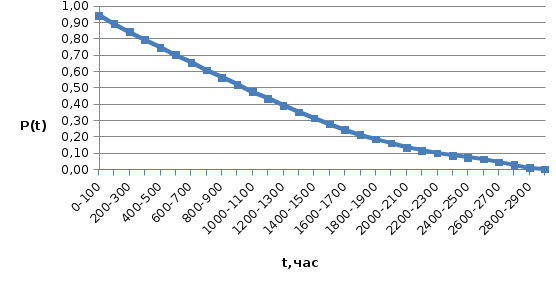
Рисунок 2



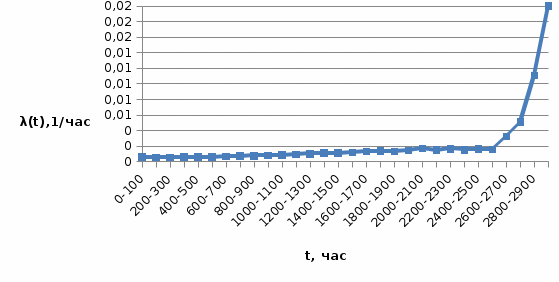
Рисунок 3

4) Средняя наработка до первого отказа, час,






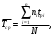
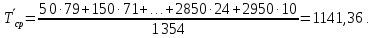
Задание №2

Составить уравнение надежности, оценить величины вероятности безотказной работы ????????(????) и наработки на отказ ????отк(????) для заданного варианта структурной схемы при длительности рабочего цикла t=3 час Интенсивность отказов элементов приведена в таблице 3.

Таблица 3 – Интенсивность отказов элементов

№ элемента
????????(????), ч−????

1
0,05

2
0,04

3
0,06

4
0,08

5
0,07




Рисунок 4 – Вариант структурной схемы.
Решение. Формулы для средней наработки до первого отказа в данном случае нет. Поэтому следует воспользоваться выражением



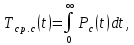
Найдем вероятность безотказной работы Рc(t) устройства:









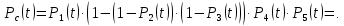
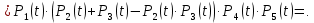
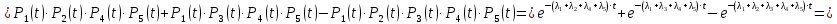
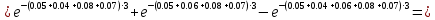
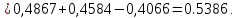
Средняя наработка до отказа,час,







Смотрите также файлы