Лабораторная работа №1

Работа с векторами и матрицами

Задание 1

Решение:

>> a=[12 43 7 14 85 3]

>> b = [12;43;7;14;85;3]

>> M = [13,45,6;34,16,97;0,27,3;44,5,74]



Рисунок 1

Задание 2

Решение:

>> x=0:3:0.2

>> y=cos(x)



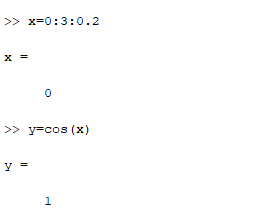
Рисунок 2

Задание 3

Решение:

>> c1= linspace(1,30)



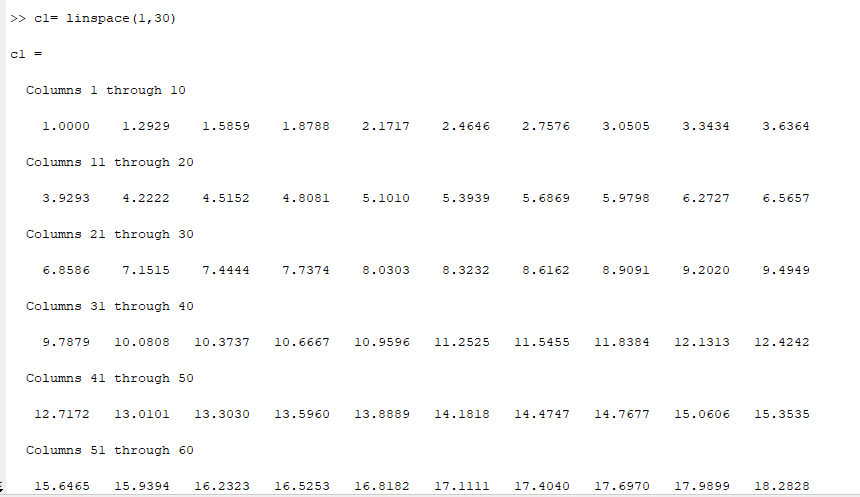
Рисунок 3

Задание 4

Решение:

>> clear

>> a = [1 2 3 4; 5 6 7 8; 9 10 11 12; 13 14 15 16]

>> a(2,3)=13

>> a(4,:)=0

>> a(:,2)=25



Рисунок 4



Рисунок 5

Задание 5

Решение:

>> clear a

>> A = [0 0 0 0; 2 2 2 2; 4 4 4 4; 6 6 6 6]

>> A(:,3)=[]

>> A(2,:)=[]

>> A(1,1:end)=1



Рисунок 6

Задание 6

Решение:

>> B=ones(5,3)

>> B=zeros(5,3)

>> M4=magic(4)



Рисунок 7

Лабораторная работа №2

Матричные операции

Задание:

 Создайте две матрицы Р1 и Р2 из произвольных значений, размерами 3х4 и 4х3.

 Умножьте их друг на друга.

 Получившуюся матрицу возведите в третью степень.

 Результат транспонируйте.

 Очистите переменные P1 и Р2.

 Заполните их так как показано на картинке.

Повторите с матрицей Р1 пример 6, а с матрицей Р2 пример 7. Опишите результат.

 Объедините по вертикали получившиеся для матрицы Р1 результаты в одну матрицу двумя способами.

 Объедините по горизонтали получившиеся для матрицы Р2 результаты в одну матрицу двумя способами.

Решение:

С матрицей P1 транспонирование и умножение завершилось успешно, но с матрицей P1 деление и возведение в степень завершилось предупреждением – «Warning: Matrix is singular to working precision», что говорит о том, что матрица числа матрицы,

---

возведенные в степень, слишком большие для деления.

>> P1 = [1,1,1,1; 1,1,1,1; 1,1,1,1]

>> P2=[2,2,2;2,2,2;2,2,2;2,2,2]

>> P3=P1*P2

>> P4=P3^3

>> P5=P4.'

>> clear P1

>> clear P2

>> P1 = [1,2;5,4]

>> P2=[11,21,31;32,42,52;53,63,73]

>> K1=P1*P1'

>> K2=(P1*P1)'

>> K3=P2/P2^2

>> K4=P2^2

>> K5=P2/K4

>> [K1; K2]

>> cat(1,K1,K2)

>> K8=(P2/P2)^2

>> [K3 K8]

>> cat(2,K3,K8)











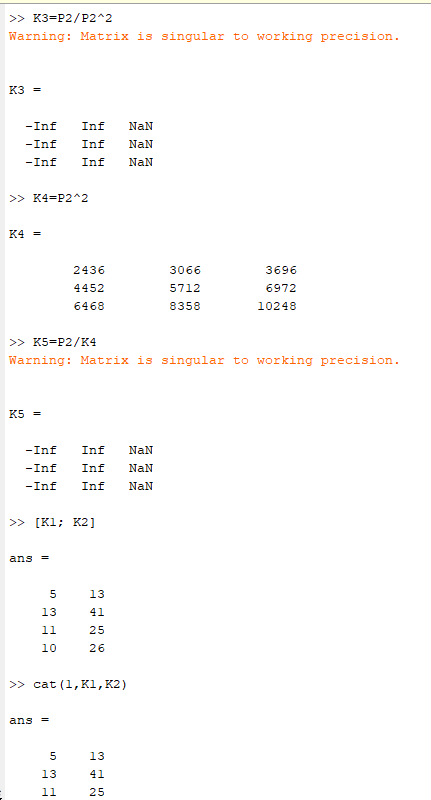
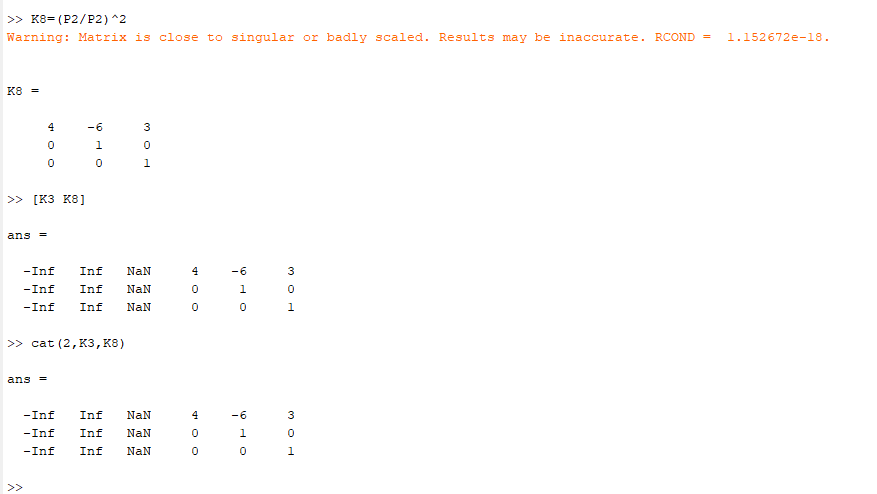
Рисунок 8-12 – Выполнение задания

Лабораторная работа №3

Построение графиков функций

Задание:

 Постройте график функции y = exp(-x)*sin(10*x). Задайте тип и цвет линии. Добавьте заголовок.

 Постройте графики функций в одних осях. y1 = exp(-x).*sin(10*x) y2 = sin(10*x) Добавьте легенду. Попробуйте перенести легенду с помощью мыши в другое место окна figure. Задайте параметр расположения легенды вне графика – в правом верхнем углу графического окна.

 Постройте графики функций: y1 = sin(x) y2 = cos(x) Подпишите оси. Добавьте сетку.

 Постройте графики функций в одном графическом окне, один под другим. y1 = sin(x) y2 = cos(x)

 Постройте четыре графика функций, каждый в своем окне, в одном figure y1=cos(x) y2=sin(x) y3=x^(1/2) y4=x^2

 Постройте график функции y = sin(x). Добавьте подписи координатных осей, сетку, команду задания границ для осей. Добавьте подпись '← sin(x)' в точке (3.05,0.16).

 Для функции n! постройте график функции в логарифмическом масштабе по оси y.

 Постройте графики функций f = log(0.5*x) g = sin(log(x)) в логарифмическом масштабе по оси х. Добавьте легенду на графики.

 Постройте графики функции y=exp(x) в обычном и логарифмическом масштабе в одном figure, но в разных осях (используйте subplot). Добавьте легенду на графики.

 Постройте график функции в полярных координатах: x=[0:0.01:2*pi] f =8*sin(x) r = cos(2*x)

---

 Постройте в полярных координатах следующие кривые: окружность, спираль Архимеда, сердце, бабочка, полярная роза.

 Постройте графики функций, заданных параметрически. Диапазон изменения параметра подберите таким образом, чтобы построенные графики были похожи на графики, приведенные на рисунках ниже. Установите толщину линии графиков в 2 пикселя. Добавьте заголовок и легенду. Сохраните построенные графики в различных графических форматах - png, jpg, eps. Сравните качество и размер получившихся графических файлов. Сделайте вывод о том, какой графический формат предпочтительнее для графиков и почему.

 Постройте график функции x*sin(1/x).

 Задайте три вектора. Первый вектор содержит номера дней месяца. Второй и третий список содержат значения курса акций в эти дни, для двух разных месяцев. Построить графики зависимости курса акций от номера дня.

 Постройте график функции sin(x). С помощью панели инструментов окна figure измените толщину линии графика, добавьте текстовую надпись. Выполните экспорт графика в файл png.

 Постройте график функции sin(x)/x. С помощью функции gtext добавьте текстовую надпись. Добавить заголовок, подписи осей, сетку и легенду, цвета для линий графиков.

Решение:

>> clear all

>> x=[0:0.005:5];

>> y = exp(-x).*sin(10*x);

>> plot(x,y,'r:')

>> x = [0:0.005:5];

>> y1 = exp(-x).*sin(10*x);

>> y2 = sin(10*x);

>> plot(x, y1,'k-',x,y2, 'k:')

>> legend('y1=exp(-x)*sin(10*x)',4)

>> xlabel('x')

>> ylabel('y')

>> x = [0:0.005:5];

y1 = sin(x);

plot(x, y1);

grid on

>> x = [0:0.005:5];

y2=cos(x);

plot(x,y2);

grid on

>> clear x

x = [0:0.005:5];

y1 = sin(x);

y2=cos(x);

plot(x, y1,x,y2);

grid on

>> x = [0:0.005:5];

y1=cos(x);

y2=sin(x);

y3=x.^(1/2);

y4=x.^2;

figure;

plot(x,y1);

figure;

plot(x,y2);

figure;

plot(x,y3);

figure;

plot(x,y4);

x = [0:0.005:5];

y=sin(x);

plot(x,y);

grid on;

text(3.05,0.16, '← sin(x)')

Y1=[1,2,3]

y=[1e+1,1e+4,1e+1,1e+3,1e+1,1e+4,1e+1];

p=semilogy(Y1),

set(p,'LineWidth',2);

title('Логарифмическая шкала по оси y')

x = [0:0.005:5];

f=log(0.5*x);

g=sin(log(x));

p = semilogx(f)

set(p, 'LineWidth',2);

t = semilogx(g)

set(t, 'LineWidth',2);

grid on

x1=[0:0.005:5];

y1=exp(x1);

x2=[0:0.005:5];

y2=exp(x2);

subplot(2,2,1)

---

P=semilogx(y2)

legend('exp')

subplot(2,2,2)

plot(x2,y2)

legend('exp')

x=[0:0.01:2*pi]

f =8*sin(x)

r = cos(2*x)

polar(x,f)

polar(x,r)

>> clear all

>> n=100;

t=0:0.01:6*pi;

r=t./(t+n);

T=[t t];

R=[r -r];

polar(T,R)

>> clear all

>> n=100;

t=0:0.01:6*pi;

r=t./(t+n);

T=[t t];

R=[r -r];

polar(T,R)

>> clear all

>> th = linspace(0,2*pi,50);

r = 10;

polar(th,r+zeros(size(th)))

>> clear all

>> t = -pi:0.1:pi;

r = ((sin(t).*sqrt(abs(cos(t))))./(sin(t) + (7/5))) - 2*sin(t) + 2 ;

polar(t,r)

>> clear all

>> theta = [0:pi/32:8*pi];

r = exp(sin(theta)) - 2*cos(4*theta) - (sin((2*theta - pi)/24)).^5;

polar(theta,r,'--r')

title('butterfly curve')

xlabel('theta (\theta)')

ylabel('r')

>> theta = [0:pi/32:8*pi];

r = exp(sin(theta)) - 2*cos(4*theta) - (sin((2*theta - pi)/24)).^5;

polar(theta,r,'--r')

xlabel('theta (\theta)')

ylabel('r')

>> clear all

>> theta = 2*pi*rand(1,50);

rose(theta)

>>

>> x = [-1/pi:0.01:1/pi];

y = x.*(sin(1./x));

plot(x,y)

>>

>> D=30;

days=1:D;

kurs1=50 + (60-50) * rand(D,1);

kurs2=60 + (70-50) * rand(D,1);

plot([kurs1,kurs2])

legend('$$$','Euro')

>> x = [0:0.005;5];

>> y=sin(x);

>> plot(x,y)

x = [-10:0.5:10]
y = sin(x)./(x);
plot(x,y);
gtext('My Plot');
legend('sin(x)/x');
grid on

---

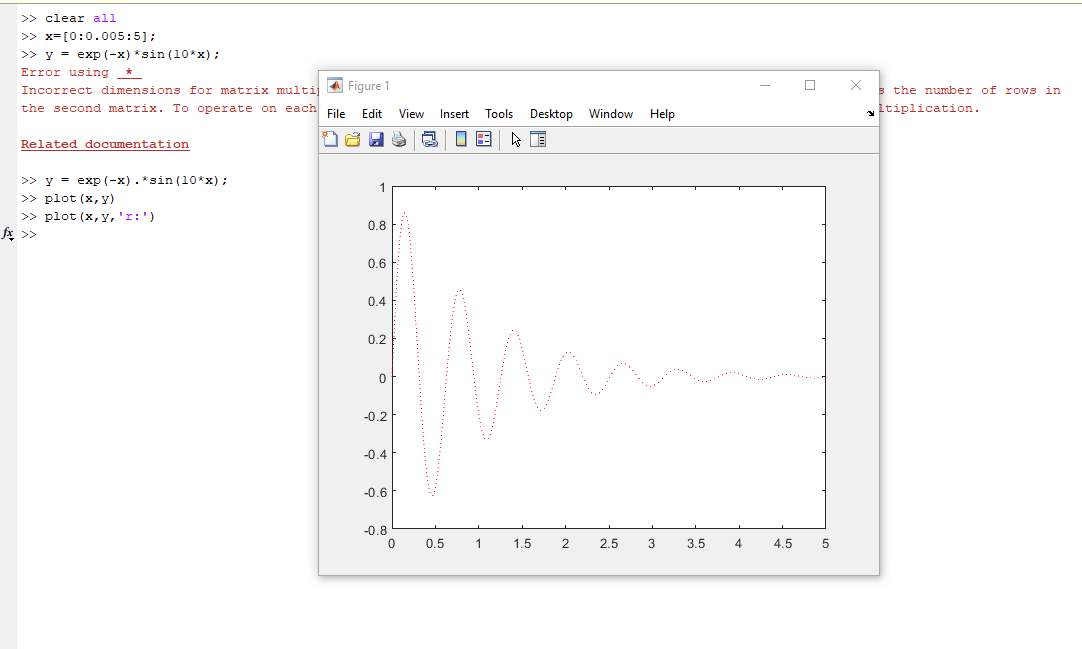
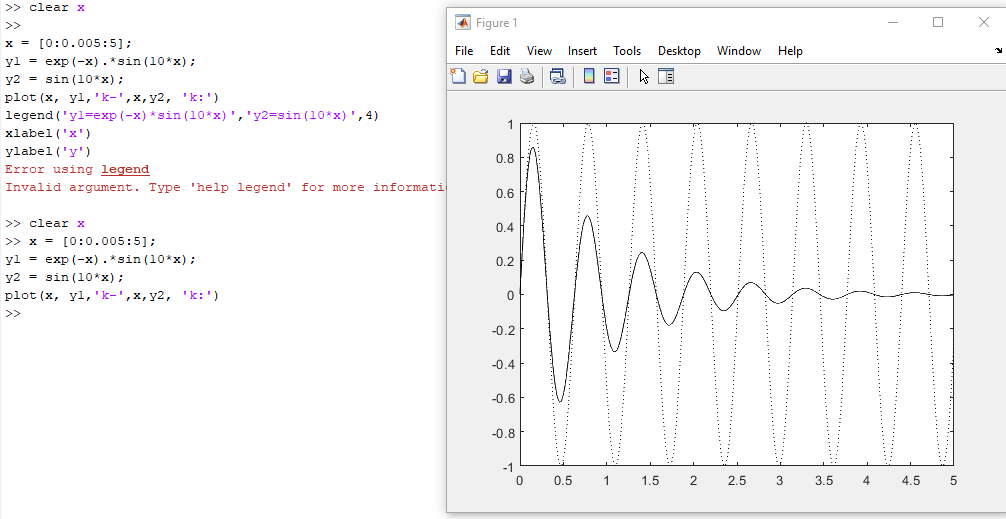
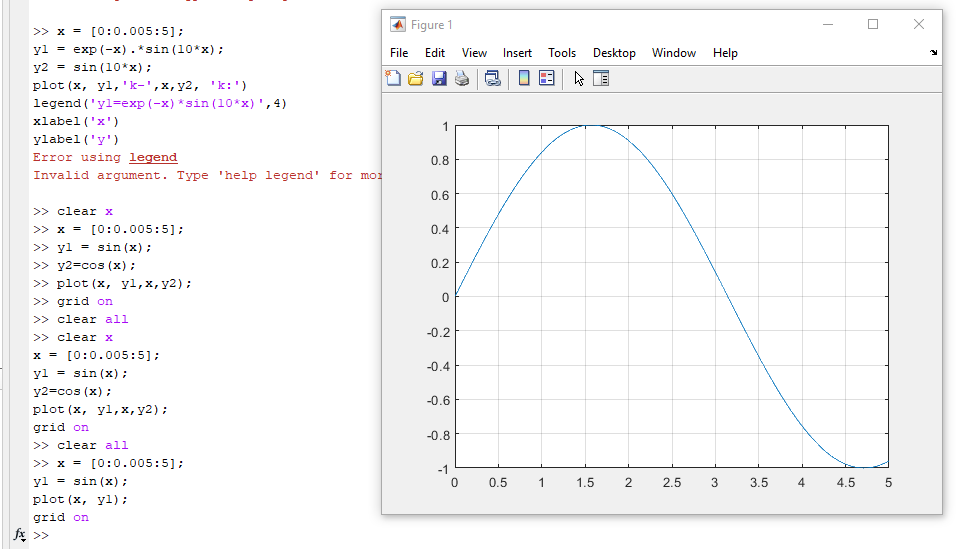
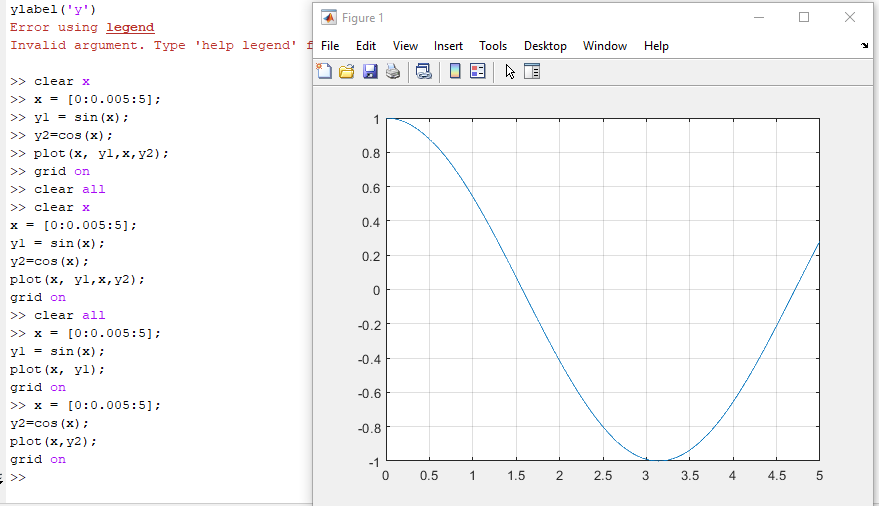
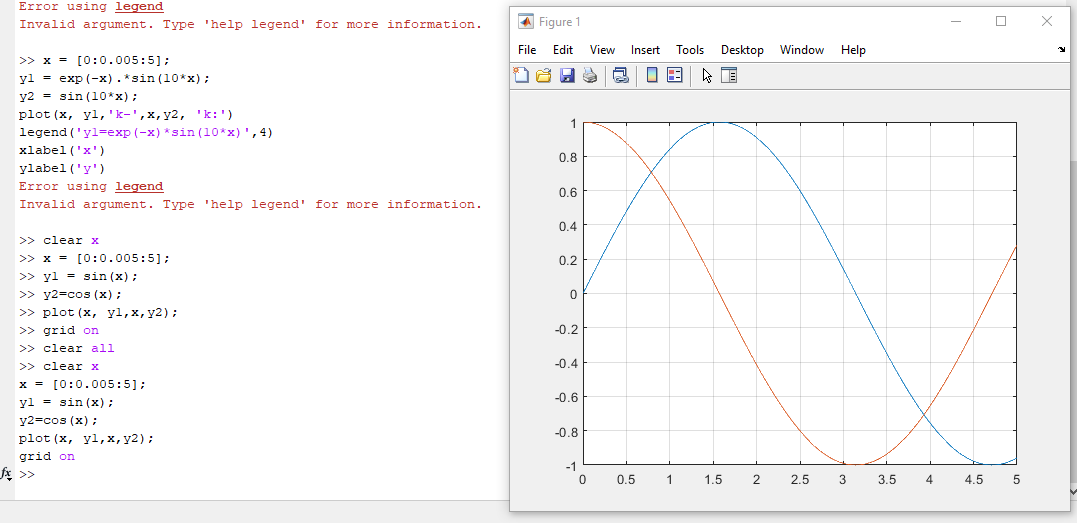
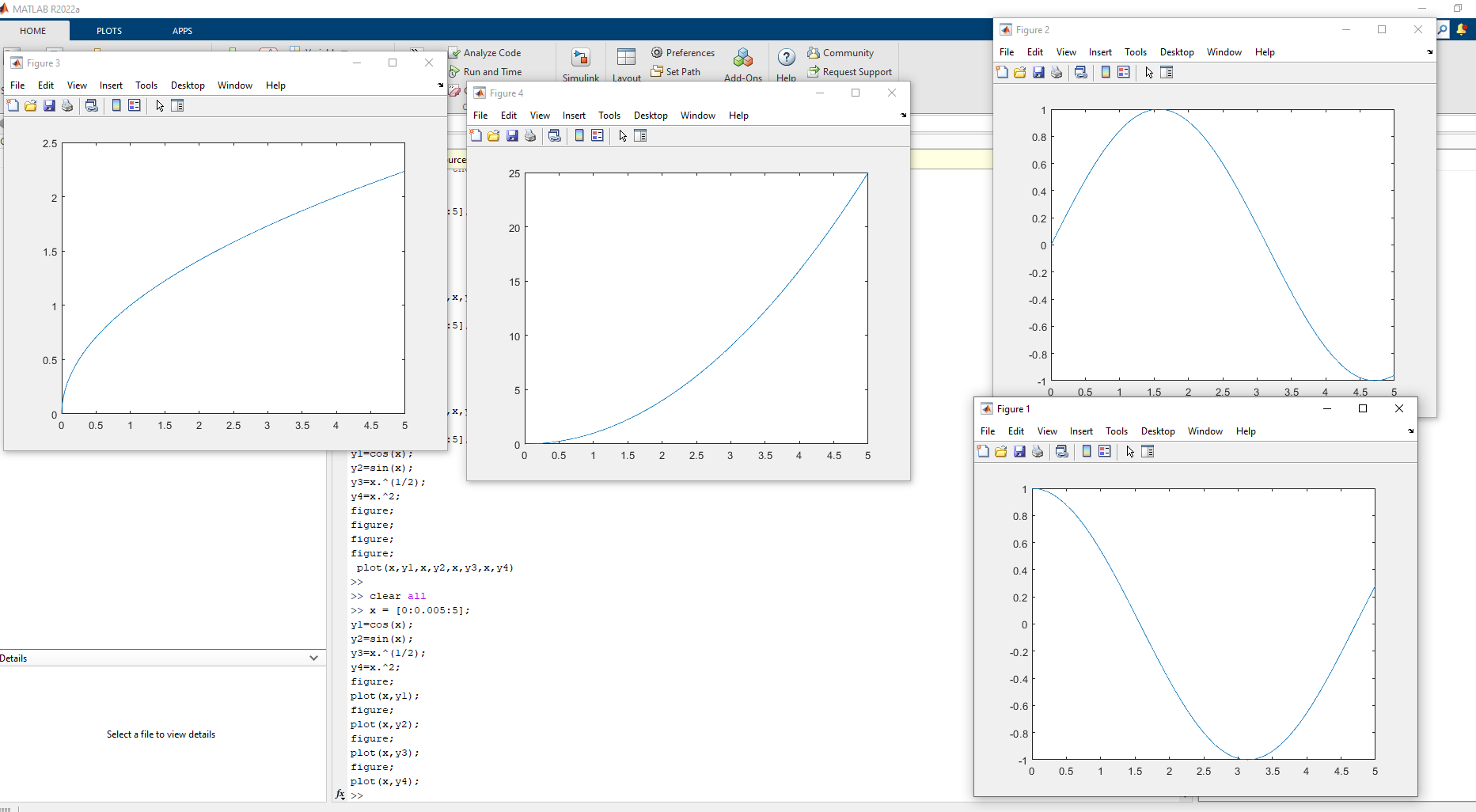
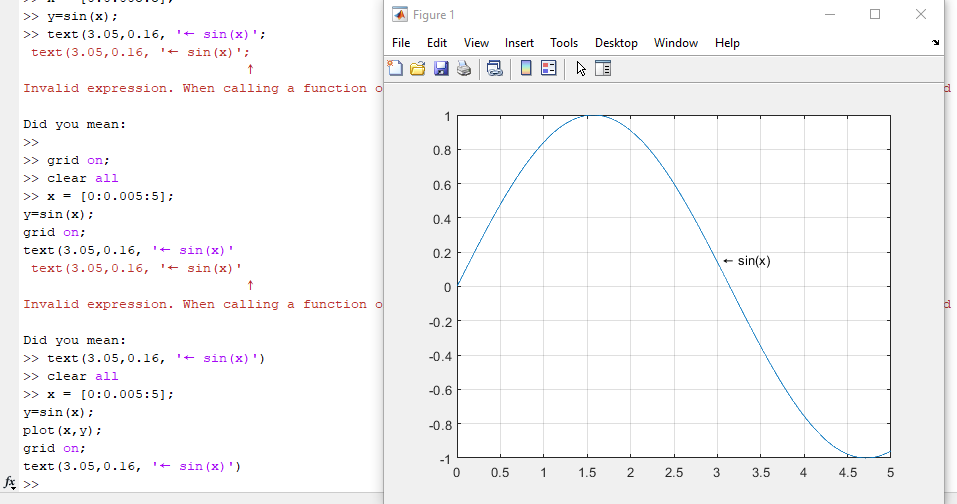
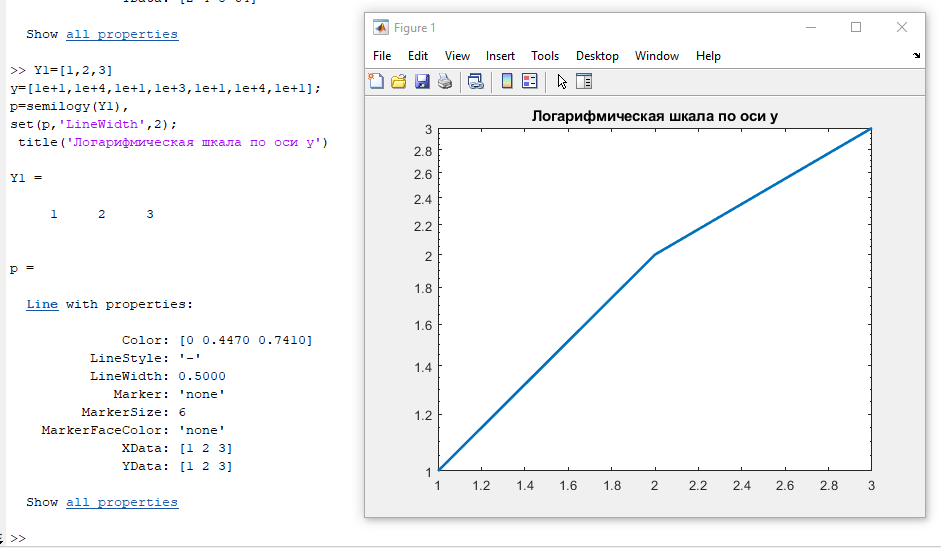
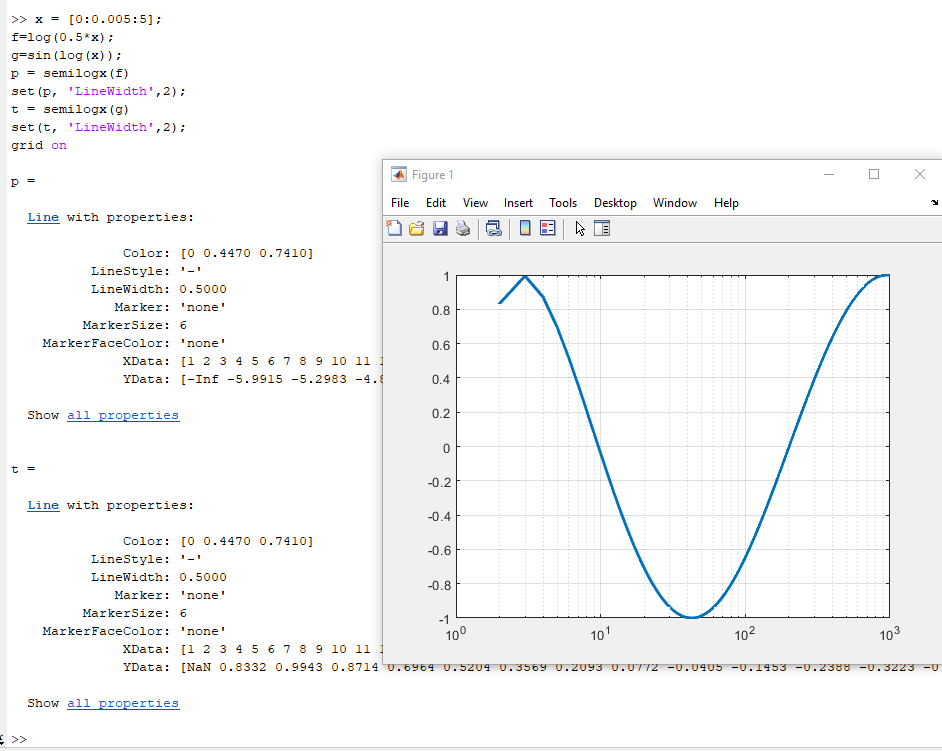
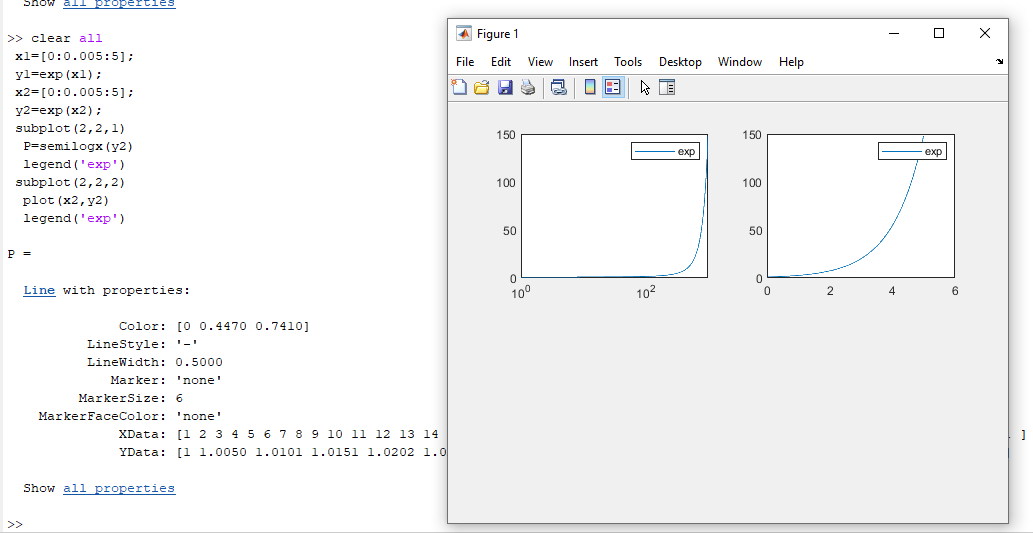
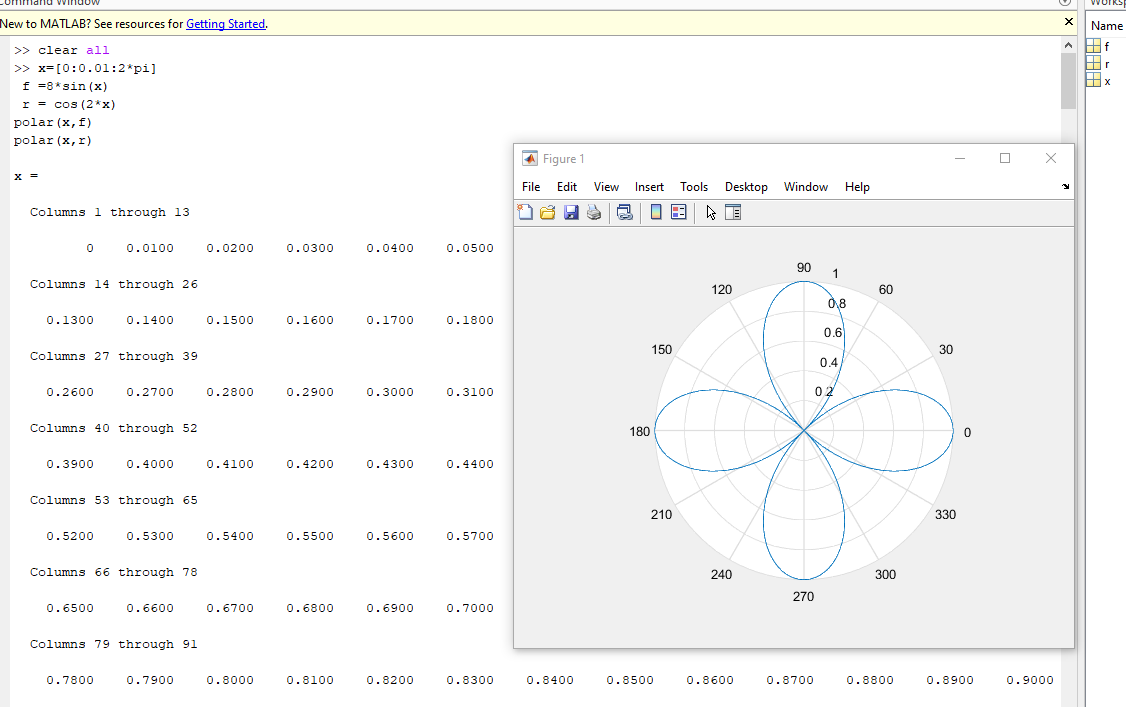
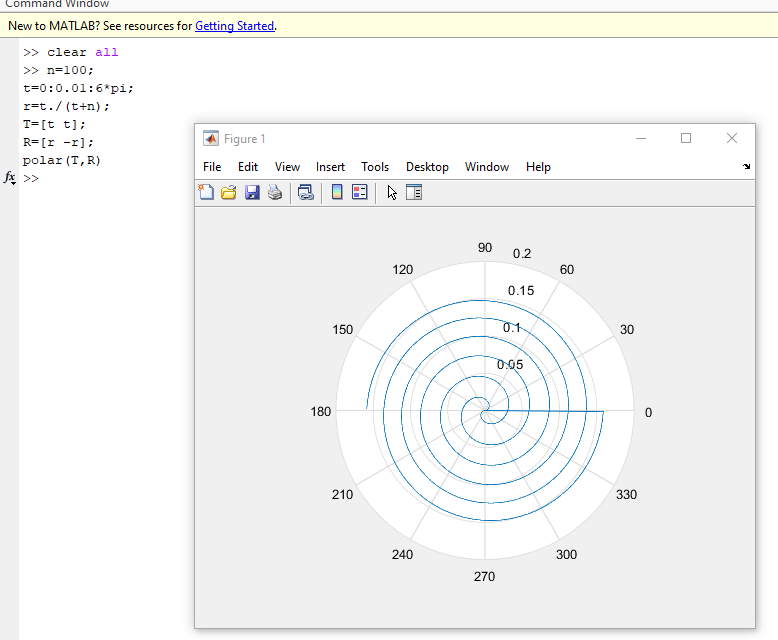
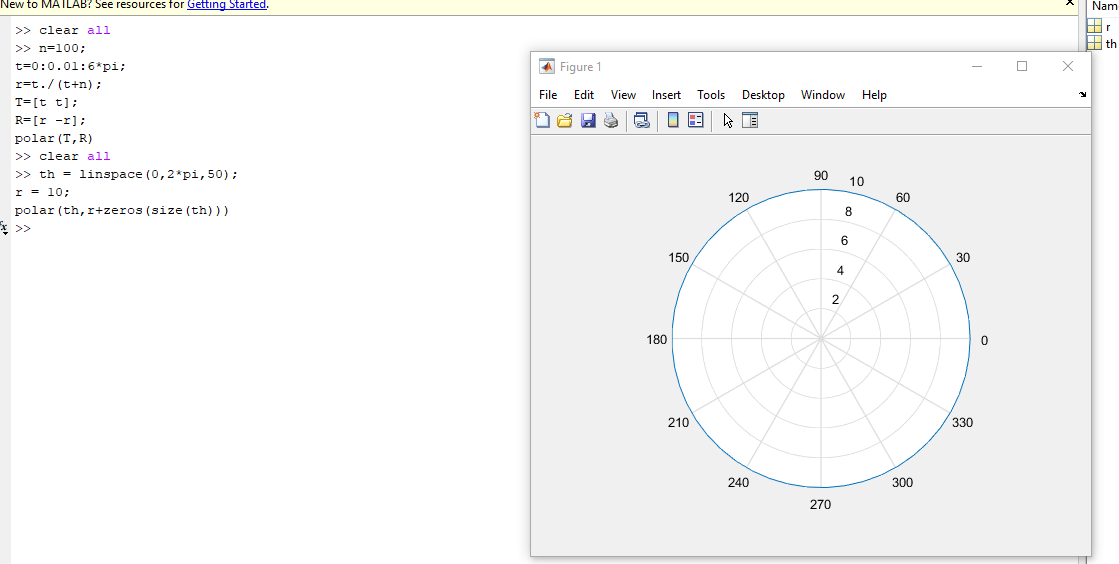
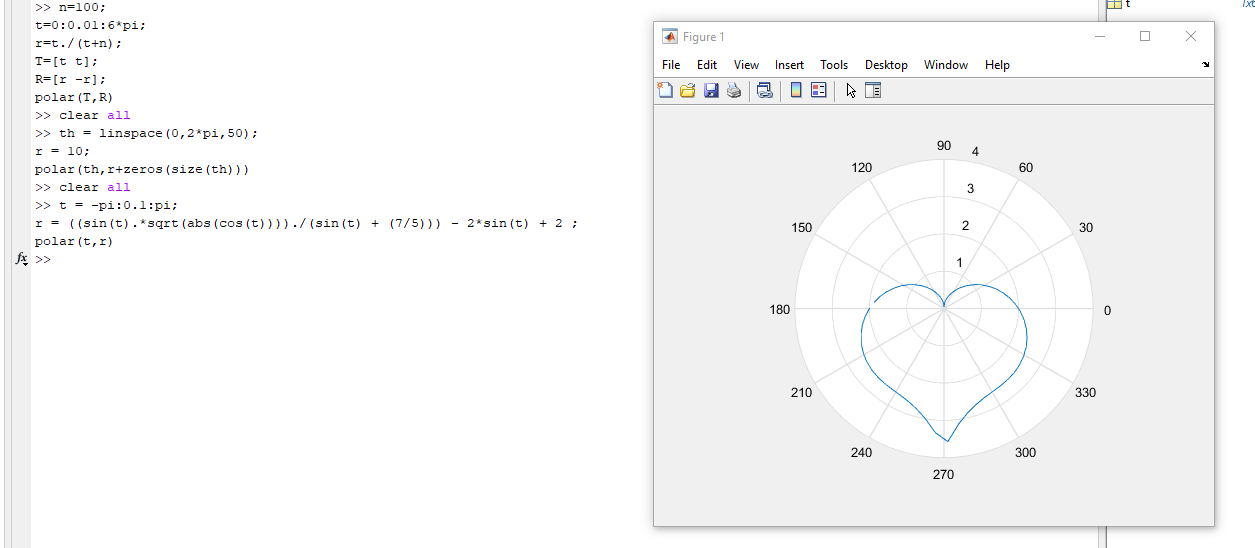
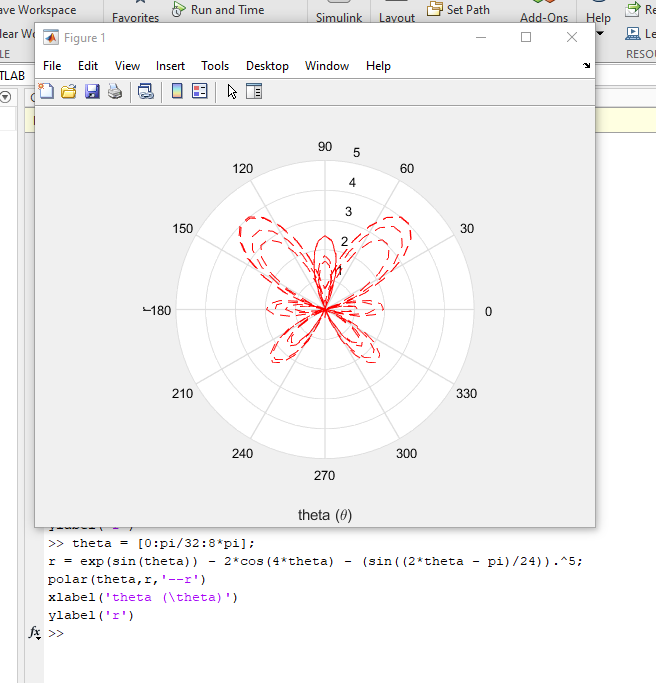
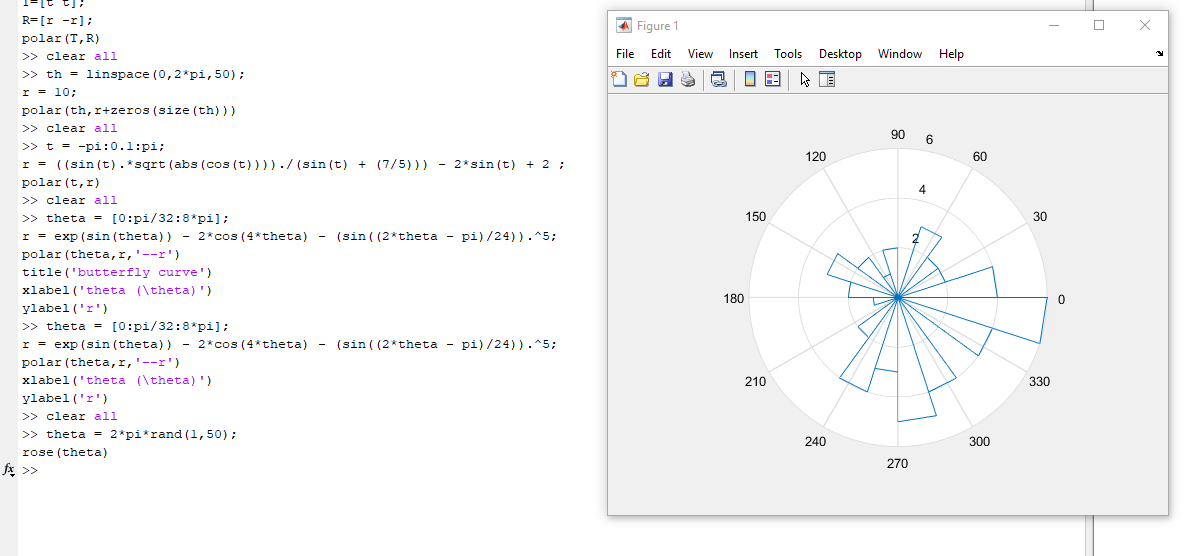
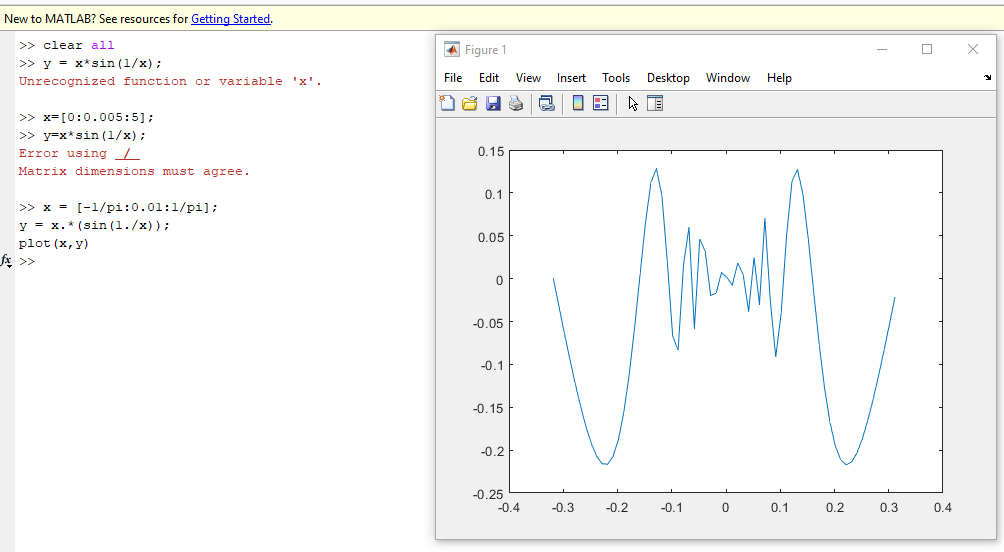
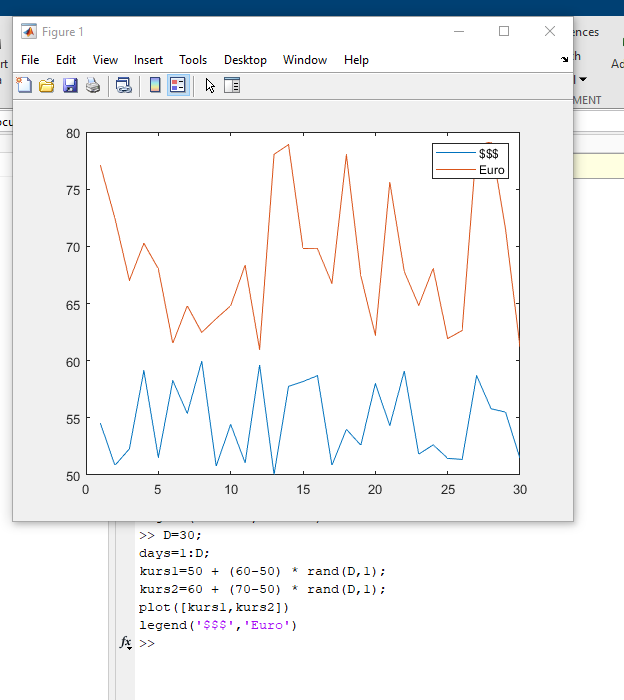
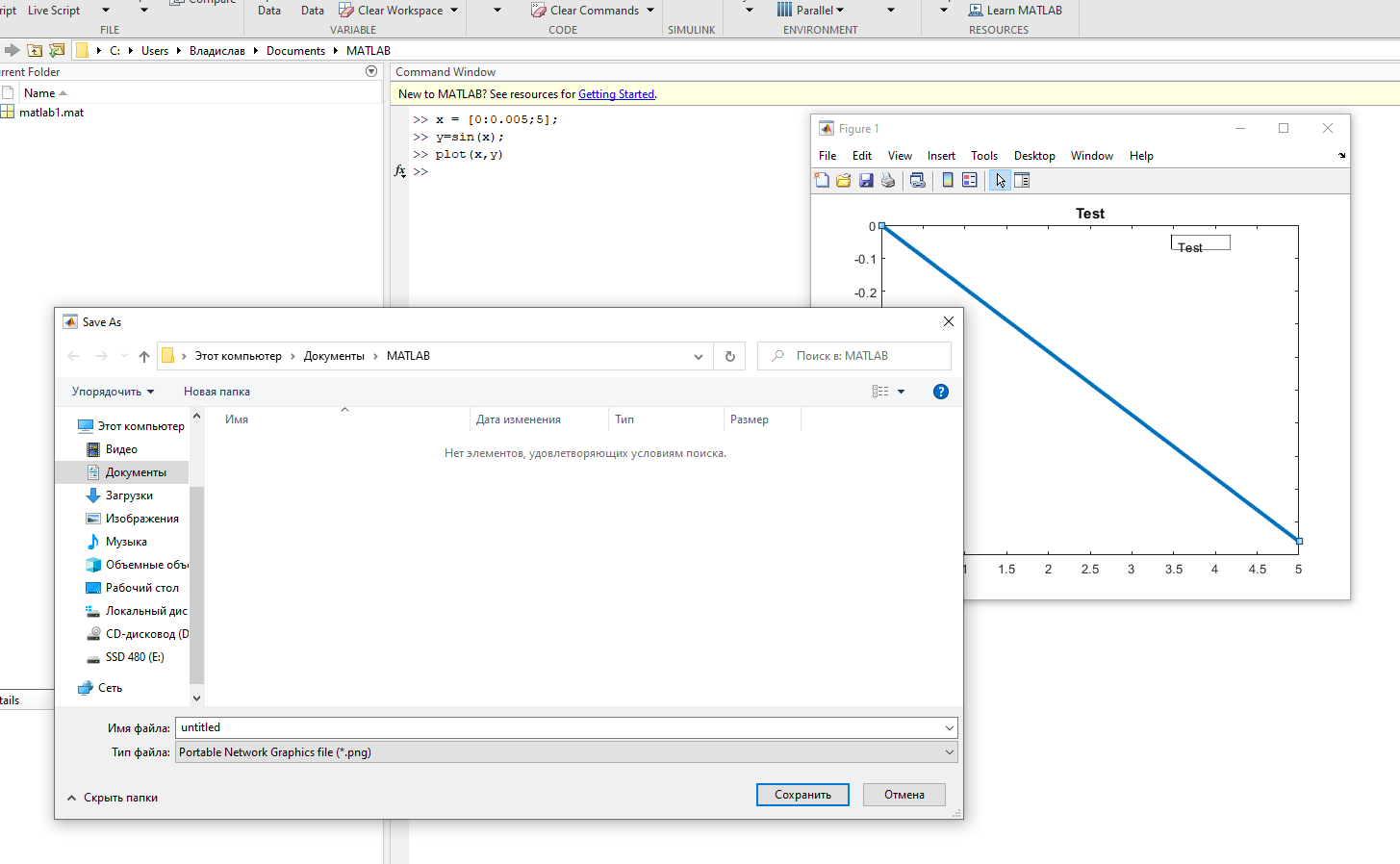
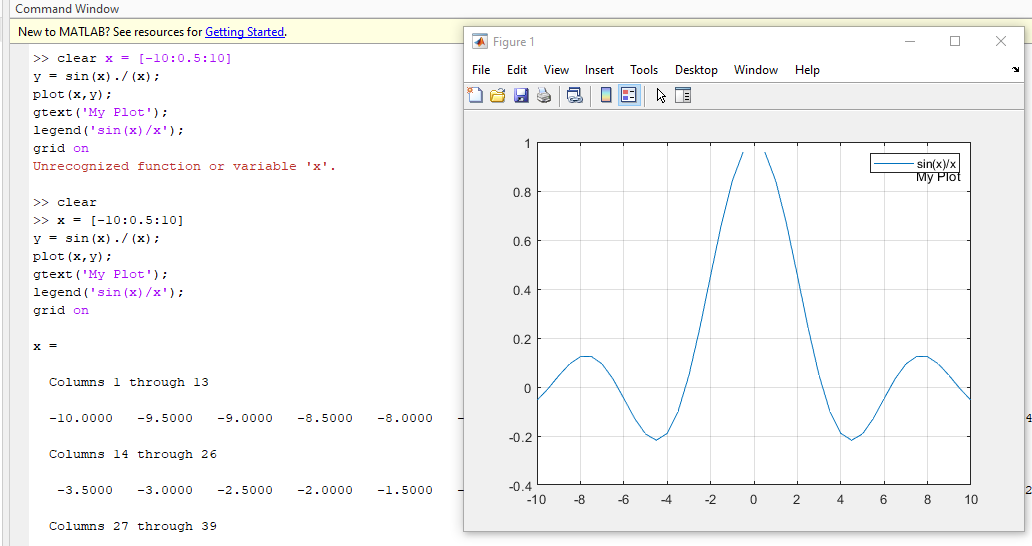
Рисунок 12-20

---

Смотрите также файлы

• Основы проектирования железных дорог.pdf

• 8. Суицидальное поведение. Другие формы аутоагрессии проституция и депрессии.docx

• Формы устройства детей, оставшихся без попечения родителей.docx

• Физикотехнологические основы получения композиционных материалов.doc

• Эпизоотолотические данные по сибирской язве.docx