Министерство образования и молодежной политик Свердловской области

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СВЕРДЛОВСКОЙ ОБЛАСТИ «ЕКАТЕРИНБУРГСКИЙ ТЕХНИКУМ АВТОМАТИКА»

ПЦК Информационно-коммуникационных технологий

КУРСОВОЙ ПРОЕКТ

по ПМ.01 Проектирование цифровых устройств

Проектирование цифрового устройства с временным разделением сигналов

Пояснительная записка

ГАПОУ СО «ЕТА» 09.02.01.2122. 16 ПЗ

Руководитель:

_____________ Лунегов О.Б.

«___»______________2022 г.

Выполнил: студент группы КСК-319

___________Подрязский А.

«___»______________2022 г.

Екатеринбург 2022

Содержание


Введение……………………………………………………………………….…..4

1 Синтез комбинационной схемы……………………………………………..…5

2 Формирователь тактовых импульсов…………………………………..……...9

3 Синтезирование счетчика………………………………………………..……11

4 Генератор тактовых импульсов……………………………………………....13

5 Расчет потребляемой мощности………………………………………..…….16

6 Расчет быстродействия…………………………………………………..……17

7 Элементная база………………………………………………………….……18

Заключение………………………………………………………………………21

Список использованных источников…………………………………………..22

Приложения……………………………………………………………………...23

Введение

Проектирование цифровых устройств – дисциплина, изучающая способы описания и преобразования структурных элементов. Предметом данной профессиональной области является математический аппарат алгебры логики, способы задания и реализации функций алгебры логики, методы, используемые при преобразовании логических структур комбинационных систем и конечных автоматов.

Проектирование цифровых устройств – сравнительно молодая и быстроразвивающаяся отрасль науки. Её появление в 30-х годах двадцатого столетия связанно с усложнением и совершенствованием релейных систем управления, когда возникла необходимость в их математическом описании. Основы теории проектирования начали закладываться в 1938 – 1940 гг., когда учёные СССР, США, Японии доказали применимость булевой алгебры логики при анализе и синтезе контактных схем. Применение аппарата алгебры логики при решении задач проектирования цифровой техники получило существенное развитие в трудах многих учёных. Создание ЭВМ внесло большой вклад в развитие теории цифровых устройств. На сегодняшний день, зачастую, без использования ЭВМ невозможно решать те или иные практические задачи, связанные с анализом, разработкой и усовершенствованием цифровых устройств.

---

Устройства промышленной автоматики, телемеханики и связи в основном относятся к классу цифровых устройств. Увеличение производительности и надёжности этих устройств – всё это, и многое другое, обусловлено постоянным развитием автоматизированных управляющих систем, базирующихся на теории проектирования цифровых устройств.

В данной работе мы разработаем цифровое устройство с временным разделением сигналов.

В начале представим структурную схему разрабатываемого устройства



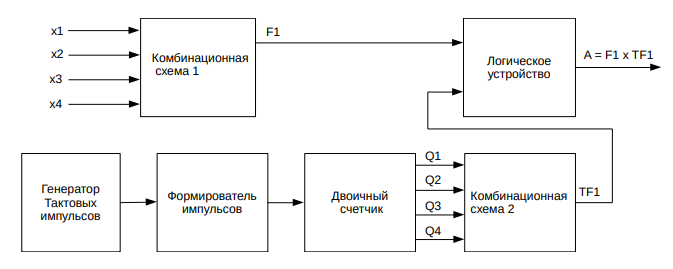
Рисунок 1 - Структурная схема разрабатываемого устройства

1 Синтез комбинационной схемы.

Основным этапом синтеза комбинационной схемы является минимизация заданных логических функций F1 с целью получения наиболее простого алгебраического выражения для каждой из них в виде минимальной дизъюнктивной нормальной формы (МДНФ) с последующей схемной реализацией минимальным числом логических элементов и, соответственно, минимальным количеством корпусов цифровых ИМС.

Составим таблицу истинности комбинационной схемы, подставим значения F, как указано в задании.

Таблица 1. Таблица истинности комбинационной схемы

№ набора	X1	X2	X3	X4	F
0	0	0	0	0	1
1	0	0	0	1	1
2	0	0	1	0	0
3	0	0	1	1	1
4	0	1	0	0	*
5	0	1	0	1	0
6	0	1	1	0	0
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	0
11	1	0	1	1	1
12	1	1	0	0	0
13	1	1	0	1	*
14	1	1	1	0	*
15	1	1	1	1	0

---

Составим совершенную нормальную дизъюнктивную форму.

Совершенная дизъюнктивная нормальная форма — одна из форм представления функции алгебры логики в виде логического выражения. Представляет собой частный случай ДНФ, удовлетворяющий следующим трём условиям:

• 
  В ней нет одинаковых слагаемых
  
• 
  В каждом слагаемом нет повторяющихся переменных
  
• 
  Каждое слагаемое содержит все переменные, от которых зависит булева функция
  

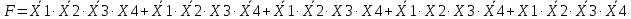(1)

При числе входных логических переменных до 5-6 наиболее эффективным методом является минимизация логических функций с использованием карт Карно.

Карта Карно — графический способ представления булевых функций с целью их удобной и наглядной ручной минимизации. Является одним из эквивалентных способов описания или задания логических функций наряду с таблицей истинности или выражениями булевой алгебры. Преобразование карты Карно в таблицу истинности и обратно осуществляется элементарным алгоритмом.

Удобство и наглядность такого представления логической функции обусловлено тем, что логические термы, к которым могут быть применены операции попарного неполного склеивания и элементарного поглощения группируются в карте Карно в виде визуально очевидных прямоугольных массивов, содержащих в своих ячейках одинаковые значения (нули и единицы).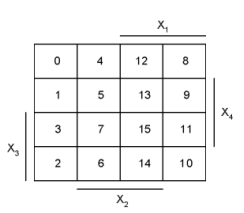



Рисунок 2 - Карта Карно для функции четырех переменных

X1X2 \ X3 X4	00	01	11	10
00	1	*	0	1
01	1	0	*	1
11	1	0	*	1
10	0	0	0	0

Рисунок 3 - Карта Карно комбинационной схемы
Объединим полученные значения и составим формулу

---

, по которой представим схему подключения входных напряжений.

X1X2 \ X3 X4	00	01	11	10
00	1	*	0	1
01	1	0	*	1
11	1	0	*	1
10	0	0	0	0

Рисунок 4 - Карта Карно комбинационной схемы с объединением в массивы

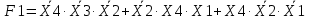(2)

Схема подключения входных сигналов Х с последующим преобразованием их в выходной сигнал F1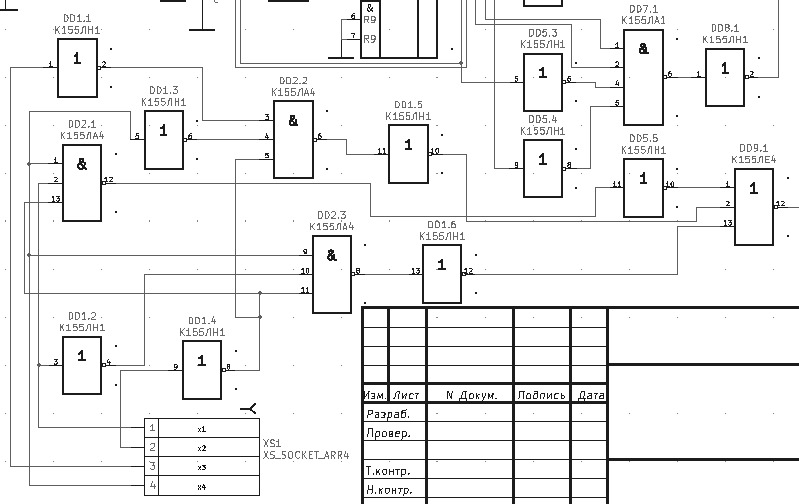



Рисунок 5 - Схема подключения комбинационной схемы

2 Формирователь тактовых импульсов.

Сделаем тоже самое для формирователя тактовых импульсов. Как указано в задании, устройство должно обеспечивать работу на тактовых импульсах 2-4, составим таблицу истинности.

Таблица 2 - Таблица истинности формирователя тактовых интервалов

№такта	Выходы счетчика				F1
	Q4	Q3	Q2	Q1
0	0	0	0	0		0
1	0	0	0	1		0
2	0	0	1	0		0
3	0	0	1	1		0
4	0	1	0	0		1
5	0	1	0	1		1
6	0	1	1	0		1
7	0	1	1	1		0
8	1	0	0	0		0
9	1	0	0	1		0
10	1	0	1	0		0
11	1	0	1	1		*
12	1	1	0	0		*
13	1	1	0	1		*
14	1	1	1	0		*
15	1	1	1	1		*

---

Составим карту Карно для таблицы 2.

Q4Q3 \ Q2Q1	00	01	11	10
00	0	1	*	0
01	0	1	*	0
11	0	0	*	*
10	0	1	*	0

Рисунок 6. Карта Карно формирователя тактовых импульсов

Выделим значения равные единице для того, чтобы составить формулу подключения.

Q4Q3 \ Q2Q1	00	01	11	10
00	0	1	*	0
01	0	1	*	0
11	0	0	*	*
10	0	1	*	0

Рисунок 7. Карта Карно формирователя тактовых импульсов с объединением в массивы

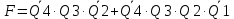(3)

Далее представим схему подключения сигналов выходных сигналов счетчика.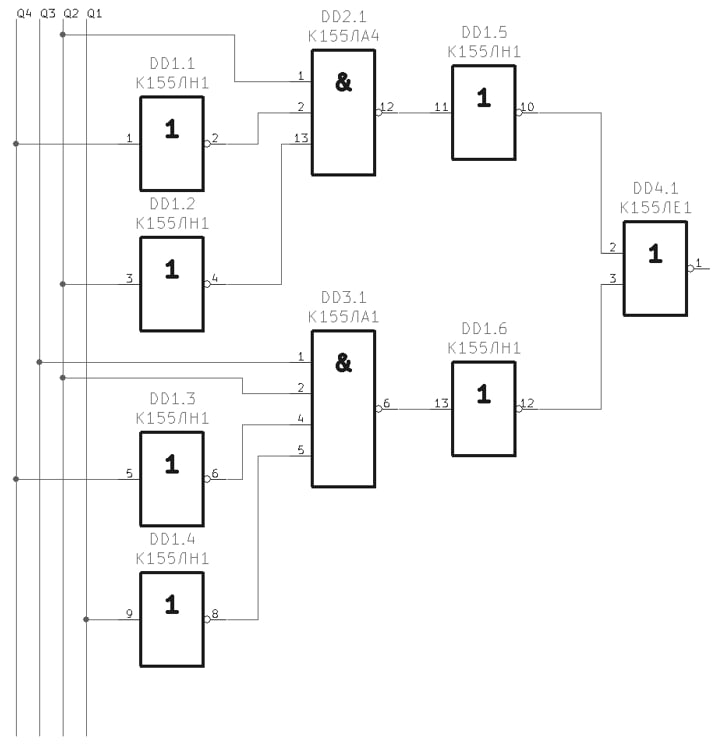



Рисунок 8 - Схема подключения выходных сигналов счетчик

3 Синтезирование счетчика

Теперь синтезируем синхронный счетчик с асинхронным сбросом на базе JK триггеров. Счетчик имеет 15 устойчивых состояний. Счетчик начинает счет со значения «0000», конечное состояние счетчика «1110». При поступлении следующего тактового импульса схема сброса сформирует активный логический уровень и счетчик перейдет в начальное состояние. Возьмем счетчик К155ИЕ2.

---

Смотрите также файлы

• Руководитель решил мотивировать своего сотрудника, предложив ему новую творческую задачу, выполнение которой будет способствовать его более полной самореализации.docx

• Задача 7 Ответ.doc

• Пневмония Пневмония Пневмония.pdf

• Не очень чистых.docx

• На севере Европы.docx