8

Содержание:

Введение

1 Рассчитываем среднюю наработку на отказ………………………………….4

2 Составляем ряд распределения………………………………………………..6

3 Рассчитываем среднее значение выборки 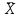…………………………………6

4 Определяем дисперсию выборки Д и среднее

квадратичное отклонение σ……………………………………………………..7

5 Рассчитываем коэффициент вариации……………………………………......7

6 Определяем закон распределения наработки между отказами……………..7

7 Проверка статистической гипотезы…………………………………………..8

8 Определить показатели безотказности……………………………………….10

9 Построение кривой вероятности безотказности работы……………………11

10 Расчет вероятности отказа машины…………………………………………12

11 Определение значение коэффициента готовности…………………………13

Контрольные вопросы…………………………………………………………...14

Список литературы.

Ведение

Надёжность является комплексным свойством изделия, которое включает безотказность, долговечность, ремонтопригодность и сохраняемость.

Надежность — свойство объекта сохранять во время эксплуатации, в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных условиях применения, технического обслуживания, ремонтов, хранения и транспортировки.

Тем самым производство неразрывно связано с проблемой обеспечения надежности эксплуатируемой техники. Надежность, как важнейший показатель качества машин, формируется на всех этапах конструирования, изготовления, эксплуатации и ремонта.

---

По Российским стандартам надежность машин определяется четырьмя свойствами:

- безотказностью;

- долговечностью;

- ремонтопригодностью;

- сохраняемостью.


1 Рассчитываем среднюю наработку на отказ.
Таблица 1 –Шиномонтажный комплект

№ Объекта	Наработка между отказами Т, ч
1	40	5	35	65	35	0	5	0	20	25	15	25	145	20	35	60
2	5	150	30	0	0	100	40	25	30	20	15	15
3	0	75	90	90	55	30	30	20	20	25	65
4	165	15	15	160	30	50	65	25		180
5	5	20	20	25	30	10	0	75	30
6	10	40	20	0	60	20	0	15	55	40	30	60	45
7	70	40	45	15	25	35	0	60	30	10	45	5	60
8	30	45	15	10	30	50	40	45	40	120	20	10	40
9	5	10	60	45	100	15	45	40	45	30	20	45	80	25	50

---

Таблица 2 - Поток отказов.

Наработка	февраль	март		апрель		май			октябрь		Ноябрь
	70	75 ч	80ч	75 ч	75	75 ч	80 ч	75 ч		75
Количество отказов на период	12	15	14	14	13	14	13	15		14

Продолжительность сменной работы - 5 часов.

Суммарное время восстановления отказов – 175часов

В задании даны наработка каждой машины между её отказами. Наработка между отказами является случайной величиной. Для описания случайной величины рассчитываются статические характеристики, и определяется вид закона ее распределения.

Статистическими характеристиками являются:

- среднее значение случайной величины ;

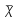- дисперсия Д;

- коэффициент вариации V.
Таблица 3 - Сводные данные расчетных значений статистических

характеристик.

№ интервала	Границы интервала, Ха, Хб	Середина интервала, Хср	Частота в интервале, ni					Частность
1	2	3	4	5	6	7	8	9
1	0-18	9	31	279	-30,58	935,13	28989,03	0,274
2	18-36	27	36	972	-12,58	158,25	5697	0,318
3	36-54	45	21	945	5,42	29,37	616,77	0,186
4	54-72	63	12	756	23,42	548,49	6581,88	0,106
5	72-90	81	5	405	41,42	1715,61	8578,05	0,044
6	90-108	99	2	198	59,42	3530,73	7061,46	0,018
7	108-126	117	1	117	77,42	5993,85	5993,85	0,009
8	126-144	135	0	0	95,42	9104,97	0	0
9	144-162	153	3	459	113,42	12864,09	38592,27	0,027
10	162-180	171	2	342	131,42	17271,21	34542,42	0,018

---

2 Составляем ряд распределения.

Для упрощения расчета численные значения случайной величины разбиваем на 10 интервалов.

Ширина интервала равна:

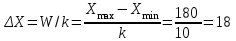(1)

где: W = x_max - x_min - размах выборки;

Xmax - Xmin - максимальные и минимальные значения случайной величины в выборке;

к - число интервалов.

В колонку 2 таблицы 3 записываем границы интервалов в порядке возрастания случайной величины. То есть составляется ряд распределения.
3 Рассчитываем среднее значение выборки .
Для этого в каждом интервале определяется среднее значение интервала. Подсчитывается частота n_i попадания случайных величин в интервал. При этом, если значения попадает на границу двух интервалов его нужно отнести к левому интервалу.

Среднее значение выборки определяется по формуле:

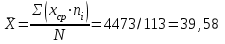(2)

где: Xcpi - середина i-ro интервала;

n_i - число случаев в i-том интервале;





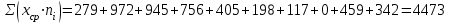
^{k – число интервалов;}

Среднее значение выборки и является средней наработкой на отказ Т_о.

4 Определяем дисперсию выборки Д и среднее квадратичное отклонение σ.
Дисперсия случайной величины характеризует ее рассеивание около математического ожидания. Для выборки объемом N дисперсия определяется по формуле:

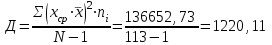(3)

В соответствии с этой формулой для каждого интервала рассчитывается разность (x_cр-x) и заполняется последовательно колонки 6, 7 и 8 таблицы 3. числитель формулы 3 является суммой всех значений в колонке 8 таблицы 3.

Среднее квадратическое отклонение равно квадратному корню из дисперсии т.е.

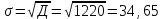(4)

Размерность среднего квадратического отклонения совпадает с размерностью случайной величины.
5 Рассчитываем коэффициент вариации.

---

Числовое значение коэффициента вариации:

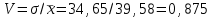(5)
6 Определяем закон распределения наработки между отказами.
Закон распределения характеризует связь между значениями случайной величины и соответствующими вероятностями. Случайные величины, используемые для оценки показателей надежности, наиболее часто подчиняются нормальному, экспоненциальному или распределению Вейбулла.

Построение гистограммы эмпирического распределения и выдвижение

статистической гипотезу.

Гистограмма распределения строится по результатам расчета статистической вероятности. Статистической вероятностью является частность:

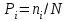(6)

где: n_i – число случаев i – ом интервале;

N – объём выборки.

Значение Р заносится в колонку 9 таблицы 3.

При построении гистограммы по оси абсцисс откладываем интервалы (берутся из таблицы 3) и на каждом интервале строят прямоугольники, высота которых равна Р. Масштаб по оси ординат выбирается в зависимости от максимального значения Р.



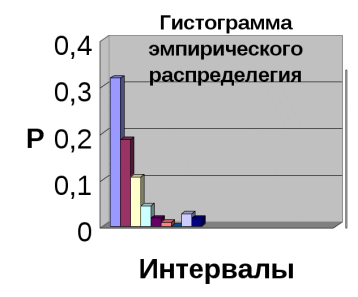
По виду гистограммы, с учетом коэффициента вариации V=0,875 выдвигаем статистическую теорию, что вероятным является экспоненциальное распределение.

7 Проверка статистической гипотезы.
Правдоподобие гипотезы оценивается критериями согласия. С помощью критериев определяется, с какой вероятностью эмпирическое распределение согласуется с теоретическим, то есть оценивается сходимостью по вероятности.

Наиболее часто применяется критерий x²Пирсона, который рассчитывается по формуле:

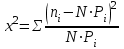₍₇₎



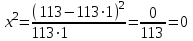
где: k, n_i, N – уравнение 2 таблица 3;

Р_i - теоретическая вероятность в каждом интервале.
Таблица 4 - Расчетные данные для оценки сходимости распределения между отказами машин.

№ п/п	Ха	Хб					Рi
1	2	3	4	5	6	7	8	9	10	11	12
1	0	18	0	0,45	1	0,64	0,274	30,96	0,04	0,0016	0,000052
2	18	36	0,45	0,9	0,64	0,41	0,318	35,93	0,07	0,0049	0,00014
3	36	54	0,9	1,35	0,41	0,26	0,186	21,02	-0,02	0,0004	0,000019
4	54	72	1,35	1,8	0,26	0,17	0,106	11,98	0,02	0,0004	0,000033
5	72	90	1,8	2,25	0,17	0,11	0,044	4,97	0,03	0,0009	0,00018
6	90	108	2,25	2,7	0,11	0,068	0,018	4,32	-2,32	5,38	1,25
7	108	126	2,7	3,15	0,068	0,043	0,009	2,03	-1,03	1,06	0,52
8	126	144	3,15	3,6	0,043	0,028	0	0	0	0	0
9	144	162	3,6	4,05	0,028	0,036	0,027	3,05	-0,05	0,0025	0,0008
10	162	180	4,05	4,5	0,036	0,011	0,018	2,03	-0,03	0,0009	0,00044

---

Смотрите также файлы

• Работа на паре, 29. 03 Join the sentences into one using till, until, if, unless, while, before, after.docx

• Протокол методсовета гбоу спо мо мпт.docx

• Тексты грамот для выпускников начальной школы.docx

• Хейлит Манганотти.docx

• Структура работы.docx