Для получения ВАХ используется электрическая схема подключения ТД, изображенная на рис.3.2. Напряжение, изменяющееся по линейному зако­ну в диапазоне примерно от -0,15В до +1,4В, подается с выхода ВП на иссле­дуемую схему, при этом с помощью того же ВП измеряется падение напряже­ния на измерительном сопротивлении и р-n переходе ТД. Далее полученные данные представляются на графическом индикаторе ВП и обрабатываются.



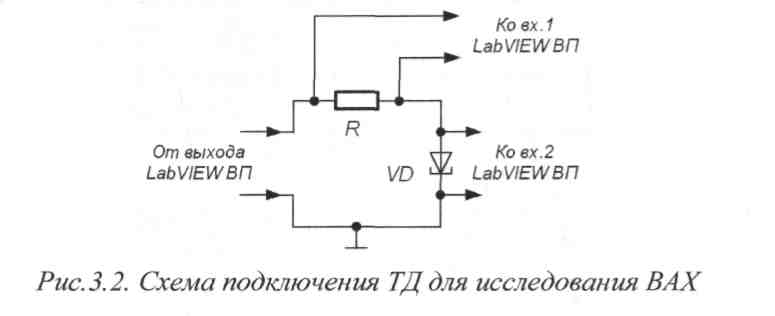
Падение напряжения U_Rна измерительном сопротивлении Rпрямо пропорционально току через ТД, поэтому, откладывая по вертикальной оси графического индикатора ВП напряжение пропорциональное Ur/R, a по горизонтальной оси - напряжение U_Rможно получить на экране изображение ВАХ. Используемый в работе ВП имеет порог чувствительности примерно 0,003 мВ (этот порог определяется характеристиками платы ввода-вывода PCI-6251), в связи с этим необходимо выбрать Rтаким образом, чтобы при протекании через диод пикового тока напряжение на измерительном сопротивлении составляло примерно 1 мВ. На лабораторном стенде установлен AsGa ТД, для которого пиковый ток колеблется в диапазоне от 1 мА до 10 мА, поэтому Rвыбран равным 1 Ом.

Для того, чтобы вычислить электрические характеристики ТД по по­стоянному току можно использовать математическую модель ВАХ, а также графическое или табличное представления ВАХ.

Для определения математической зависимости между током и на­пряжением необходимо в прямоугольной системе координат получить набор отсчетов (x₁,y₁), (х₂,у₂) • • •» (х_n,,у_n). Для получения этого набора в лабо­раторной работе используется LabVIEW BП. Если провести через полу­ченные точки плавную кривую можно наглядно увидеть ВАХ. Существен­ным вопросом является нахождение такой кривой, которая наилучшим

---

способом отвечает полученным данным. Поскольку в эксперименте можно произвольно изменять напряжение U_D, то оно будет являться независимой переменной (х). Соответственно ток I_Dявляется зависимой переменной (у). Для широкого круга задач нахождение математической зависимости, и, со­ответственно, наилучшей кривой, описывающей экспериментальные дан­ные, заключается в нахождении подходящего полинома степени к:

( 3.1)

где b(j) постоянные коэффициенты.

Применительно к рассматриваемой задаче это уравнение принято на­зывать полиномиальной регрессией, а коэффициенты b(j) - коэффициен­тами регрессии.

Для нахождения коэффициентов регрессии в лабораторной работе ис­пользуется специальная процедура, осуществляемая в среде LabVIEW. Рас­четы начинают для модели, которая обладает самой простой структурой и, по мнению экспериментатора, может обеспечить согласие между значениями зависимой переменной y(i), измеренными в эксперименте, и вычисленными по уравнению регрессии значениями h(i). Для оценки качества модели ис­пользуется специальная статистическая процедура, называемая проверкой адекватности модели. Модель адекватна, если оценка дисперсии относи­тельно регрессии SS(ocm), и независимая от нее оценка дисперсии случайных возмущений SS(e), оказывающих влияние на результаты измерений отклика, статистически неотличимы друг от друга. Оценка значения SS(ocm) прово­дится при построении регрессионной модели по формуле:

---

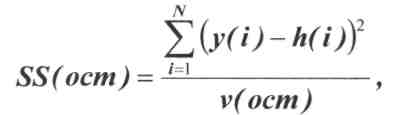
(3.2)

где N- общее число наблюдений;

v(ocm) = N -k-1 - число степеней свободы остаточной суммы квадратов.

уi – результату i-ого наблюдения;

h(i) — значение отклика, вычисленное по уравнению регрессии.

О 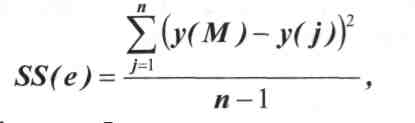ценка значения SS(e) проводится по результатам специальной се­рии независимых наблюдений по формуле:

(3.3)

где уj - результату j-ого наблюдения;



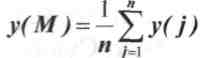
- среднее значение результатов наблюдений;

n - общее число независимых наблюдении.

Эта серия наблюдений выполняется при неизменных условиях и при фиксированном значении независимой переменной х, поэтому на результатах измерения уjсказывается только влияние случайных возмущений. При выполнении серии независимых наблюдений количество опытов n и значение переменной х: выбирает экспериментатор. Если закон распределения величины уф предполагается нормальным, то достаточно, как правило, 10 -15 опытов.

Собственно процедура проверки адекватности заключается в вычис­лении дисперсионного отношения F=SS(ocm)/SS(e) и сравнении полученного результата с табличным значением F, функции распределения Фишера.

Величина F имеет распределение Фишера с v(ocm) = N-k-1 и v(e) = п-1 степенями свободы. Для заданного уровня значимости, а по таблице распределения Фишера с v(ocm) и v(e) степенями свободы находят величи­

---

ну Fi=F(a,v(ocm), v(e)). Если F< F_t, то гипотеза о статистическом равенстве S_ocmи SS(e) не отвергается и модель признается адекватной, если F> F_tмодель считается неадекватной.

Данная процедура может быть реализована, если SS(ocm)>SS(e), в противном случае вычисляется обратное дисперсионное соотношение:



(3/4)

а для нахождения F_tпользуются таблицей распределения Фишера с

v(e) = п-1 и v(ocm) — N-k-1 степенями свободы. Выводы, которые при

этом делаются, аналогичны предыдущим.

Как правило, при выполнении экспериментальных исследований в

технике уровень значимости, а принимается равным 0,05.

Если первоначально выбранная модель окажется неадекватной, структуру модели усложняют, повышая степень полинома на единицу. Данные обрабатывают снова, получают новые оценки коэффициентов рег­рессии и вновь проверяют гипотезу об адекватности. Эта процедура вы­полняется до тех пор, пока не получится удовлетворительное согласование экспериментальных данных и результатов расчетов по модели.

Для получения координат локальных экстремумов (точки 1 и 2, рис.3.1) адекватную модель анализируют стандартными математическими методами. Значение находят из уравнения:

(3.5)

которое в заданном диапазоне изменения величины Uимеет 2 действи­тельных корня (точки 1 и 3, рис.3.1). Эти операции удобно выполнять на компьютере с помощью одного из стандартных пакетов для математиче­ской обработки данных.

ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА

В

---

состав лабораторного стенда входят:

• 
  базовый лабораторный стенд.
  
• 
  Лабораторный модуль Lab3A для исследования ВАХ туннельного диода типа АИ101.
  

РАБОЧЕЕ ЗАДАНИЕ

Подготовьте шаблон отчета в редакторе MS Word.

Установите лабораторный модуль Lab3A на макетную плату лабора­торной станции NI ELVIS. Внешний вид модуля показан на рис.3.3.

При исследовании ВАХ туннельного диода используется схема, изо­браженная на рис.3.4



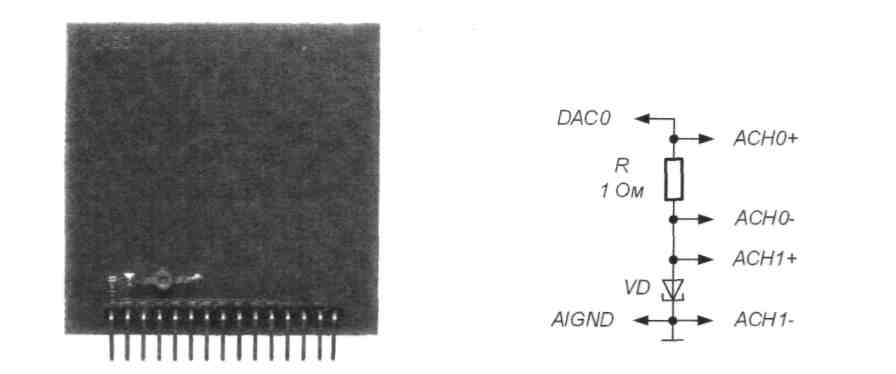
Рис. 3.3. Внешний вид модуля LаbЗА Рис. 3.4. Принципиальная электри-
для исследования ВАХ туннельного ческая схема для исследования ВАХ
диодатуннельного диода

Загрузите и запустите программу Lab-3.vi.

После ознакомления с целью работы нажмите кнопку «Начать работу». На экране появится изображение ВП, необходимого для выполнения задания 1 (рис. 3.5).



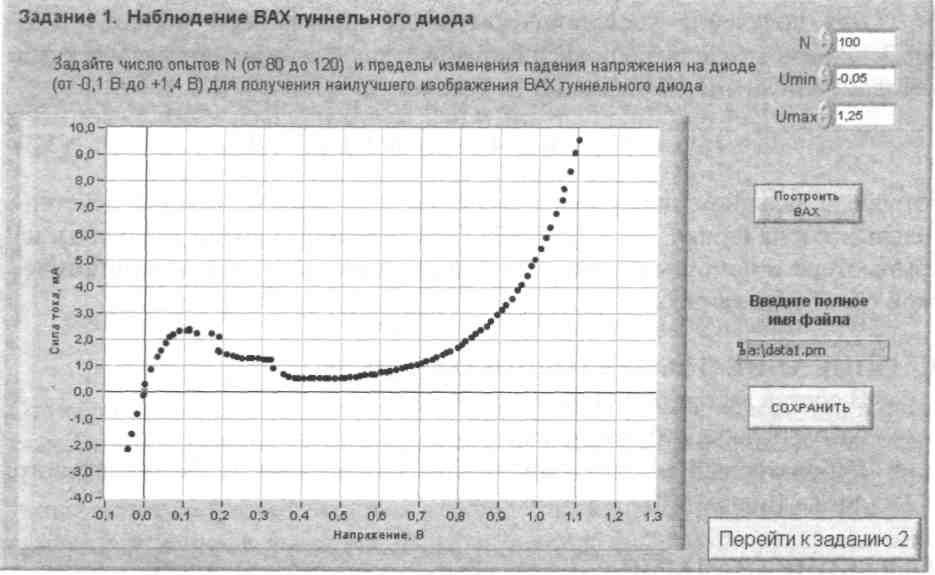
Рис. 3.5. Лицевая панель ВП при выполнении задания 1

Задание 1. Наблюдение ВАХ туннельного диода.

ВП дает возможность получить набор зависимостей между напряже­нием на ТД и током через него. Полученные данные ВП позволяет запи­сать в индивидуальный файл пользователя. Каждый студент может полу­чить свой индивидуальный набор экспериментальных данных, выбирая свой диапазон изменения напряжения на ТД и количество эксперимен­тальных точек на ВАХ.

Подготовьте ВП к измерениям, для чего установите в соответствую­щих окнах на передней панели ВП диапазон изменения напряжения и ко­личество экспериментальных точек. При выборе параметров примите во внимание, что нижний предел устанавливаемого напряжения не должен быть ниже -0,1 В, а верхний - выше +1,4 В. Рекомендуемое количество экспериментальных точек лежит в диапазоне от 80 до 120.

1. 
   Проведите измерения, для чего нажмите кнопку «Построить ВАХ» на передней панели ВП. На экране ВП появится набор эксперимен­тальных точек.
   
2. 
   Скопируйте полученный график на страницу отчета.
   

---

Смотрите также файлы

• Расчеты оборудования для добычи нефти.docx

• Разработка элективного курса по астрономии.pdf

• Информатика пнінен бадарламаны тілуі I, ii, ііі, iv тосан. 20222023 о ж.docx

• Вопросы для сравнения.docx

• Методическое пособие для подготовки по профессии Оператор товарный.pdf