Файл: Контрольные вопросы по курсу " Дискретная математика".docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО КУРСУ
“Дискретная математика” направления ПРИКЛАДНАЯ ИНФОРМАТИКА
з/о, I курс, 2 семестр 2021/2022
учебного года
-
Центр дерева.
Свободные деревья выделяются из других графов тем, что их центр всегда оправдывает своё название.
ТЕОРЕМ А Центр свободного дерева состоит из одной вершины или из двух смежных вершин:
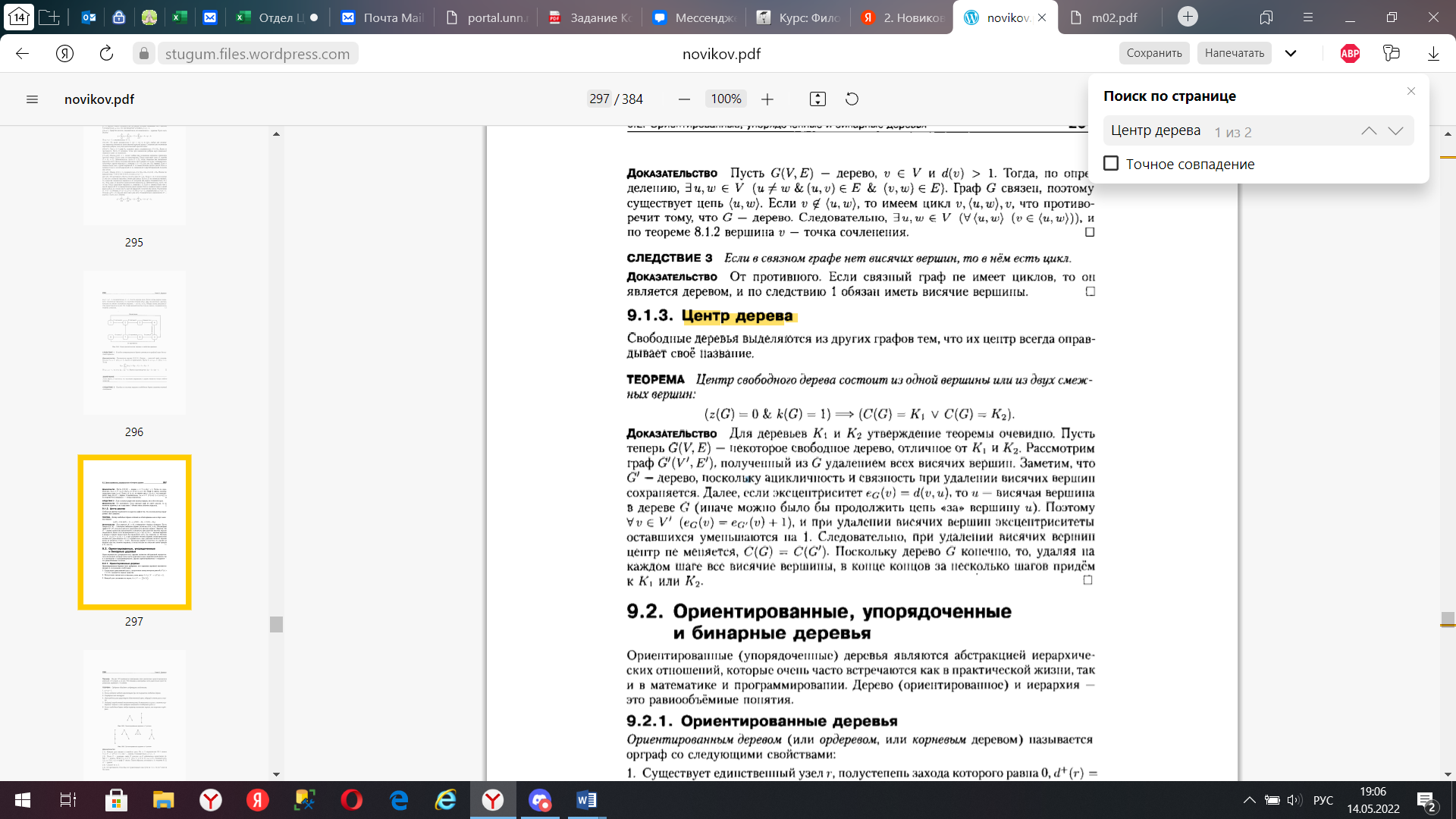
ДОКАЗАТЕЛЬСТВО ДЛЯ деревьев Ki и К2 утверждение теоремы очевидно. Пусть теперь G(V, Е) — некоторое свободное дерево, отличное от Ki и К2. Рассмотрим граф G'(V', Е'), полученный из G удалением всех висячих вершин. Заметим, что G' — дерево, поскольку ацикличность и связность при удалении висячих вершин сохраняется. Далее, если эксцентриситет ec(v) = d(v,u), то и — висячая вершина в дереве G (иначе можно было бы продолжить цепь «за» вершину и). Поэтому \/г> б V' (ec(v) = ес('о) + 1), и при удалении висячих вершин эксцентриситеты оставшихся уменьшаются на 1. Следовательно, при удалении висячих вершин центр пе меняется, C(G) = C(G'). Поскольку дерево G конечно, то, удаляя на каждом шаге все висячие вершины, в конце концов за несколько шагов придём к К1 или К2.
-
Алгоритмы построения основного дерева графа.
Алгоритм Крускала имеет следующий вид:
-
Выбрать в графе G ребро e минимального веса, не принадлежащее множеству E и такое, что его добавление в E не создает цикл в дереве T
-
Добавить это ребро во множество ребер E.
-
Продолжить, пока имеются ребра, обладающие указанными свойствами.
Алгоритм Прима имеет следующий вид:
Всегда имеется дерево, к которому ребра добавляют до тех пор, пока не получится остовное дерево. Используя алгоритм Прима, сначала выбираем вершину v0 графа G, а затем выбираем ребро с наименьшим весом e1 = {v0 ,v1}, инцидентное к вершине v0 и формируем дерево Т1.
Следующим выбираем ребро с наименьшим весом е2 такое, что одна вершина ребра принадлежит дереву T1, а вторая — нет, и добавляем его в дерево, после чего получаем дерево T2 с двумя ребрами.
Сформировав дерево Тk формируем дерево Тk+1, выбирая ребро с минимальным весом ek+1 такое, что одна его вершина принадлежит дереву Тk, а другая — нет, и добавляем это ребро в дерево.
Продолжаем процесс до тех пор, пока дерево не будет содержать все вершины графа G. 1)
Выбрать вершину v0 графа G и ребро с наименьшим весом e1, для которого v0 – одна из вершин, и сформировать дерево T1
2) Для заданного дерева Tk с ребрами e1, e2, e3, …, ek , если имеется вершина, не принадлежащая Tk , выбрать ребро с наименьшим весом, смежное с ребром дерева Tk и имеющее вершину вне дерева Tk . Добавить в дерево Tk , формируя дерево Tk+1.
3) Продолжить, пока имеются вершины графа G, не принадлежащие дереву.
Построение минимального остовного дерева можно проводить двумя способами:
-
остов графа строится непосредственно на самом графе, выделяя ребра утолщенной линией, которые входят в остовное дерево;
-
строится отдельно корневое дерево, которое будет минимальным остовным деревом. Второй случай используется, если требуется определить высоту построенного дерева.
-
Алгоритм Краскала построения минимального остовного дерева.
Алгоритм Краскала - это алгоритм минимального остовного дерева, что принимает граф в качестве входных данных и находит подмножество ребер этого графа, который формирует дерево, включающее в себя каждую вершину, а также имеет минимальную сумму весов среди всех деревьев, которые могут быть сформированы из графа.
Он подпадает под класс алгоритмов, называемых «жадными» алгоритмами , которые находят локальный оптимум в надежде найти глобальный оптимум.
Мы начинаем с ребер с наименьшим весом и продолжаем добавлять ребра, пока не достигнем нашей цели.
Шаги для реализации алгоритма Краскала следующие:
-
Сортировать все ребра от малого веса до высокого.
-
Возьмите ребро с наименьшим весом и добавьте его в остовное дерево. Если добавление ребра создало цикл, то отклоните это ребро.
-
Продолжайте добавлять ребра, пока не достигнете всех вершин.
-
Алгоритм Прима построения минимального остовного дерева.
Алгоритм Прима - это алгоритм минимального остовного дерева, что принимает граф в качестве входных данных и находит подмножество ребер этого графа, который формирует дерево, включающее в себя каждую вершину, а также имеет минимальную сумму весов среди всех деревьев, которые могут быть сформированы из графа.
Он подпадает под класс алгоритмов, называемых «жадными» алгоритмами , которые находят локальный оптимум в надежде найти глобальный оптимум.
Мы начинаем с одной вершины и продолжаем добавлять ребра с наименьшим весом, пока не достигнем нашей цели.
Шаги для реализации алгоритма Прима следующие:
-
Инициализируйте минимальное остовное дерево с произвольно выбранной вершиной.
-
Найдите все ребра, которые соединяют дерево с новыми вершинами, найдите минимум и добавьте его в дерево.
-
Продолжайте повторять шаг 2, пока не получите минимальное остовное дерево.
-
Деревья с корнем.
-
Произвольно зафиксируем некоторую вершину 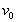 дерева
дерева 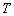 и назовем ее корнем дерева. Само дерево в этом случае будем называть деревом с корнем или корневым деревом.
и назовем ее корнем дерева. Само дерево в этом случае будем называть деревом с корнем или корневым деревом.
-
Иногда полезно, руководствуясь какими–либо соображениями, выделять в дереве 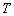 некоторую определенную цепь
некоторую определенную цепь 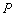 , которую обычно называют стволом дерева. Корень дерева обычно является одной из концевых вершин ствола. Каждая концевая вершина дерева
, которую обычно называют стволом дерева. Корень дерева обычно является одной из концевых вершин ствола. Каждая концевая вершина дерева 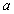 связана с ближайшей вершиной
связана с ближайшей вершиной 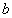 ствола единственной цепью. Эту цепь называют ветвью дерева, выходящей из вершины
ствола единственной цепью. Эту цепь называют ветвью дерева, выходящей из вершины 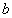 в вершину
в вершину 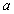 . При отсутствии у дерева ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева с его корнем.
. При отсутствии у дерева ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева с его корнем.
-
Корневые деревья естественно ориентировать, если в этом есть необходимость, от корня. Все ребра, инцидентные корню дерева, считаются исходящими из корня и заходящими в вершины, смежные корню. Все ребра дерева, инцидентные вершинам, удаленным на расстояние 1 от корня, считаются исходящими из этих вершин и заходящими в вершины, им смежные. Процесс ориентации ребер продолжается подобным образом до тех пор, пока не будут ориентированы все ребра дерева. Поученное в результате такой ориентации дерево с корнем называется ориентированным деревом. В нем все ребра имеют направление от корня. Если поменять направления всех дуг ориентированного дерева на противоположные (к корню), то получившийся в итоге ориентированный граф называют сетью сборки.
6. Двоичные деревья. Двоичное дерево поиска.
Двоичным деревом поиска (ДДП) называют дерево, все вершины которого упорядочены, каждая вершина имеет не более двух потомков (назовём их левым и правым), и все вершины, кроме корня, имеют родителя. Вершины, не имеющие потомков, называются листами.
• Подразумевается, что каждой вершине соответствует элемент или несколько элементов, имеющие некие ключевые значения, в дальнейшем именуемые просто ключами.
• ДДП позволяет выполнять следующие основные операции:
▫ Поиск вершины по ключу.
▫ Определение вершин с минимальным и максимальным значением ключа.
▫ Переход к предыдущей или последующей вершине, в порядке, определяемом ключами.
▫ Вставка вершины.
▫ Удаление вершины.
Двоичное дерево может быть логически разбито на уровни. Корень дерева является нулевым уровнем, потомки корня – первым уровнем, их потомки – вторым, и т.д. Глубина дерева это его максимальный уровень.
• Каждую вершину дерева можно рассматривать как корень поддерева, которое определяется данной вершиной и всеми потомками этой вершины, как прямыми, так и косвенными. Поэтому о дереве можно говорить как о рекурсивной структуре.
-
Алгоритм Дейкстры нахождения кратчайших путей в нагруженном орграфе.
Алгоритм Дейкстры позволяет найти кратчайшие пути от данной вершины до всех остальных вершин в графе. Алгоритм состоит из следующих шагов:
-
Положить для всех вершин (кроме исходной) расстояние dist(v) = INF, для исходной dist(start) = 0
-
Выбрать непомеченную вершину v, с минимальным расстоянием. Если такой вершины нет, то завершить работу
-
Пометить v
-
Для всех непомеченных вершин, смежных с v, попытаться улучшить оценку расстояния
-
Вернуться к шагу 2
-
Эйлеровы графы. Условие существования Эйлеровых циклов.
Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом. Если граф имеет цепь (не обязательно простую), содержащую все ребра графа по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.
Рассмотрим алгоритм построения эйлерова цикла в эйлеровом графе.
Алгоритм Флери.
Начиная с произвольной вершины, идем по ребрам графа, соблюдая следующие правила:
1. Удаляем ребра по мере их прохождения, и удаляем также изолированные вершины, которые при этом образуются.
2. Идем по мосту только тогда, когда нет других возможностей.
По теореме граф является эйлеровым. На диаграмме ребра пронумерованы в порядке их прохождения, таким образом эйлеров цикл abcdf edbeca.
-
Алгоритм построения Эйлерова цикла в графе.
Алгоритм нахождения эйлерова цикла.
-
Выбрать произвольную вершину А
-
Выбрать произвольно некоторое ребро, инцидентное вершине А, и присвоить ему номер 1. Это ребро называется помеченным
-
Каждое пройденное ребро вычеркиваем и присваиваем ему номер на 1 больше предыдущего пройденного ребра
-
Находясь в вершине X, не выбираем ребра, соединяющие вершину X с вершиной А, если есть возможность другого выбора
-
Находясь в вершине X, не выбираем рёбра, являющиеся мостом
-
После того как в графе пронумерованы все ребра, цикл образован ребрами с номерами от 1 до n, который является эйлеровым
-
Гамильтоновы графы.
Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Если граф имеет простую цепь, содержащую все вершины графа по одному разу, то такая цепь называется гамильтоновой цепью, а граф называется полугамильтоновым графом.
-
Задача коммивояжера и способы ее решения.
Задача коммивояжера — пожалуй, одна из самых известных оптимизационных задач. Ее цель заключается в нахождении самого выгодного маршрута (кратчайшего, самого быстрого, наиболее дешевого), проходящего через все заданные точки (пункты, города) по одному разу, с последующим возвратом в исходную точку. Условия задачи должны содержать критерий выгодности маршрута (т. е. должен ли он быть максимально коротким, быстрым, дешевым или все вместе), а также исходные данные в виде матрицы затрат (расстояния, стоимости, времени и т. д.) при перемещении между рассматриваемыми пунктами. Особенности задачи в том, что она довольно просто формулируется и найти хорошие решения для нее также относительно просто, но вместе с тем поиск действительно оптимального маршрута для большого набора данных — непростой и ресурсоемкий процесс. Для решения задачи коммивояжера ее надо представить как математическую модель. При этом исходные условия можно записать в формате матрицы — таблицы, где строкам соответствуют города отправления, столбцам — города прибытия, а в ячейках указываются расстояния (время, стоимость) между ними; или в виде графа — схемы, состоящей из вершин (точек, кружков), которые символизируют города, и соединяющих их ребер (линий), длина которых соответствует расстоянию между городами. Виды задачи коммивояжера по симметричности ребер графа: симметричная (англ. «Symmetric TSP») — все пары ребер, соединяющих одни и те же вершины, имеют одинаковую длину (т. е. граф, представляющий исходные данные задачи, является неориентированным). Иными словами, длина прямого пути от города A до города B и длина обратного пути от города B до города A, одинаковы. То же самое справедливо и в отношении остальных пар городов (A-C и C-A, B-C и C-D, и т. д.); асимметричная (англ. «Asymmetric TSP») — длина пар ребер соединяющих одни и те же города, может различаться (ориентированный граф). Для этого типа задачи коммивояжера прямой путь, например, из города A в город B может быть короче или длиннее обратного пути из города B в город A. Такое может быть не только в теории, но и в реальности — в случае дорог с односторонним движением. Кроме того, в общем случае поиска кратчайшего пути охватывающего набор пунктов, которые требуется посетить по одному разу, говорят об обобщенной задаче коммивояжера (англ. «Generalized TSP»). Типы задачи коммивояжера по замкнутости маршрута: замкнутая — нахождение кратчайшего пути, проходящего через все вершины по одному разу с последующим возвратом в точку старта (маршрут получается замкнутым, закольцованным); незамкнутая — нахождение кратчайшего пути, проходящего через все вершины по одному разу и без обязательного возврата в исходную точку (маршрут получается разомкнутым). Можно предложить и другие классификации задачи коммивояжера (например, метрическая и неметрическая), но в данном случае не стоит перегружать ими статью. В этой статье мы рассматриваем алгоритм решения именно для замкнутого варианта задачи (т. е. с возвратом в исходную точку). Методы решения задачи коммивояжера довольно разнообразны и различаются применяемым инструментарием, точностью находимого решения и сложностью требуемых вычислений. Вот лишь некоторые из них: полный перебор (метод «грубой силы», англ. «Brute Force») — заключается в последовательном рассмотрении всех возможных маршрутов и выборе из них оптимального. Метод самый простой и точный, но неэффективный и при большом количестве городов его применение становится затруднительным ввиду значительных затрат времени и ресурсов на перебор огромного количества вариантов решения задачи. Для ускорения и повышения эффективности полного перебора используются различные приемы: метод ветвей и границ, параллельные вычисления, радужные таблицы; случайный перебор — в этом случае вычисляются не все возможные варианты маршрута, а лишь некоторые выбранные в случайном порядке (например, с помощью генератора случайных чисел). Из рассмотренных вариантов затем выбирается наилучший. Конечно, вероятнее всего полученное решение не будет оптимальным (впрочем, оно не будет и самым худшим), но зато данный метод требует меньших затрат времени и вычислительных ресурсов, а потому в некоторых случаях его применение оправдано; динамическое программирование — ключевая идея заключается в вычислении и запоминании пройденного пути от исходного города до всех остальных, последующем прибавлении к нему расстояний от текущих городов до оставшихся, и так далее. По сравнению с полным перебором этот метод позволяет существенно сократить объем вычислений; жадные алгоритмы (англ. «Greedy») — основаны на нахождении локально оптимальных решений на каждом этапе вычислений и допущении, что найденное таким образом итоговое решение будет глобально оптимальным. Т. е. на каждой итерации выбирается лучший участок пути, который включается в итоговый маршрут. Метод простой, но его большой недостаток в том, что может возникнуть ситуация, когда окажется, что начальная и конечная точки маршрута разнесены далеко друг от друга и их придется соединять длинным отрезком пути, что значительно снизит эффективность решения. К жадным алгоритмам относятся: метод ближайшего соседа (англ. «Nearest Neighbour»), модифицированный метод ближайшего соседа (англ. «Double Ended Nearest Neighbour»), метод самого дешевого включения и т. д.; метод минимального остовного дерева — поиск маршрута ведется на графе. Для нахождения оптимального пути применяются различные инструменты: алгоритм Прима, алгоритм Краскала, алгоритм Борувки; метод имитации отжига — один из численных методов Монте-Карло; метод эластичной сети — каждый из возможных маршрутов рассматривается как отображение окружности на плоскость; муравьиный алгоритм — эвристический метод, основанный на моделировании поведения муравьев, ищущих пути от своей колонии к источникам пищи. Первую версию такого алгоритма предложил доктор наук Марко Дориго в 1992 году. Этот метод позволяет относительно быстро найти хорошее, но не обязательно оптимальное решение; генетический алгоритм — еще один эвристический метод, заключающийся в случайном подборе и комбинировании исходных параметров с использованием механизмов имитирующих естественный отбор в процессе эволюции (наследование, мутации, кроссинговер). Несмотря на довольно широкие возможности применения (и не только в логистике), этот метод часто становится объектом критики; метод ветвей и границ — один из методов дискретной оптимизации, являющийся развитием метода полного перебора, но отличающийся от него отсевом в процессе вычисления подмножеств неэффективных решений.
-
Алгебра логики.
Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.
Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями: Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.
Логические выражения могут быть простыми и сложными.
Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь».
Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.
В качестве основных логических операций в сложных логических выражениях используются следующие:
• НЕ (логическое отрицание, инверсия);
• ИЛИ (логическое сложение, дизъюнкция);
• И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение — двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например:
-
таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции;
-
в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции;
-
если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов.
-
Способы задания логических функций.
Определение. Функция f(x0, x1, …, xn) называется логической (булевой), если ее аргументы x0, x1, …, xn и значения функции могут принимать только два значения: логического 0 и логической 1.
Для задания функции алгебры логики, как и любой другой функции необходимо поставить в соответствие значения функции для всех возможных комбинаций входных аргументов. Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n.
Способы задания логических функций
1. Словесный. Взаимосвязь значений функции и ее аргументов описывается словесной формулировкой.
2. Табличный. При табличном способе строится таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов. В отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов.
3. Цифровой. Функцию алгебры логики определяют в виде последовательности десятичных чисел. При этом последовательно расписывают эквиваленты двоичных кодов, которые соответствуют единичным либо нулевым значениям функции.
4. Аналитический. Функция алгебры логики записывается в виде аналитического выражения, где показаны логические операции, выполняемые над аргументами функции.
13.Существенные и фиктивные переменные логических функций.
Определение 1. Функция f(x1, x2, … xi-1, xi, xi+1, … xn) существенно зависит от переменной xi, если у переменных x1, …, xi-1, xi+1, …xn существует такой набор значений α1, …, αi-1, αi+1, …αn, что выполняется неравенство: f(α1, α2, … αi-1, 0, αi+1, … αn) ≠ f(α1, α2, … αi-1, 1, αi+1, … αn). В этом случае переменную xi называют существенной. Если же xi не является существенной, то ее называют фиктивной.
Определение 2. Переменную xi называют фиктивной, если для любого набора значений α1, …, αi-1, αi+1, …αn переменных x1, …, xi-1, xi+1, …xn выполняется равенство: f(α1, α2, … αi-1, 0, αi+1, … αn) = f(α1, α2, … αi-1, 1, αi+1, … αn).
-
Логические функции одной и двух переменных.
Логической функцией называют функцию F (Х1, Х2, ..., Х n), аргументы которой Х 1, Х 2, ..., Х n и сама функция принимают значения 0 или 1. Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции.
-
Суперпозиция логических функций.
это функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных. Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.
-
Законы алгебры логики.
1. Закон тождества
Х = Х
Всякое высказывание тождественно самому себе.
2. Закон исключенного третьего
X \/ ¬X = 1
Высказывание может быть либо истинным, либо ложным, третьего не дано. Следовательно, результат логического сложения высказывания и его отрицания всегда принимает значение «истина».
3. Закон непротиворечия
X/\ ¬X = 0
Высказывание не может быть одновременно истинным и ложным. Если высказывание Х истинно, то его отрицание НЕ Х должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
4. Закон двойного отрицания
¬¬X = X
Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.
5. Переместительный (коммутативный) закон
X /\ Y = Y /\ X
X /\ Y = YX
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
6. Сочетательный (ассоциативный) закон
(X \/Y) \/Z = X \/ (Y \/Z)
(X/\Y)/\Z=X/\(Y/\Z)
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
5. Распределительный (дистрибутивный) закон
(X /\ Y) \/ Z= (X /\ Z) \/ (Y /\ Z)
(X /\ Y) \/ Z = (X \/ Z) /\ (Y \/ Z)
Определяет правило выноса общего высказывания за скобку.
7. Закон общей инверсии Закон де Моргана
¬(X \/ Y) = ¬X /\ ¬Y
¬(X /\ Y) = ¬X \/ ¬Y
Закон общей инверсии.
8. Закон равносильности (идемпотентности)
A\/A= A;
A/\ A = A.
от латинских слов idem — тот же самый и potens —сильный
9. Законы исключения констант:
A\/ 1 = 1, A\/ 0 = A;
A/\1 = A, A/\0 = 0.
10. Закон поглощения:
A\/ (A/\B) = A;
A/\ (A\/B) = A.
11. Закон исключения (склеивания):
(A/\B) \/ (¬A/\B) = B;
(A\/B)/\(¬A \/B) = B.
12. Закон контрапозиции
(правило перевертывания):
(A<=>B) = (B<=>A).
13. А => В = ¬A \/ В;
14. ¬ (A=>B)=A/\B
15. А <=>В = (А /\ В) \/ (¬A /\ ¬B);
16. А <=>В = (¬A \/ В) /\ (А \/¬B).
17.Функционально полные системы логических функций.
Функционально полная система логических элементов - это такой набор элементов, используя который можно реализовать любую сколь угодно сложную логическую функцию. Поскольку любая логическая функция представляет собой комбинацию простейших функций - дизъюнкции, конъюнкции и инверсии, то набор из элементов трех типов, реализующих соответственно функции И, или и НЕ, естественно, является функционально полным.
18. Дизъюнктивная нормальная форма (ДНФ).
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности.
19. Совершенная дизъюнктивная нормальная форма (СДНФ).
одна из форм представления функции алгебры логики (булевой функции) в виде логического выражения. Представляет собой частный случай ДНФ, удовлетворяющий следующим трём условиям:
-
в ней нет одинаковых слагаемых (элементарных конъюнкций);
-
в каждом слагаемом нет повторяющихся переменных;
-
каждое слагаемое содержит все переменные, от которых зависит булева функция (каждая переменная может входить в слагаемое либо в прямой, либо в инверсной форме).
Любая булева формула, не являющаяся тождественно ложной, может быть приведена к СДНФ, причём единственным образом, то есть для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.
20. Конъюнктивная нормальная форма (КНФ).
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ. Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.
21. Совершенная конъюнктивная нормальная форма (СКНФ).
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
1.в ней нет одинаковых элементарных дизъюнкций
2.в каждой дизъюнкции нет одинаковых пропозициональных переменных
3.каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв
22. Сведение логических формул к ДНФ.
Шаг 1. Все подформулы A вида B C (т.е. содержащие импликацию) заменяем на BVC или на (B&C).
Шаг 2. Все подформулы A вида B
C (т.е. содержащие эквивалентность) заменяем на (A&B) V (A&B) или на (AVB)&(AVB).
Шаг 3. Все отрицания, стоящие над сложными подформулами, опускаем по законам де Моргана.
Шаг 4. Устраняем все двойные отрицания над формулами (в соответствии с равносильностью 8).
+Шаг 5. Осуществляем раскрытие всех скобок по закону дистрибутивности конъюнкции относительно дизъюнкции для ДНФ
-
Приведение ДНФ к СДНФ.
КОНТРОЛЬНЫЕ ВОПРОСЫ ПО КУРСУ
“Дискретная математика” направления ПРИКЛАДНАЯ ИНФОРМАТИКА
з/о, I курс, 2 семестр 2021/2022
учебного года
-
Центр дерева.
Свободные деревья выделяются из других графов тем, что их центр всегда оправдывает своё название.
ТЕОРЕМ А Центр свободного дерева состоит из одной вершины или из двух смежных вершин:
ДОКАЗАТЕЛЬСТВО ДЛЯ деревьев Ki и К2 утверждение теоремы очевидно. Пусть теперь G(V, Е) — некоторое свободное дерево, отличное от Ki и К2. Рассмотрим граф G'(V', Е'), полученный из G удалением всех висячих вершин. Заметим, что G' — дерево, поскольку ацикличность и связность при удалении висячих вершин сохраняется. Далее, если эксцентриситет ec(v) = d(v,u), то и — висячая вершина в дереве G (иначе можно было бы продолжить цепь «за» вершину и). Поэтому \/г> б V' (ec(v) = ес('о) + 1), и при удалении висячих вершин эксцентриситеты оставшихся уменьшаются на 1. Следовательно, при удалении висячих вершин центр пе меняется, C(G) = C(G'). Поскольку дерево G конечно, то, удаляя на каждом шаге все висячие вершины, в конце концов за несколько шагов придём к К1 или К2.
-
Алгоритмы построения основного дерева графа.
Алгоритм Крускала имеет следующий вид:
-
Выбрать в графе G ребро e минимального веса, не принадлежащее множеству E и такое, что его добавление в E не создает цикл в дереве T -
Добавить это ребро во множество ребер E. -
Продолжить, пока имеются ребра, обладающие указанными свойствами.
Алгоритм Прима имеет следующий вид:
Всегда имеется дерево, к которому ребра добавляют до тех пор, пока не получится остовное дерево. Используя алгоритм Прима, сначала выбираем вершину v0 графа G, а затем выбираем ребро с наименьшим весом e1 = {v0 ,v1}, инцидентное к вершине v0 и формируем дерево Т1.
Следующим выбираем ребро с наименьшим весом е2 такое, что одна вершина ребра принадлежит дереву T1, а вторая — нет, и добавляем его в дерево, после чего получаем дерево T2 с двумя ребрами.
Сформировав дерево Тk формируем дерево Тk+1, выбирая ребро с минимальным весом ek+1 такое, что одна его вершина принадлежит дереву Тk, а другая — нет, и добавляем это ребро в дерево.
Продолжаем процесс до тех пор, пока дерево не будет содержать все вершины графа G. 1)
Выбрать вершину v0 графа G и ребро с наименьшим весом e1, для которого v0 – одна из вершин, и сформировать дерево T1
2) Для заданного дерева Tk с ребрами e1, e2, e3, …, ek , если имеется вершина, не принадлежащая Tk , выбрать ребро с наименьшим весом, смежное с ребром дерева Tk и имеющее вершину вне дерева Tk . Добавить в дерево Tk , формируя дерево Tk+1.
3) Продолжить, пока имеются вершины графа G, не принадлежащие дереву.
Построение минимального остовного дерева можно проводить двумя способами:
-
остов графа строится непосредственно на самом графе, выделяя ребра утолщенной линией, которые входят в остовное дерево; -
строится отдельно корневое дерево, которое будет минимальным остовным деревом. Второй случай используется, если требуется определить высоту построенного дерева.
-
Алгоритм Краскала построения минимального остовного дерева.
Алгоритм Краскала - это алгоритм минимального остовного дерева, что принимает граф в качестве входных данных и находит подмножество ребер этого графа, который формирует дерево, включающее в себя каждую вершину, а также имеет минимальную сумму весов среди всех деревьев, которые могут быть сформированы из графа.
Он подпадает под класс алгоритмов, называемых «жадными» алгоритмами , которые находят локальный оптимум в надежде найти глобальный оптимум.
Мы начинаем с ребер с наименьшим весом и продолжаем добавлять ребра, пока не достигнем нашей цели.
Шаги для реализации алгоритма Краскала следующие:
-
Сортировать все ребра от малого веса до высокого. -
Возьмите ребро с наименьшим весом и добавьте его в остовное дерево. Если добавление ребра создало цикл, то отклоните это ребро. -
Продолжайте добавлять ребра, пока не достигнете всех вершин.
-
Алгоритм Прима построения минимального остовного дерева.
Алгоритм Прима - это алгоритм минимального остовного дерева, что принимает граф в качестве входных данных и находит подмножество ребер этого графа, который формирует дерево, включающее в себя каждую вершину, а также имеет минимальную сумму весов среди всех деревьев, которые могут быть сформированы из графа.
Он подпадает под класс алгоритмов, называемых «жадными» алгоритмами , которые находят локальный оптимум в надежде найти глобальный оптимум.
Мы начинаем с одной вершины и продолжаем добавлять ребра с наименьшим весом, пока не достигнем нашей цели.
Шаги для реализации алгоритма Прима следующие:
-
Инициализируйте минимальное остовное дерево с произвольно выбранной вершиной. -
Найдите все ребра, которые соединяют дерево с новыми вершинами, найдите минимум и добавьте его в дерево. -
Продолжайте повторять шаг 2, пока не получите минимальное остовное дерево.
-
Деревья с корнем. -
Произвольно зафиксируем некоторую вершину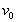 дерева
дерева 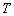 и назовем ее корнем дерева. Само дерево в этом случае будем называть деревом с корнем или корневым деревом.
и назовем ее корнем дерева. Само дерево в этом случае будем называть деревом с корнем или корневым деревом. -
Иногда полезно, руководствуясь какими–либо соображениями, выделять в дереве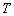 некоторую определенную цепь
некоторую определенную цепь 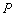 , которую обычно называют стволом дерева. Корень дерева обычно является одной из концевых вершин ствола. Каждая концевая вершина дерева
, которую обычно называют стволом дерева. Корень дерева обычно является одной из концевых вершин ствола. Каждая концевая вершина дерева 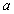 связана с ближайшей вершиной
связана с ближайшей вершиной 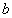 ствола единственной цепью. Эту цепь называют ветвью дерева, выходящей из вершины
ствола единственной цепью. Эту цепь называют ветвью дерева, выходящей из вершины 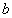 в вершину
в вершину 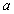 . При отсутствии у дерева ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева с его корнем.
. При отсутствии у дерева ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева с его корнем. -
Корневые деревья естественно ориентировать, если в этом есть необходимость, от корня. Все ребра, инцидентные корню дерева, считаются исходящими из корня и заходящими в вершины, смежные корню. Все ребра дерева, инцидентные вершинам, удаленным на расстояние 1 от корня, считаются исходящими из этих вершин и заходящими в вершины, им смежные. Процесс ориентации ребер продолжается подобным образом до тех пор, пока не будут ориентированы все ребра дерева. Поученное в результате такой ориентации дерево с корнем называется ориентированным деревом. В нем все ребра имеют направление от корня. Если поменять направления всех дуг ориентированного дерева на противоположные (к корню), то получившийся в итоге ориентированный граф называют сетью сборки.
6. Двоичные деревья. Двоичное дерево поиска.
Двоичным деревом поиска (ДДП) называют дерево, все вершины которого упорядочены, каждая вершина имеет не более двух потомков (назовём их левым и правым), и все вершины, кроме корня, имеют родителя. Вершины, не имеющие потомков, называются листами.
• Подразумевается, что каждой вершине соответствует элемент или несколько элементов, имеющие некие ключевые значения, в дальнейшем именуемые просто ключами.
• ДДП позволяет выполнять следующие основные операции:
▫ Поиск вершины по ключу.
▫ Определение вершин с минимальным и максимальным значением ключа.
▫ Переход к предыдущей или последующей вершине, в порядке, определяемом ключами.
▫ Вставка вершины.
▫ Удаление вершины.
Двоичное дерево может быть логически разбито на уровни. Корень дерева является нулевым уровнем, потомки корня – первым уровнем, их потомки – вторым, и т.д. Глубина дерева это его максимальный уровень.
• Каждую вершину дерева можно рассматривать как корень поддерева, которое определяется данной вершиной и всеми потомками этой вершины, как прямыми, так и косвенными. Поэтому о дереве можно говорить как о рекурсивной структуре.
-
Алгоритм Дейкстры нахождения кратчайших путей в нагруженном орграфе.
Алгоритм Дейкстры позволяет найти кратчайшие пути от данной вершины до всех остальных вершин в графе. Алгоритм состоит из следующих шагов:
-
Положить для всех вершин (кроме исходной) расстояние dist(v) = INF, для исходной dist(start) = 0 -
Выбрать непомеченную вершину v, с минимальным расстоянием. Если такой вершины нет, то завершить работу -
Пометить v
-
Для всех непомеченных вершин, смежных с v, попытаться улучшить оценку расстояния -
Вернуться к шагу 2
-
Эйлеровы графы. Условие существования Эйлеровых циклов.
Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то такой цикл называется эйлеровым циклом, а граф называется эйлеровым графом. Если граф имеет цепь (не обязательно простую), содержащую все ребра графа по одному разу, то такая цепь называется эйлеровой цепью, а граф называется полуэйлеровым графом.
Рассмотрим алгоритм построения эйлерова цикла в эйлеровом графе.
Алгоритм Флери.
Начиная с произвольной вершины, идем по ребрам графа, соблюдая следующие правила:
1. Удаляем ребра по мере их прохождения, и удаляем также изолированные вершины, которые при этом образуются.
2. Идем по мосту только тогда, когда нет других возможностей.
По теореме граф является эйлеровым. На диаграмме ребра пронумерованы в порядке их прохождения, таким образом эйлеров цикл abcdf edbeca.
-
Алгоритм построения Эйлерова цикла в графе.
Алгоритм нахождения эйлерова цикла.
-
Выбрать произвольную вершину А -
Выбрать произвольно некоторое ребро, инцидентное вершине А, и присвоить ему номер 1. Это ребро называется помеченным -
Каждое пройденное ребро вычеркиваем и присваиваем ему номер на 1 больше предыдущего пройденного ребра -
Находясь в вершине X, не выбираем ребра, соединяющие вершину X с вершиной А, если есть возможность другого выбора -
Находясь в вершине X, не выбираем рёбра, являющиеся мостом
-
После того как в графе пронумерованы все ребра, цикл образован ребрами с номерами от 1 до n, который является эйлеровым
-
Гамильтоновы графы.
Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Если граф имеет простую цепь, содержащую все вершины графа по одному разу, то такая цепь называется гамильтоновой цепью, а граф называется полугамильтоновым графом.
-
Задача коммивояжера и способы ее решения.
Задача коммивояжера — пожалуй, одна из самых известных оптимизационных задач. Ее цель заключается в нахождении самого выгодного маршрута (кратчайшего, самого быстрого, наиболее дешевого), проходящего через все заданные точки (пункты, города) по одному разу, с последующим возвратом в исходную точку. Условия задачи должны содержать критерий выгодности маршрута (т. е. должен ли он быть максимально коротким, быстрым, дешевым или все вместе), а также исходные данные в виде матрицы затрат (расстояния, стоимости, времени и т. д.) при перемещении между рассматриваемыми пунктами. Особенности задачи в том, что она довольно просто формулируется и найти хорошие решения для нее также относительно просто, но вместе с тем поиск действительно оптимального маршрута для большого набора данных — непростой и ресурсоемкий процесс. Для решения задачи коммивояжера ее надо представить как математическую модель. При этом исходные условия можно записать в формате матрицы — таблицы, где строкам соответствуют города отправления, столбцам — города прибытия, а в ячейках указываются расстояния (время, стоимость) между ними; или в виде графа — схемы, состоящей из вершин (точек, кружков), которые символизируют города, и соединяющих их ребер (линий), длина которых соответствует расстоянию между городами. Виды задачи коммивояжера по симметричности ребер графа: симметричная (англ. «Symmetric TSP») — все пары ребер, соединяющих одни и те же вершины, имеют одинаковую длину (т. е. граф, представляющий исходные данные задачи, является неориентированным). Иными словами, длина прямого пути от города A до города B и длина обратного пути от города B до города A, одинаковы. То же самое справедливо и в отношении остальных пар городов (A-C и C-A, B-C и C-D, и т. д.); асимметричная (англ. «Asymmetric TSP») — длина пар ребер соединяющих одни и те же города, может различаться (ориентированный граф). Для этого типа задачи коммивояжера прямой путь, например, из города A в город B может быть короче или длиннее обратного пути из города B в город A. Такое может быть не только в теории, но и в реальности — в случае дорог с односторонним движением. Кроме того, в общем случае поиска кратчайшего пути охватывающего набор пунктов, которые требуется посетить по одному разу, говорят об обобщенной задаче коммивояжера (англ. «Generalized TSP»). Типы задачи коммивояжера по замкнутости маршрута: замкнутая — нахождение кратчайшего пути, проходящего через все вершины по одному разу с последующим возвратом в точку старта (маршрут получается замкнутым, закольцованным); незамкнутая — нахождение кратчайшего пути, проходящего через все вершины по одному разу и без обязательного возврата в исходную точку (маршрут получается разомкнутым). Можно предложить и другие классификации задачи коммивояжера (например, метрическая и неметрическая), но в данном случае не стоит перегружать ими статью. В этой статье мы рассматриваем алгоритм решения именно для замкнутого варианта задачи (т. е. с возвратом в исходную точку). Методы решения задачи коммивояжера довольно разнообразны и различаются применяемым инструментарием, точностью находимого решения и сложностью требуемых вычислений. Вот лишь некоторые из них: полный перебор (метод «грубой силы», англ. «Brute Force») — заключается в последовательном рассмотрении всех возможных маршрутов и выборе из них оптимального. Метод самый простой и точный, но неэффективный и при большом количестве городов его применение становится затруднительным ввиду значительных затрат времени и ресурсов на перебор огромного количества вариантов решения задачи. Для ускорения и повышения эффективности полного перебора используются различные приемы: метод ветвей и границ, параллельные вычисления, радужные таблицы; случайный перебор — в этом случае вычисляются не все возможные варианты маршрута, а лишь некоторые выбранные в случайном порядке (например, с помощью генератора случайных чисел). Из рассмотренных вариантов затем выбирается наилучший. Конечно, вероятнее всего полученное решение не будет оптимальным (впрочем, оно не будет и самым худшим), но зато данный метод требует меньших затрат времени и вычислительных ресурсов, а потому в некоторых случаях его применение оправдано; динамическое программирование — ключевая идея заключается в вычислении и запоминании пройденного пути от исходного города до всех остальных, последующем прибавлении к нему расстояний от текущих городов до оставшихся, и так далее. По сравнению с полным перебором этот метод позволяет существенно сократить объем вычислений; жадные алгоритмы (англ. «Greedy») — основаны на нахождении локально оптимальных решений на каждом этапе вычислений и допущении, что найденное таким образом итоговое решение будет глобально оптимальным. Т. е. на каждой итерации выбирается лучший участок пути, который включается в итоговый маршрут. Метод простой, но его большой недостаток в том, что может возникнуть ситуация, когда окажется, что начальная и конечная точки маршрута разнесены далеко друг от друга и их придется соединять длинным отрезком пути, что значительно снизит эффективность решения. К жадным алгоритмам относятся: метод ближайшего соседа (англ. «Nearest Neighbour»), модифицированный метод ближайшего соседа (англ. «Double Ended Nearest Neighbour»), метод самого дешевого включения и т. д.; метод минимального остовного дерева — поиск маршрута ведется на графе. Для нахождения оптимального пути применяются различные инструменты: алгоритм Прима, алгоритм Краскала, алгоритм Борувки; метод имитации отжига — один из численных методов Монте-Карло; метод эластичной сети — каждый из возможных маршрутов рассматривается как отображение окружности на плоскость; муравьиный алгоритм — эвристический метод, основанный на моделировании поведения муравьев, ищущих пути от своей колонии к источникам пищи. Первую версию такого алгоритма предложил доктор наук Марко Дориго в 1992 году. Этот метод позволяет относительно быстро найти хорошее, но не обязательно оптимальное решение; генетический алгоритм — еще один эвристический метод, заключающийся в случайном подборе и комбинировании исходных параметров с использованием механизмов имитирующих естественный отбор в процессе эволюции (наследование, мутации, кроссинговер). Несмотря на довольно широкие возможности применения (и не только в логистике), этот метод часто становится объектом критики; метод ветвей и границ — один из методов дискретной оптимизации, являющийся развитием метода полного перебора, но отличающийся от него отсевом в процессе вычисления подмножеств неэффективных решений.
-
Алгебра логики.
Алгеброй логики называется аппарат, который позволяет выполнять действия над высказываниями.
Алгебру логику называют также алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля, разработавшего в XIX веке ее основные положения. В булевой алгебре высказывания принято обозначать прописными латинскими буквами: A, B, X, Y. В алгебре Буля введены три основные логические операции с высказываниями: Сложение, умножение, отрицание. Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.
Логические выражения могут быть простыми и сложными.
Простое логическое выражение состоит из одного высказывания и не содержит логические операции. В простом логическом выражении возможно только два результата — либо «истина», либо «ложь».
Сложное логическое выражение содержит высказывания, объединенные логическими операциями. По аналогии с понятием функции в алгебре сложное логическое выражение содержит аргументы, которыми являются высказывания.
В качестве основных логических операций в сложных логических выражениях используются следующие:
• НЕ (логическое отрицание, инверсия);
• ИЛИ (логическое сложение, дизъюнкция);
• И (логическое умножение, конъюнкция).
Логическое отрицание является одноместной операцией, так как в ней участвует одно высказывание. Логическое сложение и умножение — двуместные операции, в них участвует два высказывания. Существуют и другие операции, например операции следования и эквивалентности, правило работы которых можно вывести на основании основных операций.
Все операции алгебры логики определяются таблицами истинности значений. Таблица истинности определяет результат выполнения операции для всех возможных логических значений исходных высказываний. Количество вариантов, отражающих результат применения операций, будет зависеть от количества высказываний в логическом выражении, например:
-
таблица истинности одноместной логической операции состоит из двух строк: два различных значения аргумента — «истина» (1) и «ложь» (0) и два соответствующих им значения функции; -
в таблице истинности двуместной логической операции — четыре строки: 4 различных сочетания значений аргументов — 00, 01, 10 и 11 и 4 соответствующих им значения функции; -
если число высказываний в логическом выражении N, то таблица истинности будет содержать 2N строк, так как существует 2N различных комбинаций возможных значений аргументов.
-
Способы задания логических функций.
Определение. Функция f(x0, x1, …, xn) называется логической (булевой), если ее аргументы x0, x1, …, xn и значения функции могут принимать только два значения: логического 0 и логической 1.
Для задания функции алгебры логики, как и любой другой функции необходимо поставить в соответствие значения функции для всех возможных комбинаций входных аргументов. Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n.
Способы задания логических функций
1. Словесный. Взаимосвязь значений функции и ее аргументов описывается словесной формулировкой.
2. Табличный. При табличном способе строится таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов. В отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов.
3. Цифровой. Функцию алгебры логики определяют в виде последовательности десятичных чисел. При этом последовательно расписывают эквиваленты двоичных кодов, которые соответствуют единичным либо нулевым значениям функции.
4. Аналитический. Функция алгебры логики записывается в виде аналитического выражения, где показаны логические операции, выполняемые над аргументами функции.
13.Существенные и фиктивные переменные логических функций.
Определение 1. Функция f(x1, x2, … xi-1, xi, xi+1, … xn) существенно зависит от переменной xi, если у переменных x1, …, xi-1, xi+1, …xn существует такой набор значений α1, …, αi-1, αi+1, …αn, что выполняется неравенство: f(α1, α2, … αi-1, 0, αi+1, … αn) ≠ f(α1, α2, … αi-1, 1, αi+1, … αn). В этом случае переменную xi называют существенной. Если же xi не является существенной, то ее называют фиктивной.
Определение 2. Переменную xi называют фиктивной, если для любого набора значений α1, …, αi-1, αi+1, …αn переменных x1, …, xi-1, xi+1, …xn выполняется равенство: f(α1, α2, … αi-1, 0, αi+1, … αn) = f(α1, α2, … αi-1, 1, αi+1, … αn).
-
Логические функции одной и двух переменных.
Логической функцией называют функцию F (Х1, Х2, ..., Х n), аргументы которой Х 1, Х 2, ..., Х n и сама функция принимают значения 0 или 1. Таблицу, показывающую, какие значения принимает логическая функция при всех сочетаниях значений ее аргументов, называют таблицей истинности логической функции.
-
Суперпозиция логических функций.
это функция, полученная из некоторого множества функций путем подстановки одной функции в другую или отождествления переменных. Множество всех возможных не эквивалентных друг другу суперпозиций данного множества функций образует замыкание данного множества функций.
-
Законы алгебры логики.
1. Закон тождества
Х = Х
Всякое высказывание тождественно самому себе.
2. Закон исключенного третьего
X \/ ¬X = 1
Высказывание может быть либо истинным, либо ложным, третьего не дано. Следовательно, результат логического сложения высказывания и его отрицания всегда принимает значение «истина».
3. Закон непротиворечия
X/\ ¬X = 0
Высказывание не может быть одновременно истинным и ложным. Если высказывание Х истинно, то его отрицание НЕ Х должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно.
4. Закон двойного отрицания
¬¬X = X
Если дважды отрицать некоторое высказывание, то в результате получим исходное высказывание.
5. Переместительный (коммутативный) закон
X /\ Y = Y /\ X
X /\ Y = YX
Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.
6. Сочетательный (ассоциативный) закон
(X \/Y) \/Z = X \/ (Y \/Z)
(X/\Y)/\Z=X/\(Y/\Z)
При одинаковых знаках скобки можно ставить произвольно или вообще опускать.
5. Распределительный (дистрибутивный) закон
(X /\ Y) \/ Z= (X /\ Z) \/ (Y /\ Z)
(X /\ Y) \/ Z = (X \/ Z) /\ (Y \/ Z)
Определяет правило выноса общего высказывания за скобку.
7. Закон общей инверсии Закон де Моргана
¬(X \/ Y) = ¬X /\ ¬Y
¬(X /\ Y) = ¬X \/ ¬Y
Закон общей инверсии.
8. Закон равносильности (идемпотентности)
A\/A= A;
A/\ A = A.
от латинских слов idem — тот же самый и potens —сильный
9. Законы исключения констант:
A\/ 1 = 1, A\/ 0 = A;
A/\1 = A, A/\0 = 0.
10. Закон поглощения:
A\/ (A/\B) = A;
A/\ (A\/B) = A.
11. Закон исключения (склеивания):
(A/\B) \/ (¬A/\B) = B;
(A\/B)/\(¬A \/B) = B.
12. Закон контрапозиции
(правило перевертывания):
(A<=>B) = (B<=>A).
13. А => В = ¬A \/ В;
14. ¬ (A=>B)=A/\B
15. А <=>В = (А /\ В) \/ (¬A /\ ¬B);
16. А <=>В = (¬A \/ В) /\ (А \/¬B).
17.Функционально полные системы логических функций.
Функционально полная система логических элементов - это такой набор элементов, используя который можно реализовать любую сколь угодно сложную логическую функцию. Поскольку любая логическая функция представляет собой комбинацию простейших функций - дизъюнкции, конъюнкции и инверсии, то набор из элементов трех типов, реализующих соответственно функции И, или и НЕ, естественно, является функционально полным.
18. Дизъюнктивная нормальная форма (ДНФ).
Дизъюнкти́вная норма́льная фо́рма (ДНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов. Любая булева формула может быть приведена к ДНФ. Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности.
19. Совершенная дизъюнктивная нормальная форма (СДНФ).
одна из форм представления функции алгебры логики (булевой функции) в виде логического выражения. Представляет собой частный случай ДНФ, удовлетворяющий следующим трём условиям:
-
в ней нет одинаковых слагаемых (элементарных конъюнкций); -
в каждом слагаемом нет повторяющихся переменных; -
каждое слагаемое содержит все переменные, от которых зависит булева функция (каждая переменная может входить в слагаемое либо в прямой, либо в инверсной форме).
Любая булева формула, не являющаяся тождественно ложной, может быть приведена к СДНФ, причём единственным образом, то есть для любой выполнимой функции алгебры логики существует своя СДНФ, причём единственная.
20. Конъюнктивная нормальная форма (КНФ).
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ. Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.
21. Совершенная конъюнктивная нормальная форма (СКНФ).
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
1.в ней нет одинаковых элементарных дизъюнкций
2.в каждой дизъюнкции нет одинаковых пропозициональных переменных
3.каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв
22. Сведение логических формул к ДНФ.
Шаг 1. Все подформулы A вида B C (т.е. содержащие импликацию) заменяем на BVC или на (B&C).
Шаг 2. Все подформулы A вида B
Приведение ДНФ к СДНФ.
Шаг 1. Используя алгоритм построения ДНФ, находим формулу В, являющуюся ДНФ формулы А.
Шаг 2. Вычеркиваем в B все элементарные конъюнкции, в которые одновременно входят какая-нибудь переменная и ее отрицание. Это обосновывается равносильностями:
A&A 0, B&0 0, СV0 С.
Шаг 3. Если в элементарной конъюнкции формулы B некоторая переменная или ее отрицание встречается несколько раз, то оставляем только одно ее вхождение. Это обосновывается законом идемпотентности для конъюнкции: A&A A.
Шаг 4. Если в элементарную конъюнкцию С формулы В не входит ни переменная x, ни ее отрицание x, то на основании 1- го закона расщепления заменяем С на (С&x) V (C&x).
Шаг 5. В каждой элементарной конъюнкции формулы B переставляем конъюнктивные члены так, чтобы для каждого i (i = 1, ..., n) на i-м месте была либо переменная xi, либо ее отрицание xi.
Шаг 6. Устраняем возможные повторения конъюнктивных членов согласно закону идемпотентности для дизъюнкции: СVС С.
24. Приведение ДНФ к КНФ
Шаг 1. Все подформулы A вида B C (т.е. содержащие импликацию) заменяем на BVC или на (B&C).
Шаг 2. Все подформулы A вида B C (т.е. содержащие эквивалентность) заменяем на (A&B) V (A&B) или на (AVB)&(AVB).
Шаг 3. Все отрицания, стоящие над сложными подформулами, опускаем по законам де Моргана.
Шаг 4. Устраняем все двойные отрицания над формулами (в соответствии с равносильностью 8).
Шаг 5. Осуществляем раскрытие всех скобок по закону дистрибутивности дизъюнкции относительно конъюнкции для КНФ.
-
Двойственные логические функции.
Определение. Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть
f*(x1, …, xn) =f (x 1, …, x n).
-
Принцип двойственности.
Двойственность, или принцип двойственности, — принцип, по которому задачи оптимизации можно рассматривать с двух точек зрения, как прямую задачу или двойственную задачу. Решение двойственной задачи даёт нижнюю границу прямой задачи (при минимизации). Однако, в общем случае, значения целевых функций оптимальных решений прямой и двойственной задач не обязательно совпадают.
-
Полиномиальные алгоритмы и труднорешаемые задачи. NP-полные задачи.
Алгоритм называется полиномиальным (или имеющим полиномиальную временную сложность), если его временная сложность f(n) равна: O(p(n)) для некоторого полинома p(n). Задача называется труднорешаемой, если для ее решения не существует полиномиального алгоритма.
Попытки найти алгоритмы полиномиальной сложности для решения некоторых задач привели к понятию недетерминированной машины Тьюринга для (НДМТ) распознавания свойств, полученной из обычной машины Тьюринга заменой конечного состояния q0 на два заключительных состояния – qY и qN . Машина проверяет, удовлетворяют ли входные данные заданному свойству. Если она заканчивает работу в состоянии qY , то получен ответ «да», если заканчивает в состоянии qN , то получен ответ «нет». Недетерминированная машина Тьюринга, помимо головки чтения/записи имеет дополнительное устройство, которое называется угадывающем модулем. Этот модуль может только записывать на ленту. Угадывающий модуль дает информацию для записи «догадки».
Программа для НДМТ (НДМТ-программа) определяется как и для машины Тьюринга в виде частичной функции p: Q x A ® Q x A x {L,S,R}. Вычисление на НДМТ в отличии от вычисления на машине Тьюринга имеет две различные стадии.
На первой стадии происходит «угадывание». В начальный момент времени входное слово w записывается в ячейках с номерами 1, 2, …, |w|, головка чтения/записи смотрит на ячейку 0, пишущая головка угадывающего модуля смотрит на ячейку с номером –1. Угадывающий модуль начинает управлять угадывающей головкой, которая делает один шаг в каждый момент времени и либо пишет в находящейся под ней ячейке одну из букв алфавита A и сдвигается влево, либо останавливается. В последнем случае угадывающий модуль заканчивает работу и начинает работать программа p.
Начиная с этого момента, вычисление НДМТ-программы осуществляется по тем же правилам, что и вычисление на машине Тьюринга. Вычисление заканчивается тогда, когда управляющее устройство перейдет в одно из заключительных состояний (qY и qN); оно называется принимающим вычислением, если остановка происходит в состоянии qY . Остальные вычисления, в том числе не заканчивающиеся, называются непринимающими.
Любая НДМТ-программа p может иметь бесконечное число возможных вычислений при данном входе w, по одному для каждого слова-догадки из A*. Будем говорить, что НДМТ-программа p принимает w, если по крайней мере одно из ее вычислений, имеющих w на входе, является принимающим. Язык,
распознаваемый программой p, - это язык Lp = {w Î A* : p принимает w}. Временем, требующимся НДМТ-программе p для того, чтобы принять слово w Î Lp , называется минимальное число шагов, выполняемых на стадии угадывания и проверки до момента достижения заключительного состояния qY , где минимум берется по всем принимающим вычислениям программы p на входе w. Временной сложностью НДМТ-программы p называется функция Tp : N+® N+, где N+ = {1, 2, 3, …}, определенная как Tp (n) = max {{1}È{m: существует w Î Lp , |w| = n, такое что время принятия w программой p равно m}}.
Если существует такой полином p(n) , что Tp (n) £ p(n) для всех n ³ 1, то НДМТ-программа называется имеющей полиномиальное время работы.
Класс NP – это класс (не обязательно всех) задач распознавания свойств (т.е. задач, решениями которых могут быть либо «да», либо «нет»), которые могут быть решены с помощью НДМТ-программы с полиномиальным временем работы. Большинство практически важных задач, для которых в настоящее время не известны полиномиальные алгоритмы, после переформулировки их в виде задач распознавания свойств, попадают в этот класс.
Задача из NP называется NP-полной, если всякая другая задача из класса NP может быть сведена к ней за полиномиальное время. Таким образом, если для некоторой NP-полной задачи существует полиномиальный алгоритм, то и любая задача из класса NP полиномиальна разрешима, а если какая-то задача из NP труднорешаемая, то и любая NP-полная задача является труднорешаемой.
-
Анализ трудоемкости алгоритмов задач комбинаторики и задач теории графов.
Целью анализа трудоёмкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.
Трудоёмкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоёмкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.
Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных. Используемая в асимптотическом анализе оценка функции трудоёмкости, называемая сложностью алгоритма, позволяет определить, как быстро растет трудоёмкость алгоритма с увеличением объема данных. В асимптотическом анализе алгоритмов используются обозначения, принятые в математическом асимптотическом анализе. Ниже перечислены основные оценки сложности.