ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ

Задача3.ПроцесспроизводстваописываетсяспомощьюфункциивыпускаQ(K,L)= 4K^1/3L^2/3.Определите,насколькопроцентовуменьшатсязатратыкапиталаК,еслизатратытрудаLувеличатсяна25%(уровеньвыпускапри этомсохраняется). 1 2^{Задача 14. Функция полезности имеет вид: U(x}1^,x2^{) = x 0,6x 0,25. Известны цены натоварыр}1^{=8у.д.е.,р}2^{=5у.д.е.ибюджетI=680у.д.е.А)Найдитеоптимальныйпотре-}бительский набор и соответствующее значение функции полезности. Б) На сколько вырастет полезность потребительского набора, если бюджет вырастет на 1 д.е.? Задача21.ДаныфункцииспросаипредложениянанекоторыйтоварQ_D150P^,Q_S 50  3P . А) Найдите параметры равновесия. Б) На единицу продаваемого то-вара был введен налог, в результате чего новая равновесная цена составила 60 ден.ед.Определитеразмерналогаиновыйобъемпродаж.Задача 40. Издательство решает вопрос об издании новой книги известного писа-^{теля, спрос на которую оценивается функцией Q}D ^{= 80 - 0,4р (тыс. шт), где р – цена,}руб. Постоянные издержки составляют 1200 тыс. руб. Себестоимость 1 экземпляракниги 40 рублей. При этом за право издания оно должно выплатить писателю гоно-рар600тыс.руб.Возьметсялииздательствоиздаватькнигу,еслионоприменит«по-литику снятия сливок», установив изначально высокую цену, по которой книгу, пооценкам экспертов, купит 3/4 читателей,

---

готовых это сделать по такой цене, а затем снизив цену?

Задача 49. Дана матрица А коэффициентов прямых материальных затрат с компо- ^{нентами ( aij) и вектор конечного выпуска У с компонентами (у}i⁾



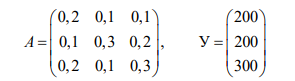
А) постройте модель (таблицу) межотраслевого баланса

Б) найдите объем валового выпуска каждого вида продукции, если конечный выпуск по первой и второй отраслям увеличить в 2 раза, а по третьей отрасли оставить без изменений.
Задача 56. Портфель состоит из активов двух компаний Micro и Macro, цены на акции которых на конец дня за некоторый период представлены в таблице

дата	цена-Micro	цена-Macro
20211001	13,5	70
20211002	13,588	70,74
20211003	13,5	71,3
20211004	13,468	72,2
20211005	13,47	72,81
20211006	13,454	72,83
20211007	13,526	72,83
20211008	13,524	74,56
20211009	13,49	75,6
20211010	13,484	73,4
20211011	13,5	74,56
20211012	13,542	77,3
20211013	13,4	77,36
20211014	13,35	77,36
20211015	13,344	76,76

---

1. 
   Рассчитайте значения доходностей акций компаний Micro и Macro.
   
2. 
   Вычислите средние ожидаемые значения доходностей и риски вложений в акции компаний Micro и Macro, а также коэффициент корреляции доходностей этих ком- паний.
   
3. 
   ^{Найдите портфель Х*(х}1^{, х}2^{) максимальной доходности, риск которого не превос- ходит }0^=0,006.
   
4. 
   Визуализируйте найденный портфель в виде круговой диаграммы.
   
5. 
   В ответе выпишите оптимальный портфель и его доходность.
   

---

Смотрите также файлы

• Бизнес план парикмахерской.pdf

• Бу хмаоюгры кондинская районная больница.docx

• В настоящее время все организации независимо от их вида, форм собственности и подчинённости ведут бухгалтерский учёт имущества и хозяйственных операций согласно действующему законодательству.docx

• Выявление опасностей, опасных ситуаций.doc

• История средневековья от Падения Рима 476 до Взятия Константинополя 1453.docx