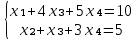Файл: Решение Методом Крамера Воспользуемся формулой для вычисления определителя матрицы 33.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 10
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
АНО ПО «Открытый социально-экономический колледж»
Программа среднего профессионального образования
40.02.01. Право и организация социального обеспечения СОО
Дисциплина: математика
Практическое задание № 2
Выполнил:
слушатель Астахова Мария Владимировна
Преподаватель: Васильцова Анна Сергеевна
Тула 2023 г.
Задание №1. Решить систему линейных уравнений методом Гаусса и методом Крамера:
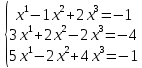
Решение:
Методом Крамера:
Воспользуемся формулой для вычисления определителя матрицы 3×3:
∆ =
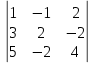
∆ =
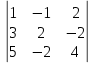 = 1·2·4 + (-1)·(-2)·5 + 2·3·(-2) - 2·2·5 - 1·(-2)·(-2) - (-1)·3·4 = 8 + 10 - 12 - 20 - 4 + 12 = -6
= 1·2·4 + (-1)·(-2)·5 + 2·3·(-2) - 2·2·5 - 1·(-2)·(-2) - (-1)·3·4 = 8 + 10 - 12 - 20 - 4 + 12 = -6∆1 =
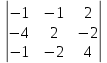
∆1 =
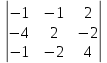 =(-1)·2·4 + (-1)·(-2)·(-1) + 2·(-4)·(-2) - 2·2·(-1) - (-1)·(-2)·(-2) - (-1)·(-4)·4 = -8 - 2 + 16 + 4 + 4 - 16 = -2
=(-1)·2·4 + (-1)·(-2)·(-1) + 2·(-4)·(-2) - 2·2·(-1) - (-1)·(-2)·(-2) - (-1)·(-4)·4 = -8 - 2 + 16 + 4 + 4 - 16 = -2∆2=
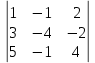
∆2=
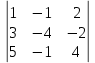 =1·(-4)·4 + (-1)·(-2)·5 + 2·3·(-1) - 2·(-4)·5 - 1·(-2)·(-1) - (-1)·3·4 = -16 + 10 - 6 + 40 - 2 + 12 = 38
=1·(-4)·4 + (-1)·(-2)·5 + 2·3·(-1) - 2·(-4)·5 - 1·(-2)·(-1) - (-1)·3·4 = -16 + 10 - 6 + 40 - 2 + 12 = 38∆3=
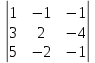
∆3=
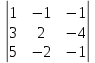 =1·2·(-1) + (-1)·(-4)·5 + (-1)·3·(-2) - (-1)·2·5 - 1·(-4)·(-2) - (-1)·3·(-1) = -2 + 20 + 6 + 10 - 8 - 3 =
=1·2·(-1) + (-1)·(-4)·5 + (-1)·3·(-2) - (-1)·2·5 - 1·(-4)·(-2) - (-1)·3·(-1) = -2 + 20 + 6 + 10 - 8 - 3 =
23
Х1=
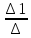 =
=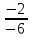 =
=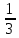
Х2=
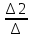 =
=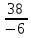 =
=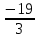 =-6
=-6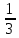
Х3=
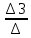 =
=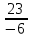 =-
=- 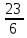 =-3
=-3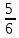
Методом Гаусса:
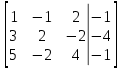
от 2 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 5:
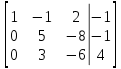
2-ую строку делим на 5:
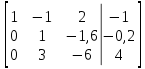
к 1 строке добавляем 2 строку, умноженную на 1; от 3 строки отнимаем 2 строку, умноженную на 3:
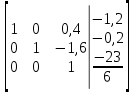
от 1 строки отнимаем 3 строку, умноженную на 0.4; к 2 строке добавляем 3 строку, умноженную на 1.6:
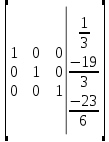
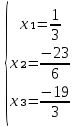
Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления:
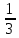 —
— 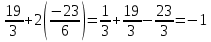
3
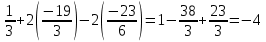
5
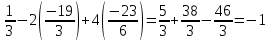
Проверка выполнена успешно.
Ответ:
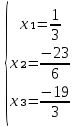
Задание №2. Решить систему линейных уравнений.
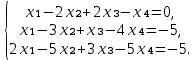
Решение:
Из 1-ого уравнения выразим x₁ через остальные переменные:
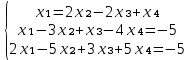
Во 2, 3 уравнение подставляем х₁ :
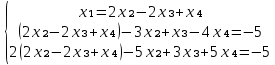
После упрощения получим:
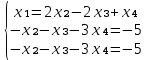
Поделим 2-ое уравнение на -1
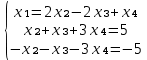
Из 2-ого уравнения выразим x2 через остальные переменные
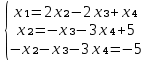
В 3 уравнение подставляем x₂
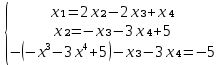
после упрощения получим:
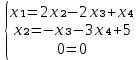
Ответ: