МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИФедеральное государственное бюджетное образовательное учреждениевысшего образования«Сибирский государственный университет науки и технологий имени академика М.Ф. Решетнева»АЭРОКОСМИЧЕСКИЙ КОЛЛЕДЖОбеспечение информационной безопасности автоматизированных систем10.02.05ОТЧЕТ О ПРАКТИЧЕСКОМ ЗАНЯТИИ № 9КРИПТОАНАЛИЗ ШИФРА ШИФРА ВИЖИНЕРА. Преподаватель ___________ Черников А.К.подпись, дата инициалы, фамилияОбучающийся БИАССК 5-21 ____________ Дмитриев И.Сномер группы, зачетной книжки подпись, дата инициалы, фамилияКрасноярск 2022ОТЧЁТ ПО ПРАКТИЧЕСКОМУ ЗАНЯТИЮ № 9Тема: Криптоанализ шифра Вижинера.Цель: Научиться расшифровывать и анализировать сообщения, зашифрованные шифром Виженера.Ход работыВариант- 3Текст номер-3

1. 
   Запустил ПО Cryptool. Создадим новый проект в меню File ->New.
   

Рисунок 1– ПО Cryptool

2. 
   Получаем график частности полученный при криптоанализе
   

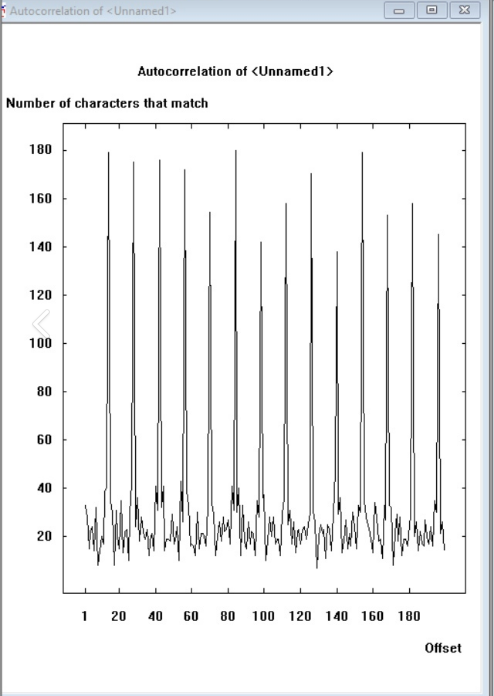
Рисунок 2- График

3. 
   Получаем полученный текст
   

Рисунок 3- ТекстКонтрольные Вопросы

1. 
   Криптографическая стойкость (или криптостойкость) — способность криптографического алгоритма противостоять криптоанализу. Стойким считается алгоритм, успешная атака на который требует от атакующего обладания недостижимым на практике объёмом вычислительных ресурсов или перехваченных открытых и зашифрованных сообщений либо настолько значительных затрат времени на раскрытие, что к его моменту защищённая информация утратит свою актуальность.
   
2. 
   Big O notation - это математическая запись, которая может быть применена к алгоритмам, которые мы используем при разработке программного обеспечения. В этом контексте его целью является описание вычислительной сложности алгоритма. В частности, он позволяет оценить, насколько масштабируемым будет алгоритм по мере роста объема обрабатываемых данных.
   
3. 
   4. f(n) = O(1) константа
   f(n) = O(log(n)) логарифмический рост
   f(n) = O(n) линейный рост
   f(n) = O(n*log(n)) квазилинейный рост
   f(n) = O(n^m) полиномиальный рост
   f(n) = O(2^n) экспоненциальный рост
   
4. 
   Константная - O(1); Линейная - O(n); Логарифмическая - O(log n); Квадратичная - O(n2), O(n^2).
   

---

Вывод: Научился расшифровывать и анализировать сообщения, зашифрованные шифром Виженера.

---

Смотрите также файлы

• Рабочая программа по дисциплине инженерная графика Целью изучения дисциплины Инженерная графика.doc

• Вопросы на русском языке Укажите искусственный путь передачи вби.docx

• 1. Чем структура человеческого сознания отличается от структуры сознания животного.docx

• Задача 3 (.doc

• Проективные тесты.docx