ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Метод деления отрезка попала
clc
clf(1)
function y=f(x)
y=0.25*8*x.^3-2*x.^2+2.3*x-12
endfunction
x=-3:.1:5;
plot(x,f)
xgrid(1)
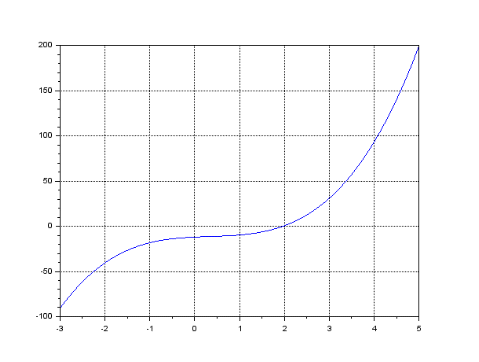
Из графика видно, что выражение имеет решение
Корень определен на отрезке от 2 до 3
| № | a | x=(a+b)/2 | b | f(a) | f(x) | f(b) | e=(b-a)/2 |
| 1 | 1 | 2 | 3 | -9,7 | 0,6 | 30,9 | 1 |
| 2 | 1 | 1,5 | 2 | -9,7 | -6,3 | 0,6 | 0,5 |
| 3 | 1,5 | 1,75 | 2 | -6,3 | -3,381 | 0,6 | 0,25 |
| 4 | 1,5 | 1,625 | 1,75 | -6,3 | -4,962 | -3,381 | 0,125 |
Ответ: 1,625±0,125
Метод Касательных
Определим знак производной функции
clc
function y=f1(x)
y=6*x.^2-4*x+2.3;
endfunction
x=1:.01:3;
plot(x,f1, 'g',"linewidth",3);
xgrid()
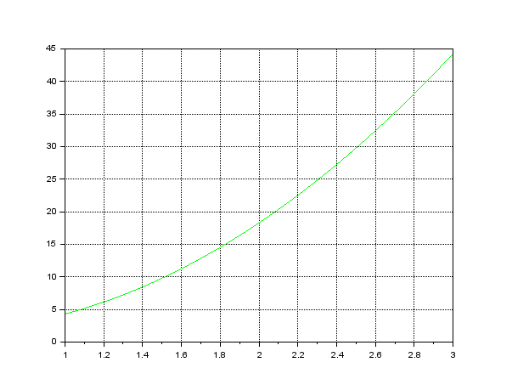
Y’’ очевидно имеет положительное значение
Пусть x0 будет b, т.к выполняется следующее условие :
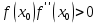
X0=3
Y(3)=30,9
Y’(3)=20,3
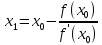
Первый отрезок
X1= 3 - 30,9/44,3= 2,302483
|x1-x0|=|2,302483-3|=0,69752
– ответ больше погрешности 0,1, поэтому нельзя считать корнем уравнения
Второй отрезок
X2= 2,302483 - 7,1058/24,899= 2,017096
|x2-x1|=|2,017096-2,302483|=0,28539
Третий отрезок
X3= 2,017096 - 0,9158/18,644=1,967975
|x3-x2|=|1,967975-2,017096|=0,04912
Ответ 1,967975+-0,04912
Решение в SCILAB
clc
function y=f(x)
y=2*x.^3-2*x.^2+2.3*x-12;
endfunction
[x,y]=fsolve(2,f)
x =
1.9666079
y =
-3.553D-15
Решение в EXEL
| x | y |
| 1,96661 | 3,19E-05 |
Ответ : 1,96661
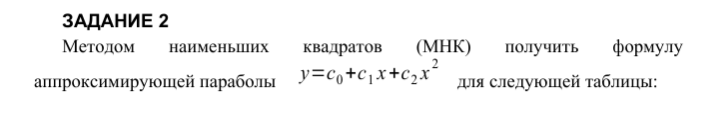
| x | 3 | 5 | 7 | 9 | 11 |
| y | 5,5 | 7,9 | 11 | 15,1 | 19,9 |
| | | | | | |
| x | y | x^2 | x^3 | x^4 | xy | yx^2 |
| 3 | 5,5 | 9 | 27 | 81 | 16,5 | 49,5 |
| 5 | 7,9 | 25 | 125 | 625 | 39,5 | 197,5 |
| 7 | 11 | 49 | 343 | 2401 | 77 | 539 |
| 9 | 15,1 | 81 | 729 | 6561 | 135,9 | 1223,1 |
| 11 | 19,9 | 121 | 1331 | 14641 | 218,9 | 2407,9 |
| 35 | 59,4 | 285 | 2555 | 24309 | 487,8 | 4417 |
59,4=5c0+35c1=285c2
487,8=35c0+285c1+2555c2
24309=285c0+2555c1+24309c2
a=[5 35 285;35 285 2555; 285 2555 24309]
b=[59.4 487.8 4417]
c=b/a'
c=
3.5264286 0.35 0.1035714
| x | y | Y=3.5264286 + 0.35x + 0.1035714x^2 | (y-Y)^2 |
| 3 | 5,5 | 5,5085712 | 7,35E-05 |
| 5 | 7,9 | 7,8657136 | 0,001176 |
| 7 | 11 | 11,0514272 | 0,002645 |
| 9 | 15,1 | 15,065712 | 0,001176 |
| 11 | 19,9 | 19,908568 | 0,005069 |
Ответ:
Уравнение аппроксимирующей параболы
Y=3.5264286 + 0.35x + 0.1035714x^2
Решение в EXEL
| x | y |
| 3 | 5,5 |
| 5 | 7,9 |
| 7 | 11 |
| 9 | 15,1 |
| 11 | 19,9 |
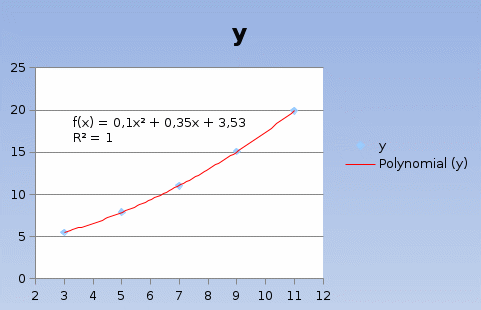
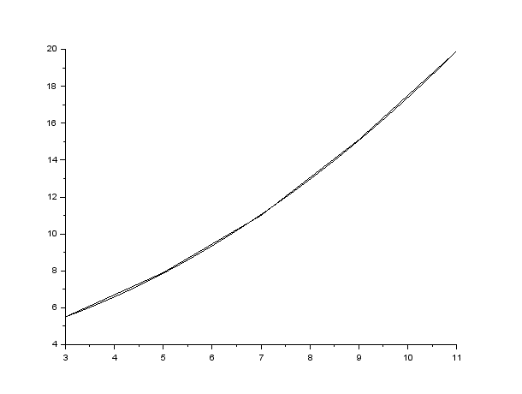
Решение в SCILAB
function y=G(c, z)
y=z(2)-c(1)-c(2)*z(1)-c(3)*z(1)^2
endfunction
x=[3 5 7 9 11];
y=[5.5 7.9 11 15.1 19.9];
z=[x;y];
c=[1;1;1];
a=datafit(G,z,c);
plot2d(x,y);
t=min(x):0.01:max(x);
Ptc=a(1)+a(2)*t+a(3)*t.^2;
plot2d(t,Ptc);
err=sum((y-a(1)-a(2)*x-a(3)*x.^2)^2)
printf("Сумма площадей квадратов отклонений равнa",err);
printf("Коэффициенты полинома")
disp(a)
err =
3.5264009
0.3500095
0.1035707

| x | 3 | 5 | 7 | 9 | 11 |
| y | 5,5 | 7,9 | 11 | 15,1 | 19,9 |
X*=3+12/30=3,4
А)
Решение в EXEL
| x | 3 | 5 | 7 |
| y | 5,5 | 7,9 | 11 |
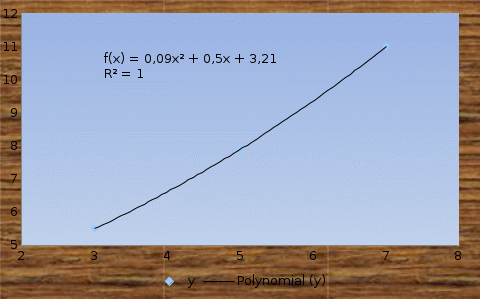
Уравнение ИЛП вычисляется по формуле Лагранжа
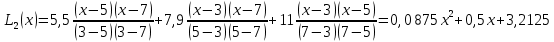
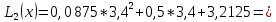 5,924
5,924 Решение в SCILAB
clc
clf()
x=[3 5 7];
y=[5.5 7.9 11];
nst=12;
n=length(x);
a=[];
b=[];
c=[];
for i=1:n
for j=1:n
a(i,j)=sum(x.^(i+j-2));
end
b(i)=sum(x.^(i-1).*y);
end
c=inv(a)*b
function z=f(t)
z=0;
for i=1:n
z=z+t.^(i-1).*c(i);
end
endfunction
plot2d(x,y,-4)
t=min(x)-.1:.01:max(x)+1;
plot2d(t,f(t))
r=min(x)+nst/30,z1=f(r), plot(r,z1,"*")
err=sum((y-f(x)).^2
printf("значение полинома в точке", r)
printf("равно",z1)
printf("сумма площадей квадратов отклонений равна", err)
printf("коффициенты полинома в порядке возрастания")
disp(c)
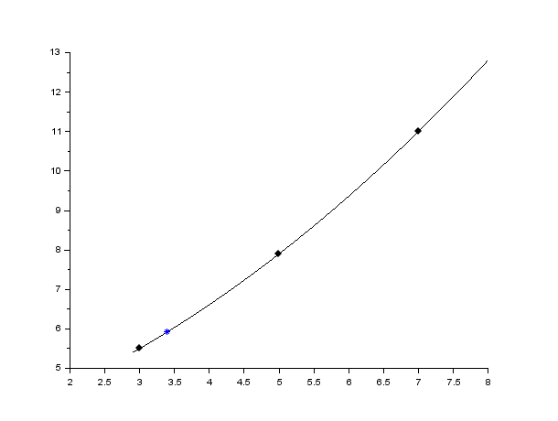
Значение полинома в точке 3.4 равно 5.9240000
коэффициенты полинома:
3.2125
0.5
0.0875
Ответ
Y=0,0875*3,4^2+0,5*3,4+5,2125
Y(3.4) = 5.9240000
Б)
Решение в EXEL
| x | y | Δy | Δ^2*y | Δ^3*y | Δ^4*y |
| 3 | 5,5 | 2,4 | 0,7 | 0,3 | -0,6 |
| 5 | 7,9 | 3,1 | 1 | -0,3 | |
| 7 | 11 | 4,1 | 0,7 | | |
| 9 | 15,1 | 4,8 | | | |
| 11 | 19,9 | | | | |
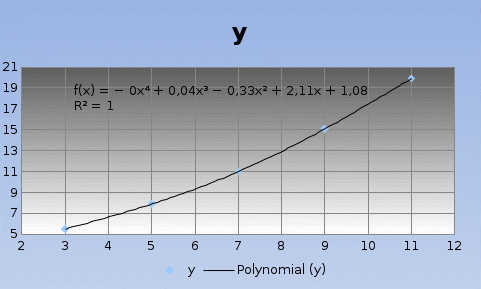
Уравнение интерполяционного полинома
y = -0,001x4 + 0,043x3 - 0,328x2 + 2,106x + 1,079
Решение в SCILAB
clc
clf()
x=[3 5 7 9 11];
y=[5.5 7.9 11 15.1 19.9];
nst=12;
n=length(x);
a=[];
b=[];
c=[];
for i=1:n
for j=1:n
a(i,j)=sum(x.^(i+j-2));
end
b(i)=sum(x.^(i-1).*y);
end
c=inv(a)*b
function z=f(t)
z=0;
for i=1:n
z=z+t.^(i-1).*c(i);
end
endfunction
plot2d(x,y,-4)
t=min(x)-.1:.01:max(x)+1;
plot2d(t,f(t))
r=min(x)+nst/30,z1=f(r), plot(r,z1,"*")
err=sum((y-f(x)).^2
printf("значение полинома в точке", r)
printf("равно",z1)
printf("сумма площадей квадратов отклонений равна", err)
printf("коффициенты полинома в порядке возрастания")
disp(c)
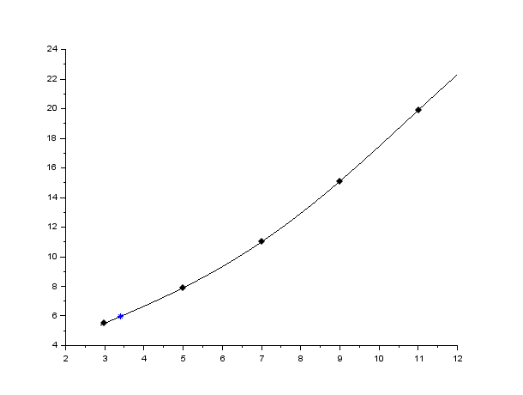
значение полинома в точке 3,4 равно 5.9585600
сумма площадей квадратов отклонений 0.00000
коэффициенты полинома
1.0796875
2.10625
-0.328125
0.04375
-0.0015625
Ответ:
Уравнение интерполяционного полинома
Y=1.0796875 + 2.10625x - 0.328125x^2 + 0.04375x^3 - 0.001562x^4

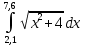
Решение в EXEL
| x | 2,1 | 2,65 | 3,2 | 3,75 | 4,3 | 4,85 | 5,4 | 5,95 | 6,5 | 7,05 | 7,6 |
| y=sqrt(x^2+4) | 2,900 | 3,320 | 3,774 | 4,250 | 4,742 | 5,246 | 5,758 | 6,277 | 6,801 | 7,328 | 7,859 |
Формула левых прямоугольников:
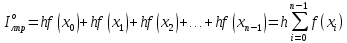
Формула правых треугольников
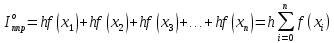
Формула трапеций