Введение в анализ

1. 
   
   Что называется функцией?
   
2. 
   Что называется областью определения и множеством значений функции.
   
3. 
   
   Какая функция называется монотонной; строго монотонной?
   
4. 
   Дайте определение четной (нечетной) функции.
   
5. 
   
   Что такое периодическая функция, период?
   
6. 
   Перечислите основные элементарные функции.
   
7. 
   
   Что называется пределом функции?
   
8. 
   Определите понятие предела функции на бесконечности.
   
9. 
   Сформулируйте определения односторонних пределов.
   
10. 
    Сформулируйте первый замечательный предел; второй замечательный предел.
    
11. 
    Что такое бесконечно малые функции? Перечислите их свойства.
    
12. 
    
    Как сравнивают бесконечно малые функции?
    
13. 
    
    Какие бесконечно малые функции называются эквивалентными?
    
14. 
    Запишите цепочку эквивалентных бесконечно малых.
    
15. 
    
    Что называется функцией, непрерывной в точке?
    
16. 
    Что такое точки разрыва функции? Приведите классификацию точек разрыва функции.
    
17. 
    Сформулируйте понятие непрерывности функции на отрезке.
    
18. 
    Перечислите свойства функций, непрерывных на отрезке.
    

Дифференциальное исчисление функций одной переменной

1. 
   
   Что называется производной функции?
   
2. 
   
   В чем состоит геометрический и механический смысл производной?
   
3. 
   
   Чему равна производная суммы, произведения и частного двух функций?
   
4. 
   Запишите формулы дифференцирования степенной и показательной функции.
   
5. 
   
   Что называется логарифмическим дифференцированием?
   
6. 
   
   Как найти производную показательно-степенной функции?
   
7. 
   
   Сформулируйте определение дифференциала. Какой его геометрический смысл?
   
8. 
   
   Как используется дифференциал в приближенных вычислениях?
   
9. 
   Сформулируйте определение производной n-го порядка.
   
10. 
    Запишите формулу Лейбница для производной n-го порядка произведения функций.
    
11. 
    
    Как найти производные первого и второго порядков функции, заданной параметрически; неявной функции?
    
12. 
    Что называется дифференциалом n-го порядка?
    
13. 
    Сформулируйте теорему Ролля. Укажите ее геометрический смысл.
    
14. 
    Сформулируйте теорему Лагранжа. Укажите ее геометрический смысл.
    
15. 
    Сформулируйте правило Лопиталя для раскрытия неопределенностей типа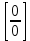 и .
    
16. 
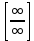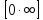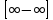    Как раскрываются неопределенности типа и с использованием правила Лопиталя?
    
17. 
    
    Как раскрываются степенные неопределенности с использованием правила Лопиталя?
    
18. 
    Запишите формулу Тейлора с остаточным членом в форме Лагранжа.
    
19. 
    Запишите формулу Маклорена.
    
20. 
    
    Как найти интервалы возрастания и убывания функции?
    
21. 
    
    Какое необходимое условие локального экстремума?
    
22. 
    
    Какие точки называются критическими?
    
23. 
    Сформулируйте достаточное условие существования экстремума функции, связанное с производной первого порядка.
    
24. 
    Сформулируйте достаточное условие существования экстремума функции, связанное с производной второго порядка.
    
25. 
    
    Как найти промежутки выпуклости, вогнутости, точки перегиба?
    
26. 
    
    Как найти вертикальные асимптоты графика функции; наклонные асимптоты?
    
27. 
    
    Как найти наибольшее и наименьшее значение функции на отрезке?
    

---

Дифференциальное исчисление функций нескольких переменных

1. 
   Сформулируйте определение функции n переменных, ее области определения и множества значений.
   
2. 
   
   Сформулируйте определение функции двух переменных и ее области определения. Каков геометрический смысл этих понятий?
   
3. 
   
   Что называется линией уровня функции двух переменных?
   
4. 
   Сформулируйте определение поверхности уровня функции .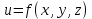
   
5. 
   Сформулируйте определение частных производных функции двух переменных.
   
6. 
   Сформулируйте определение полного дифференциала функции n переменных; двух переменных.
   
7. 
   
   Как используется полный дифференциал в приближенных вычислениях?
   
8. 
   Сформулируйте определение производной по направлению.
   
9. 
   Сформулируйте определение градиента функции.
   
10. 
    
    Как связана производная по направлению с градиентом?
    
11. 
    Определите и укажите правила нахождения производных и дифференциалов высших порядков.
    

Неопределенный интеграл

1. 
   Дайте определение первообразной для функции f(x) на промежутке (a; b).
   
2. 
   График какой первообразной для функции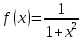 пройдет через точку с координатами (1; 2π)?
   
3. 
   
   Поясните смысл операции «введение под знак дифференциала»?
   
4. 
   Укажите правило применения замены переменной в неопределенном интеграле.
   
5. 
   Запишите формулу интегрирования по частям.
   
6. 
   Что обозначает термин «выделить целую часть неправильной дроби»?
   
7. 
   На какие простейшие дроби раскладывается дробь ?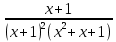
   
8. 
   Как рационализируется интеграл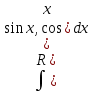 ? Почему подстановка 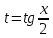называется универсальной?
   
9. 
   Как вычисляется интеграл вида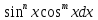 в зависимости от четности и нечетности показателей n и m?
   
10. 
    Как вычисляется интеграл вида ?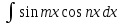
    
11. 
    При помощи каких подстановок можно вычислить интегралы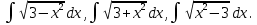
    

---

Определенный интеграл.

1. 
   Дайте определение определённого интеграла, укажите его геометрический смысл.
   
2. 
   Перечислите основные свойства определённого интеграла.
   
3. 
   Запишите формулу Ньютона-Лейбница.
   
4. 
   Укажите правило применения замены переменной в определенном интеграле.
   
5. 
   Выпишите формулу интегрирования по частям для определенного интеграла.
   
6. 
   Дайте определение несобственного интеграла I рода и укажите его геометрический смысл.
   
7. 
   Дайте определение несобственного интеграла II рода и укажите его геометрический смысл.
   
8. 
   Сформулируйте признаки сходимости несобственного интеграла I рода.
   
9. 
   Сформулируйте признаки сходимости несобственного интеграла II рода.
   
10. 
    Как вычислить площадь плоской фигуры с помощью определенного интеграла?
    
11. 
    Как вычислить длину дуги кривой в декартовой системе координат; в полярных координатах; в случае, если кривая задана параметрическими уравнениями?
    
12. 
    Запишите формулу вычисления объёма тела по площадям его параллельных сечений.
    
13. 
    Приведите формулу для объёмов тел вращений вокруг оси Ох, вокруг оси Оу.
    
14. 
    Запишите формулу вычисления площади поверхности тела вращения.
    
15. 
    Как найти массу неоднородного стержня?
    
16. 
    По каким формулам находятся координаты центра тяжести плоской кривой и криволинейной трапеции?
    
17. 
    Запишите формулу для вычисления работы переменной силы F(x).
    

---

Смотрите также файлы

• Коллоидная химия.doc

• Осуществление руководства производственного участка и обеспечение выполнения участком производственных заданий.docx

• Инструкция по выполнению практической работы выберите класс, тему урока в соответствии с прп и заполните.pdf

• азастан тарихы 9 сынып іі нса а блім.doc

• 1. 2 Проблема социализации личности в западных и отечественных психологических и педагогических теориях и концепциях.docx