Сдал: Скворцов И.В.Принял: Каладзе В.А. Дата: ОТЧЁТпо Лабораторной работе № 5(Идентификация модели, линейной относительно параметров, методом наименьших квадратов, Моделирование)Основы теорииВ данной лабораторной работе рассматриваются теоретические основы метода наименьших квадратов (МНК) и методика его применения в задачах математического моделирования, а также методология проведения вычислительного эксперимента на простейшем примере идентичности объекта исследования и его математической модели.Регрессионный анализ – наиболее распространенный статистический инструмент для описания зависимости исследуемой величины от факторов влияния. Искомая регрессионная связь представляет собой полиномиальную зависимостьy = P_n(x) ,степень которой определяется условиями задачи, требованиями и вычислительными возможностями исследователя. На практике обычно используются полиномы не выше второго порядка 2 y L x Q x = + ( ) ( ), где первое слагаемое представляет собой линейную форму, а второе – является квадратичной формой. Идентификацию модели обычно начинают с самой простой линейной формы – линейной суперпозиции компонент двух векторов с соответствующими параметрами модели объекта (коэффициентами уравнения). В дальнейшем, при необходимости, структуру модели уточняют, поэтапно повышая степень полинома. Метод наименьших квадратов (МНК) – это самый известный в этом разделе моделирования метод параметрической идентификации. Схема его применения сводится к трём основным этапам: 1) на основе предварительно решённой задачи структурной идентификации определяется вид соответствующей модели; 2) ставится задача выпуклой оптимизации на базе критерия наименьших квадратов; 3) на основе необходимого условия экстремума формируется и решается система нормальных (приведённых к простейшему виду) уравнений.Этап А. Имитация объекта исследования, как функциональной стохастической системы. Математически это означает

---

, что система представлена в виде детерминированной функции с наложенной на её отклик y% аддитивной помехой наблюдения δ, которая определяется как случайный процесс типа «белый шум». В задачах данного класса случайный процесс можно понимать как случайную величину, отдельные реализации которой регистрируются в моменты измерений. Обычно полагают, что эти моменты времени расположены на временной оси на равном расстоянии друг от друга. Следовательно помеха случайным образом искажает отклик объекта. В данной лабораторной работе рассматривается упрощённая структура объекта, с целью отработки методики проведения вычислительного эксперимента. На этом этапе необходимо сформировать виртуальный объект исследования в виде одномерной линейной зависимости.

y = a*x + b (1.1)

в которую аддитивно вводится случайная помеха δ наблюдения, центрированная с постоянной дисперсией и значениями в моменты времени, соответствующие измерениям. Значения скалярного фактора x определяются квантованием интервала измерения [x ’,x ” ], т.е. в каждый момент времени i, результат наблюдения за откликом объекта имеет вид:

y = y + δ

Этап В. Идентификация модели объекта. В качестве идентифицируемой модели используется линейная зависимость аналогичная выражению (1.1) для нахождения значений параметров a и b которой, следует построить процедуру оценки её параметров, на основе критерия наименьших квадратов

Значения a b, полученные в результате решения этой системы, будут оптимальными оценками параметров модели (1.1). Решить полученную систему уравнений для значений фактора x∈[x ’ , x ” ], при x ” - x ’ = 1 и ∆x = 0.1, любым известным методом, лучше методом Гаусса по правилу исключения переменных. В контрольном примере положить: a = 2, b = 5. В индивидуальных расчётах выбирать значения параметров модели из областей: a ∈ [1, 4], b ∈ [5,8].

Методическая часть

1. Уравнение системы (1.1), указав исходные значения её параметров.

2. Полученную математическую модель (1.1), указав полученные МНК оценки её параметров.

3. Расширенную информационную матрицу.

4. Полученные графики на одном планшете.

5. Выводы.

Результаты:

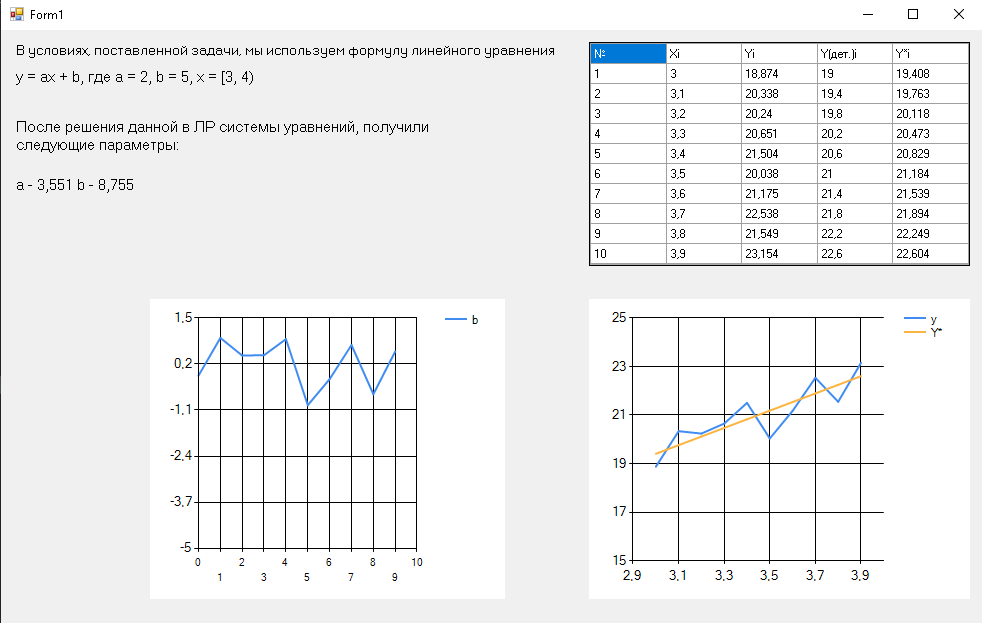
Выводы:

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

---

Смотрите также файлы

• Институт геологии и нефтегазодобычи.docx

• .docx

• Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Ручное практическое задание пнк, кп.rtf

• Методические указания Иллюстрации Бег на прямых ногах. 100 м.docx

• Диагностические возможности методик изучения эмоций.docx