Восприятие информации происходит в три этапа, что соответствует таким стадиям урока:

• 
  подготовительный – стадия вызова;
  
• 
  восприятие нового – смысловая стадия (или стадия реализации смысла);
  
• 
  присвоение информации – стадия рефлексии.
  

   Применение приемов технологии развития критического мышления учащихся на уроках математики.
Прием “Ключевые слова”

Стадию вызова на уроке можно осуществить многими методами, в том числе и хорошо известными, например, "ключевые слова", по которым можно придумать рассказ или расставить их в определенной последовательности, а затем, на стадии осмысления искать подтверждение своим предположениям, расширяя материал.

Например, Закрепление знаний по опорным словам при изучении величин (времени, массы, площади, длины).
Прием “Лови ошибку”

Учитель заранее подготавливает текст, содержащий ошибочную информацию, и предлагает учащимся выявить допущенные ошибки.
Важно, чтобы задание содержало в себе ошибки 2 уровней:

• 
  явные, которые достаточно легко выявляются учащимися, исходя из их личного опыта и знаний;
  
• 
  скрытые, которые можно установить, только изучив новый материал.
  

Учащиеся анализируют предложенный текст, пытаются выявить ошибки, аргументируют свои выводы. Затем изучают новый материал, после чего возвращаются к тексту и исправляют те ошибки, которые не удалось выявить в начале урока.

Например, задачи с ошибками, с неверной информацией.
На стадии вызова наиболее часто используется: Прием «Верные, неверные утверждения».

Учитель зачитывает верные и неверные утверждения, учащиеся выбирают «верные утверждения» из предложенных, обосновывая свой ответ.

 Например, при устном счете

-  Произведение 0 и 9 равно 9;

- Сумма 36 и 14 больше 40;

- Разность 80 и 15 меньше разности 80 и 25.

На стадии рефлексии после изучения нового материала учитель снова возвращает детей к вопросам. Например, при введении понятия «Площадь прямоугольника» на стадии вызов повторяем свойства прямоугольника через игру "Да -  нет"

- Через точку можно провести только одну прямую (нет).

- Прямоугольник - это замкнутая ломаная линия (да).

- Прямоугольник - это четырёхугольник, у которого все стороны равны (нет).

- Треугольник, у которого две стороны имеют равную длину, называется равнобедренным (да).

- Треугольник, у которого один угол острый, называется тупоугольным (нет).

- Площадь - это сумма длин сторон прямоугольника (нет)

---

Прием «Тонкие и толстые вопросы»

Можно использовать на любой стадии урока. Учащиеся учатся задавать вопросы таблице, а потом записывать вопросы по тексту.

Кластер- способ графической организации материала, позволяющий сделать наглядными мыслительные процессы.

Например,

- при изучении геометрических фигур, треугольник, угол – острый, тупой, прямой, имеет вершины и т.д.

- при изучении величин;

- при изучении задач на движение
Также одним из способов развития смыслового чтения является организация работы с текстовыми задачами.

Проводится анализ задачи, устанавливается связь между данным и искомым, прежде чем выбрать то или иное действие для ее решения. Перевод текстовой задачи в таблицу, схему, графическую модель и наоборот. Работе над текстом задачи придается также творческий характер: изменить вопрос или условие, поставить дополнительные вопросы. Что позволяет расширить кругозор ребенка, установить связь с окружающей действительностью. В контексте смыслового чтения при решении задач роль учителя состоит в том, чтобы организовать и направить детей на решение задачи с помощью наводящих вопросов, научить выделять и находить «главные» слова. Это возможно при помощи диалога и в нем участвуют все дети.
Приём «Составление краткой записи задачи»

Формируется умение целенаправленно читать учебный текст, задавать проблемные вопросы, вести обсуждение в группе.
Приём «Составление вопросов к задаче»

Анализ информации, представленной в объёмном тексте математической задачи, формулировка вопросов к задаче, для ответа на которые нужно использовать все имеющиеся данные; останутся не использованные данные; нужны дополнительные данные.
Таким образом на уроках математики можно организовать целенаправленную систематическую работу по развитию приемов смыслового чтения, что будет способствовать реализации системно-деятельностного подхода в обучении и формированию универсальных учебных действий.

п.2.1 написан вообще не верно. Есть понятие "смысловое чтение", есть приемы формирования смыслового чтения без привязки к технологиям (т.к. технологии уже используют частично эти приемы). Вот надо писать про это. Описывать всевозможные приемы, а затем из них выбрать те, которые можно использовать на уроках математики в начальной школе. Вот в этом смысл данного параграфа. Параграф надо переписывать.

---

2.2. Изучение раздела «Математическая информация» с использованием приемов смыслового чтения

название параграфа как в оглавление
Содержание раздела учебной программы «Математическая информация»:
Нахождение, формулирование одного-двух общих признаков набора математических объектов: чисел, величин, геометрических фигур. Классификация объектов по заданному или самостоятельно установленному признаку. Закономерность в ряду чисел, геометрических фигур, объектов повседневной жизни. Верные (истинные) и неверные (ложные) утверждения, содержащие количественные, пространственные отношения, зависимости между числами/величинами.

Конструирование утверждений с использованием слов «каждый», «все». Работа с таблицами: извлечение и использование для ответа на вопрос информации, представленной в таблице (таблицы сложения, умножения; график дежурств, наблюдения в природе и пр.) Внесение данных в таблицу, дополнение моделей (схем, изображений) готовыми числовыми данными. Алгоритмы (приёмы, правила) устных и письменных вычислений, измерений и построения геометрических фигур. Правила работы с электронными средствами обучения (электронной формой учебника, компьютерными тренажёрами).
Анализ заданий по разделу «Математическая информация»:
1 класс.
УМК «Школа 2000» Л. Г. Петерсон


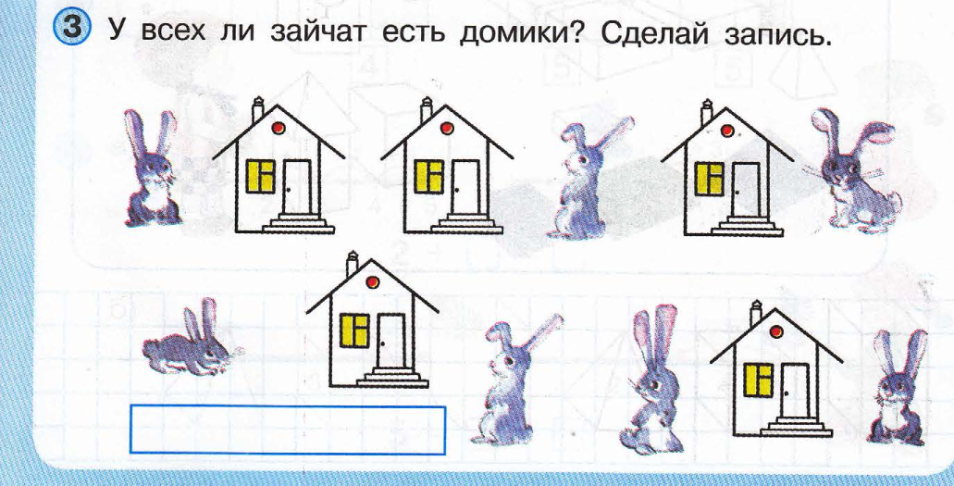
Рис. 1

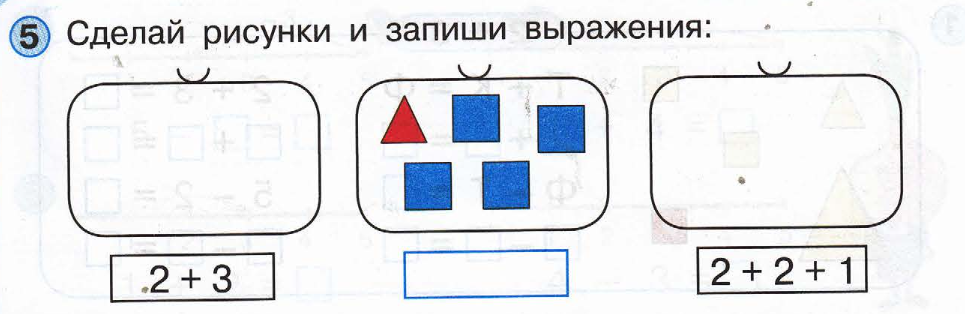
Рис. 2

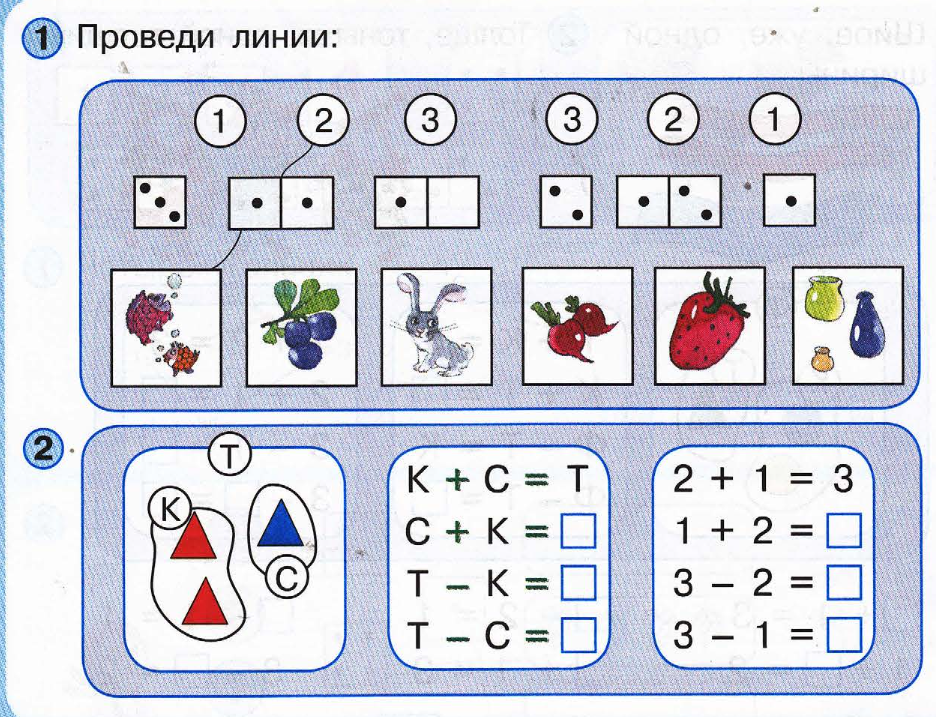
Рис. 3
УМК «Школа России» Моро М.И., Волкова С.И., Степанова С.В.

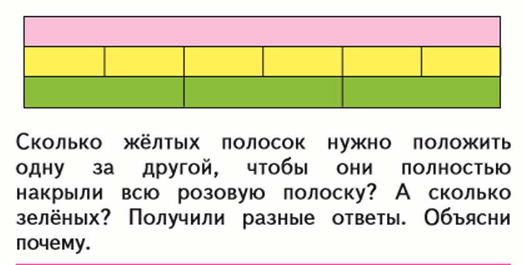
Рис. 4


Рис. 5 - Прием “Ключевые слова”

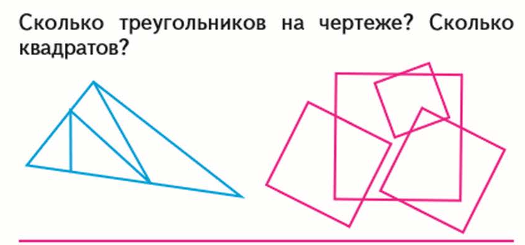
Рис. 6 - Прием «Тонкие и толстые вопросы»

2 класс.
УМК «Школа 2000» Л. Г. Петерсон

---

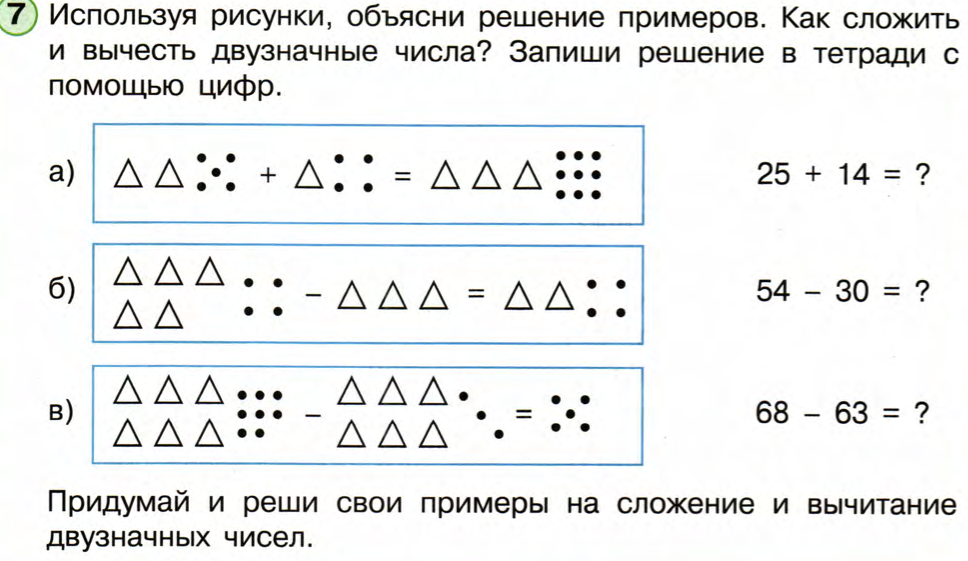
Рис. 7 - Прием «Тонкие и толстые вопросы»

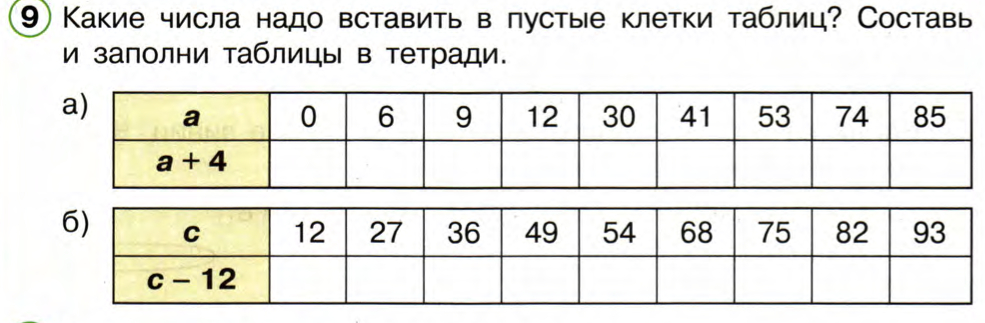
Рис. 8 - Приём «Составление вопросов к задаче»
УМК «Школа России» Моро М.И., Волкова С.И., Степанова С.В.

Рис. 9

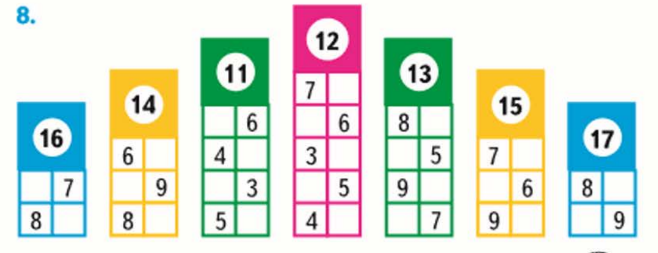
Рис. 10 - Приём «Составление вопросов к задаче»
п.2.2 нет вообще. То что здесь положено вообще не про тему курсовой работы. Параграф надо писать снова.

Выводы - переписываем после доработки главы 2.
Цель смыслового чтения— максимально точно и полно понять содержание текста, все детали и практически осмыслить извлеченную информацию. Это внимательное вчитывание и проникновение в смысл с помощью анализа текста. Когда человек действительно вдумчиво читает, то у него обязательно работает воображение, он может активно взаимодействовать со своими внутренними образами. Человек сам устанавливает соотношение между собой, текстом и окружающим миром. Владение смысловым чтением — это метапредметное умение, которое затрагивает как учебную деятельность обучающихся, так и их повседневную жизнь, потому что тесно связано с формированием их информационной культуры.
Разобрав задачи по разделу «Математическая информация» УМК «Школа России» и «Школа 2000» увидели, что к большей части математических задачи можно подобрать свой прием смыслового чтения на уроке математики.


Заключение

написано неверно. Заключение пишется в соответствии с введением. По тем задачам, что были сформулированы. Отвечаем на вопросы, что было сделано для решения первой задачи, второй и т.д. В конце делаем вывод о достижении цели. Надо переписывать.
В начальной школе изучение математики имеет особое значение в развитии младшего школьника. Приобретённые им знания, опыт выполнения предметных и универсальных действий на математическом материале, первоначальное овладение математическим языком станут фундаментом обучения в основном звене школы, а также будут востребованы в жизни.
В начальной школе математические знания и умения применяются школьником при изучении других учебных предметов (количественные и пространственные характеристики, оценки, расчёты и прикидка, использование графических форм представления информации). Приобретённые учеником умения строить алгоритмы, выбирать рациональные способы устных и письменных арифметических вычислений, приёмы проверки правильности выполнения действий, а также различение, называние, изображение геометрических фигур, нахождение геометрических величин (длина, периметр, площадь) становятся показателями сформированной функциональной грамотности младшего школьника и предпосылкой успешного дальнейшего обучения в основном звене школы.

---

Технология деятельностного метода обучения – это метод обучения, при котором ребенок не получает знания в готовом виде, а добывает их сам в процессе собственной самостоятельной учебно-познавательной исследовательской деятельности. Задача педагога при введении нового материала заключается не в том, чтобы все наглядно и доступно объяснить, показать и рассказать. Педагог должен организовать исследовательскую работу детей, чтобы они сами додумались до решения проблемы урока и сами объяснили, как надо действовать в новых условиях.
Данный подход направлен на развитие каждого ребенка, на формирование его индивидуальных способностей, а также позволяет значительно упрочнить знания и увеличить темп изучения материала без перегрузки обучающихся. При этом создаются благоприятные условия для их разноуровневой подготовки, реализации принципа моделирования.
Цель смыслового чтения— максимально точно и полно понять содержание текста, все детали и практически осмыслить извлеченную информацию. Это внимательное вчитывание и проникновение в смысл с помощью анализа текста. Когда человек действительно вдумчиво читает, то у него обязательно работает воображение, он может активно взаимодействовать со своими внутренними образами. Человек сам устанавливает соотношение между собой, текстом и окружающим миром. Владение смысловым чтением — это метапредметное умение, которое затрагивает как учебную деятельность обучающихся, так и их повседневную жизнь, потому что тесно связано с формированием их информационной культуры.
Разобрав задачи по разделу «Математическая информация» УМК «Школа России» и «Школа 2000» увидели, что к большей части математических задачи можно подобрать свой прием смыслового чтения на уроке математики.
Тем самым, в ходе выполнения работы были выполнены все ранее поставленные задачи, а именно:

1. 
   Проанализировать содержание начального курса математики
   
2. 
   Изучить современный урок математики, соответствующий ФГОС
   
3. 
   Разобрать и изучить приемы смыслового чтения, используемые в начальной школе на уроке математики
   
4. 
   Изучить раздел «Математическая информация» с использованием приемов смыслового чтения
   

Библиографический список

список литературы очень маленький, не соответствует требованиям. Должно быть в курсовой работе не менее 20-25 источников. Причем на все источники из этого списка должны быть ссылки во всей работе.

---

Смотрите также файлы

• Решение Запишем координаты вектора начальной скорости Запишем координаты вектора ускорения.docx

• Программа среднего профессионального образования Название Право и организация социального обеспечения соо.docx

• 1. Раскройте правила соревнований любого вида единоборств.docx

• Сыбайлас жеморлы.pptx

• "Бизнес план ивестиционного проекта" выполнила Горбань А. С.docx