Файл: Контрольная работа по дисциплине Моделирование процессов и систем студент гр. Итб33010220 Никитина А. А.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 25
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Институт математики и информационных систем
Факультет автоматики и вычислительной техники
Кафедра систем автоматизации управления
Контрольная работа
по дисциплине
«Моделирование процессов и систем»
Выполнил:
студент гр.
ИТб-3301-02-20
Никитина А.А.
Проверил:
Поздин В.Н.
Киров 2021
ЗАДАНИЕ 1
Для заданного варианта САР (рис. 1) операторным методом получить выражение для переходной характеристики h(t). Построить переходный процесс в виде графика (25 -30 точек), привести таблицы расчетов.
Рисунок 1 Структурная схема САР
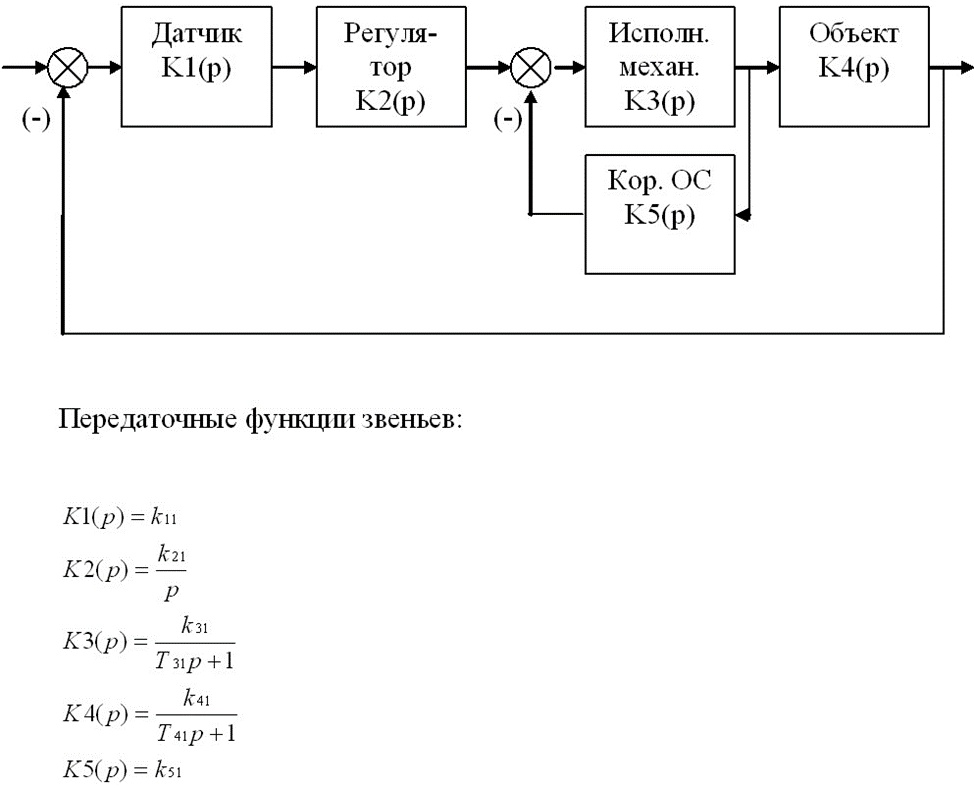
ВАРИАНТ
k11 = 2,5 k21= 1,2 k31 = 0,355 k41 = 3 k51 = 0,8
T31 = 0,5 T41 = 0,4
1. Поиск выражения для общей передаточной функции ????(????) всей цепи
а) последовательное соединение ????1(????) и ????2(????):
????1(????) = 2,5
????2(????) =
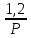
????12(????) = ????1(????) ∗ ????2(????) =
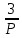
б) отрицательная обратная связь ????3(????) и ????5(????):
????3(????) =
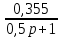????5(????) = 0,8 ????35(????) =
= 
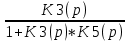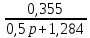
в) последовательное соединение ????12(????) и ????35(????):
????15(????) = ????12(????)∗????35(????) =
=
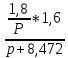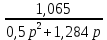
г) учитывая все соединения блоков, получим ????(????):
????4(????) =
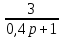
????(????) = ????15(????) *
= 
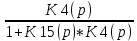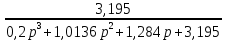
2. Найдём корни характеристического полинома в знаменателе передаточной функции A(pi) =
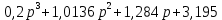
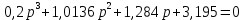
????1 = … = -0.317651+ 1.871630*???? =
= 1.898394 *
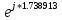= = 1.898394 *
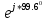
????2 = … = -0.317651- 1.871630*???? =
= 1.898394 *
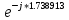= = 1.898394 *
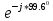
????3 = … = -4.432698
3. Найдём производные от различных корней характеристического полинома A(pi) =
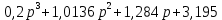
A'(pi) =
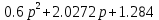
A'(????1) = …= -1.401200 + 3.080738 *j=
= 3.384421 *
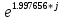=A'(????2) = …= -1.401200 – 3.080738 *j =
= 3.384421 *
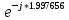=A'(????3) = …= 4.087321
4. Рассчитаем составляющие разложения
Воспользуемся формулой разложения Карсона - Хевисайда для данной САР:
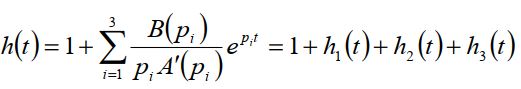
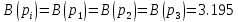
а)
= 
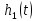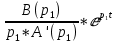= …= = 0.497278 *
* 
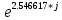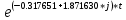== 0.497278 *
* 
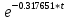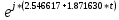=б)
= 
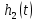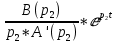= …= = 0.497278 *
* 
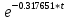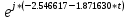
в)
= 
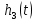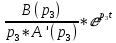= …= 0.1763453*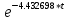 
5. Получим выражение переходной характеристики h(t) для данной САР
а) Исключаем комплексные экспоненты по формуле:
+ 
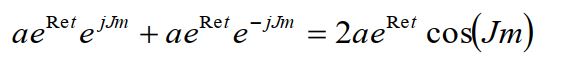
= 2*0.497278 *
*cos (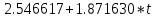
) = = 0.994556 *
* cos (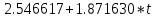 )б) ℎ(????) = 1 + ℎ1(????) + ℎ2(????) + ℎ3(????)
ℎ(????) = 1 – (0.176345*
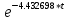) + 0.994556 * * *cos (
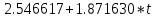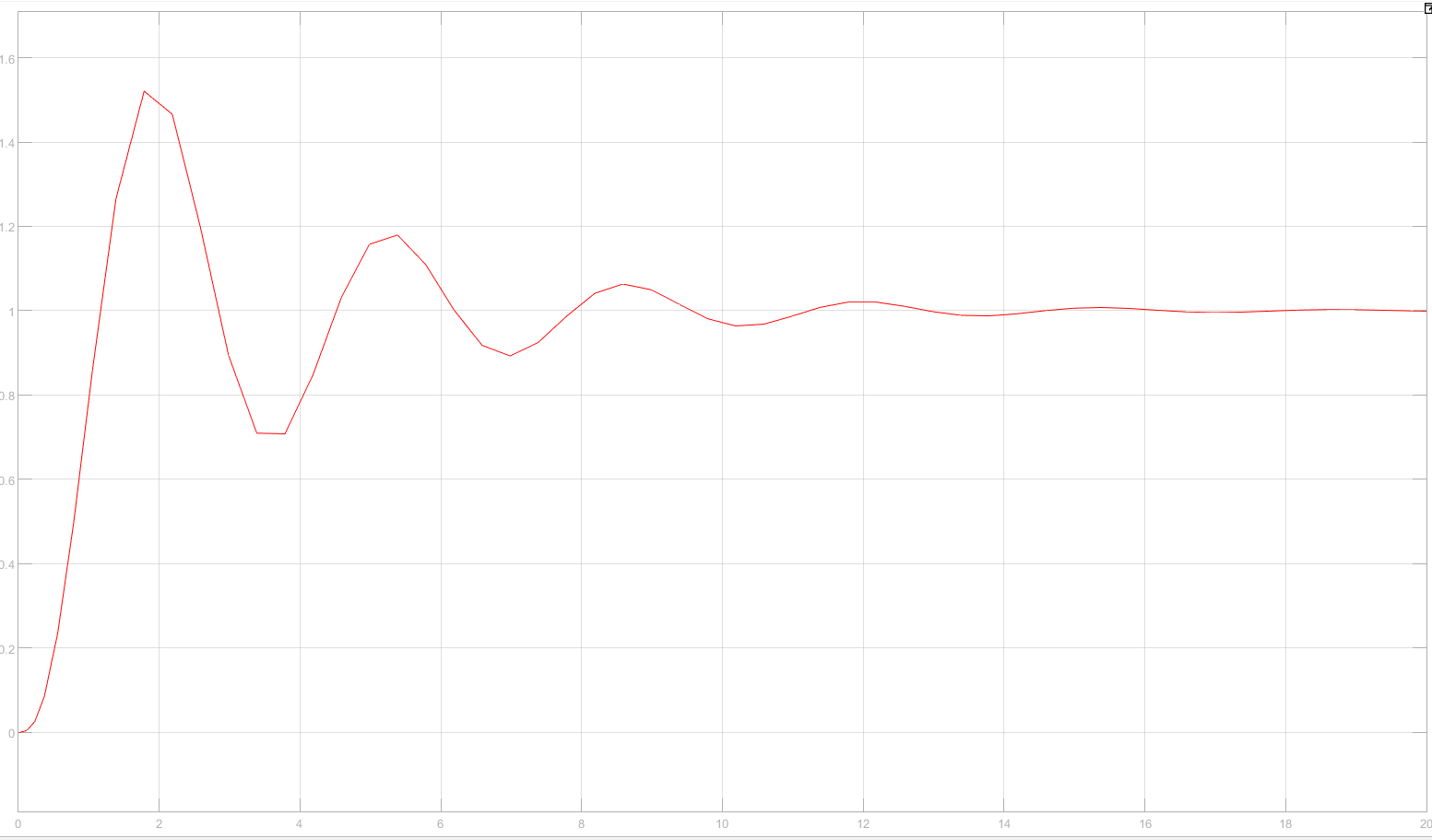
)6. Строим график переходного процесса
Таблица расчёта точек
| № | t, c | h | № | t, c | h | № | t, c | h |
| 1 | 0 | 0.000000 | 10 | 5 | 1.160302 | 19 | 12 | 1.021811 |
| 2 | 1 | 0.788034 | 11 | 5.5 | 1.166857 | 20 | 13 | 0.997225 |
| 3 | 1.5 | 1.369419 | 12 | 6 | 1.052200 | 21 | 14 | 0.989641 |
| 4 | 2 | 1.526854 | 13 | 6.5 | 0.931384 | 22 | 15 | 1.005938 |
| 5 | 2.5 | 1.264204 | 14 | 7 | 0.892558 | 23 | 20 | 0.998871 |
| 6 | 3 | 0.883913 | 15 | 8 | 1.018691 | 24 | 25 | 1.000212 |
| 7 | 3.5 | 0.690202 | 16 | 9 | 1.048857 | 25 | 30 | 0.999961 |
| 8 | 4 | 0.770946 | 17 | 10 | 0.969023 | 26 | 40 | 0.999999 |
| 9 | 4.5 | 0.993661 | 18 | 11 | 0.987478 | 27 | 50 | 0.999999 |
7. Рассчитываем показатели качества САР
а) Установившееся состояние.
По графику переходного процесса видно, что ℎуст. = 1. Для проверки можно подставить заведомо большой показатель времени в выражение для переходной характеристики ℎ(????):
при t = 100 сек ℎ(????) = 1.000000
б) Перерегулирование.
На графике переходного процесса ℎмакс = 1.520563
???? =
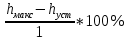= 52.0563%в) Время регулирования.
На графике данного переходного процесса при Δ = 0,05 переходная характеристика входит в “коридор” [(ℎуст – Δ), (ℎуст + Δ)] в точке t = 16.
Значит, ????р = 16 сек.
г) Степень устойчивости.
Степень устойчивости ???? определяется отношением количества корней к модулю минимальной действительной части корней.
???? =
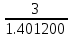= 2.141021981159ЗАДАНИЕ 2
Для данного варианта САР методом вспомогательной переменной получить систему дифференциальных уравнений в нормальной форме Коши.
Передаточная функция по данному варианту имеет вид:
????(????) =
= 
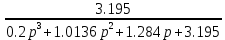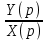
где ????(????) – выходной сигнал, ????(????) – входной сигнал. Это уравнение можно записать в следующем виде:
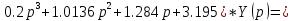3.195 * X(p) Учитывая, что все дифференциальные операторы при входной и выходной величинах и обратные им операторы коммутативны, запишем его в виде:
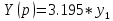
X(p) = (
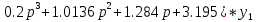
Введём обозначения:
????̇1 = ????2
????̇2 = ????3
Учитывая их, получаем:
????̇3 = − (1.0136????3 + 1.284????2 + 3.195????1) + ????
Объединяя уравнения, полученные выше, получаем систему уравнений в нормальной форме Коши:
????̇1 = ????2
{ ????̇2 = ????3
????̇3 = − (1.0136????3 + 1.284????2 + 3.195????1) + ????
Выходная переменная и новые переменные связаны уравнением
???? = 3.195*????1, которое называется уравнением связи. После всех преобразований исходного уравнения передаточной функции с нулевыми начальными условиями получилась система непрерывной модели САР:
????̇1 = ????2
{ ????̇2 = ????3
????̇3 = − (1.0136????3 + 1.284????2 + 3.195????1) + ????
???? = 3.195*????1
Данное преобразование получило название метода вспомогательной переменной.