ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 13
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
"САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "ЛЭТИ""
ИМ. В.И.УЛЬЯНОВА (ЛЕНИНА)
Кафедра МИТ
ОТЧЕТ
По индивидуальному домашнему заданию №2
Тема: Основные положения квантовой механики
Вариант 8
Студент группы 1104: Кадол Г.Ю.
Преподаватель: Рассадина А.А.
Санкт-Петербург
2022
Задание №1: 1) Рассчитать волну де Бройля для частицы массой m, движущейся со скоростью v, используя формулу
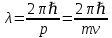
Где ???? – длина волны, которую можно сопоставить с частицей; волновой вектор k направлен по движению частицы, ℏ- квант действия, равный отношению постоянной Планка h к 2π (
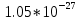эрг*сек).2) Определить ошибку в определении физической величины, налагаемой соотношением неопределенности Гейзенберга, используя формулу
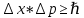
При выполнении заданий обратить особое внимание на правильность применения размерности величин.
Дано:
М=100(г)=0.1(кг)
V=1*
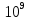(м/с)Решение: Гипотеза де Бройля гласит, что не только фотоны обладают волновыми свойствами, но и все частицы материи. Количественные соотношения, связывающие согласно гипотезе де Бройля корпусколярные и волновые свойства частиц: 1)
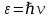
2)
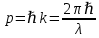
3)
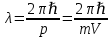
Расчет волны де Бройля:
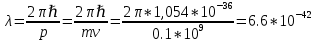мСогласно принципу неопределённости у частицы не могут быть
одновременно точно измерены положение и скорость (импульс). Принцип
неопределённости уже в виде, первоначально предложенном Гейзенбергом,
применим и в случае, когда не реализуется ни одна из двух крайних ситуаций.
Ошибка в определении физической величины, налагаемой соотношением неопределенности Гейзенберга:
Расчет неопределенности координаты частицы:
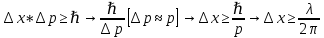, где ????- длина волны де Бройля, которая равна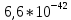 
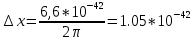мЗадание №2: Рассчитать неопределенность в энергии частицы в соответствии соотношением неопределенности Гейзенберга.
Дано:
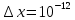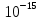см=
мРешение: Расчет неопределенности в энергии части
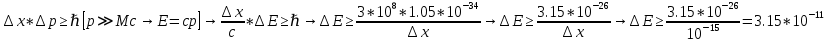Дж=31.5 пкДж , где
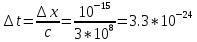c.Вывод: Была рассчитана волна де Бройля для заданных параметров λ=
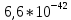м, так же рассчитана неопределенность координаты данной частицы, согласно принципу неопределенности Гейзенберга Δ x⩾
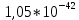м. Можно сказать, что чем больше импульс частицы, тем меньше длина волны де Бройля, в данном случае длина волны слишком мала для их обнаружения.Была рассчитана неопределенность в энергии частицы в соответствии
соотношением неопределенности Гейзенберга Δ E⩾31,5 пкДж, при
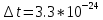c.Данные полученные во второй задаче можно трактовать 3 способами:
1.
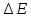- неопределённость энергии состояния микрообъекта, прибывающего в этом состоянии времени 
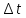.2 .∆Е – неопределенность энергии микрообъекта в некотором процессе длительностью
.
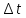
3.
– максимальная точность определения энергии квантовой сиситемы, достижимая путём процесса измерения, длящегося временем 
.