Файл: Задача Записать множество EAB, если А2, 4, 6, 8, 10, 12, B3, 6, 9, 12. Решение Е6, 12.docx
Добавлен: 07.11.2023
Просмотров: 1819
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1. Записать множество Е, если E=A∪B, причем А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Решение:
E=A∪B есть не что иное, как объединение множеств А и В, т.е. множество Е будет состоять из элементов, принадлежащих как множеству А, так и множеству В: Е={2, 3, 4, 6, 8, 9, 10, 12}.
Задача 2. Записать множество E=A⋂B, если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Решение:
Е={6, 12}.
Задача 3. Записать множество E=A\B, если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Решение:
E={2, 4, 8, 10}.
Задача 4. Записать множество
, если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.Решение:
Е={3, 6, 9, 12}.
Задача 5. Проиллюстрировать с помощью кругов Эйлера следующую формулу: E=A\(B∪C).
Решение:
Выполняя действие в скобках (B∪C)=E получим:
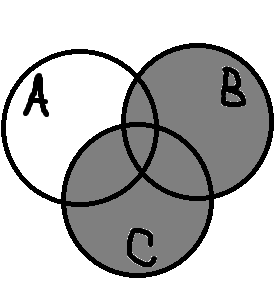
После этого получаем А\Е т.е. необходимо выделить участок множества А, не принадлежащий множеству Е. Ответ примет форму:
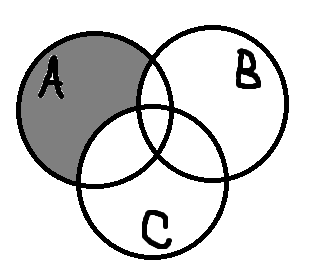
Задача 6. Проиллюстрировать с помощью Диаграмм Венна верность тождества:
.Решение:
Проиллюстрируем левую часть тождества, обозначив сначала объединение множеств В и С,
затем пересечение множеств А и
. Окончательный вид левой части:
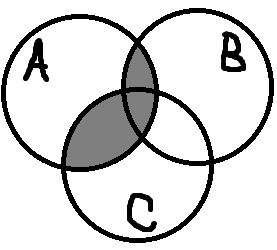
Теперь проиллюстрируем правую часть:
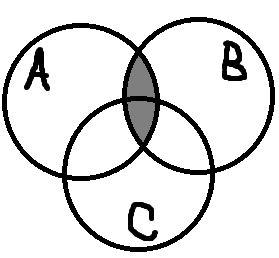
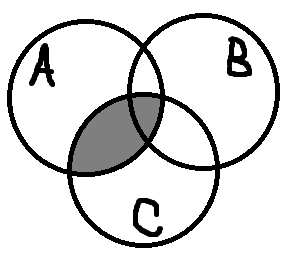
Окончательный вид правой части:
Как видим диаграммы совпадают, следовательно тождество верно.