МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЙВ данном разделе приведены образцы выполнения заданий, содержащихся в контрольных работах.Задания 11 – 20 Для решения задач 11 – 20 рекомендуется учебное пособие [5]Гл. I –IV, стр.39 – 91. В пирамиде SABC: треугольник АВС – основание пирамиды, точка S – ее вершина. Даны координаты точек A, B, C, S. Сделать чертеж. Найти:

1. 
   длину ребра АВ;
   
2. 
   угол между ребрами АВ и AS;
   
3. 
   угол наклона ребра AS к основанию пирамиды;
   
4. 
   площадь основания пирамиды;
   
5. 
   объем пирамиды;
   
6. 
   уравнение прямой АВ;
   
7. 
   уравнение плоскости АВС;
   
8. 
   проекцию вершины S на плоскость АВС;
   
9. 
   длину высоты пирамиды
   

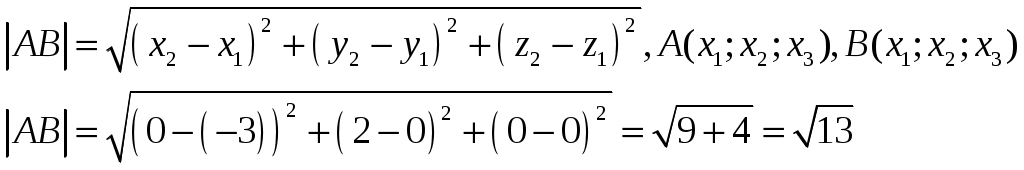
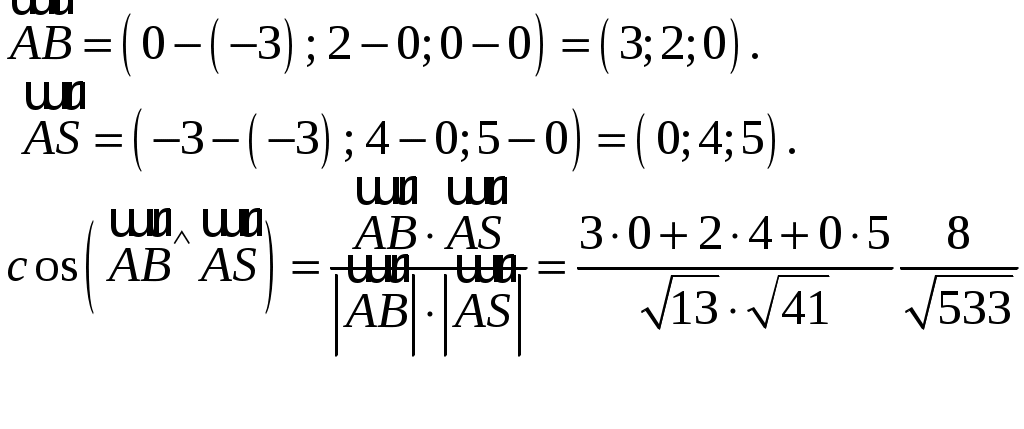
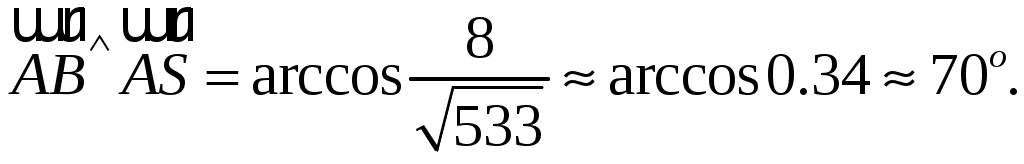
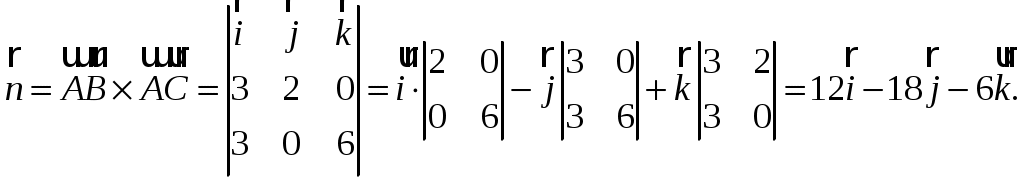
SABC: А(-3;0;0); В(0;2;0); С(0;0;6); S(-3;4;5).Решение1) Длину ребра АВ находим по формуле расстояния между двумя точками:2) Угол между рёбрами найдём по формуле косинуса угла между векторами , координаты которых определяются так:3) Найдем координаты вектора _{Найдем координаты вектора} Он перпендикулярен плоскости (грани) ABC, поэтому угол 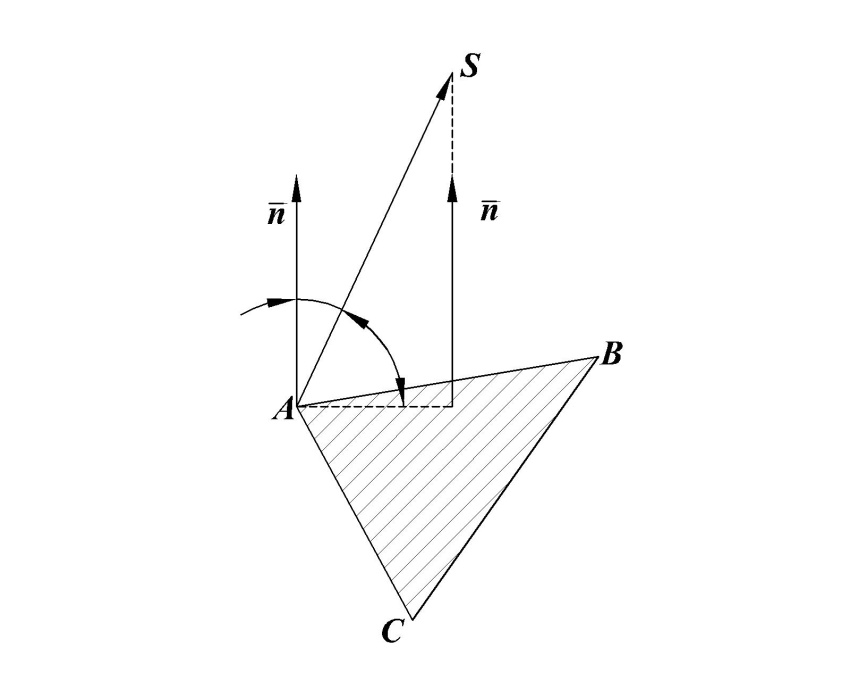между ребром AS и гранью ABC является дополнительным к углу α между векторами _α

---

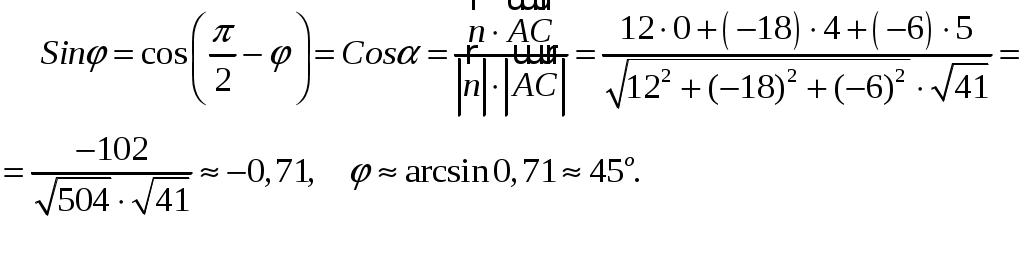
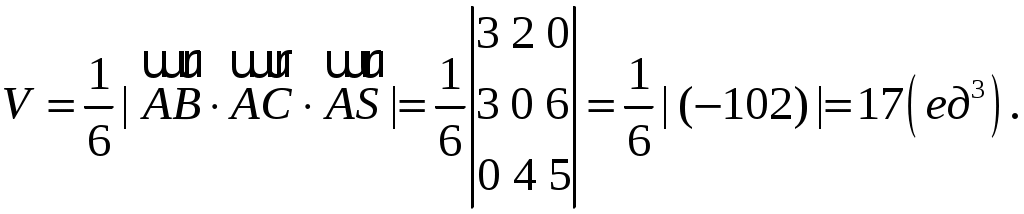
_{φ Отсюда получаем} 4) Площадь определяем с помощью векторного произведения: ,5) Объём пирамиды находится через вычисление смешанного произведения векторов Изучите понятие смешанного произведения, формулу объёма пирамиды и формулу для вычисления смешанного произведения трёх векторов. 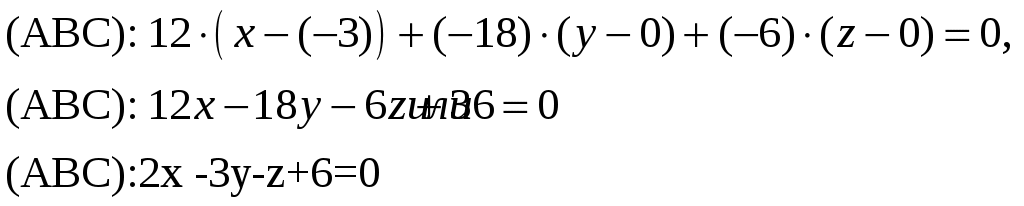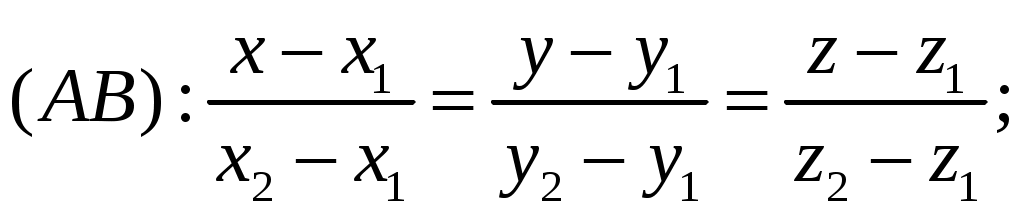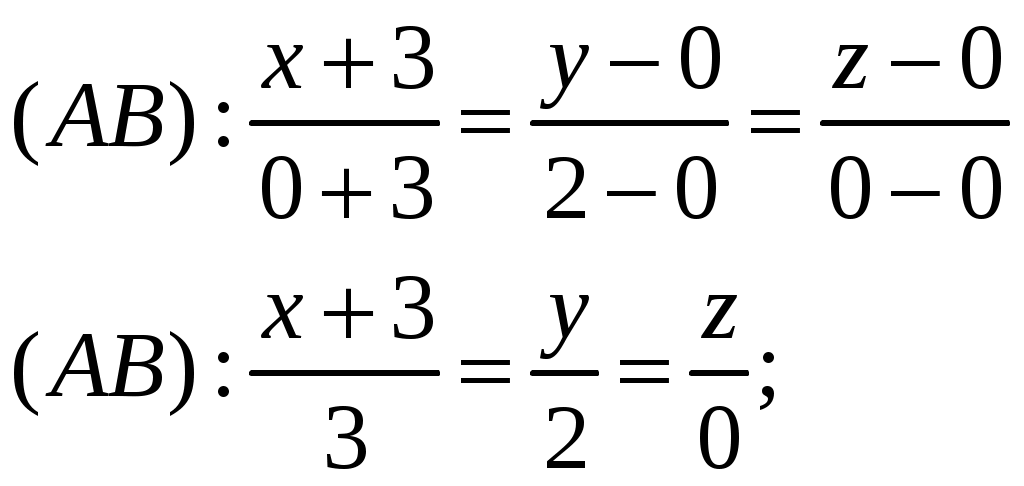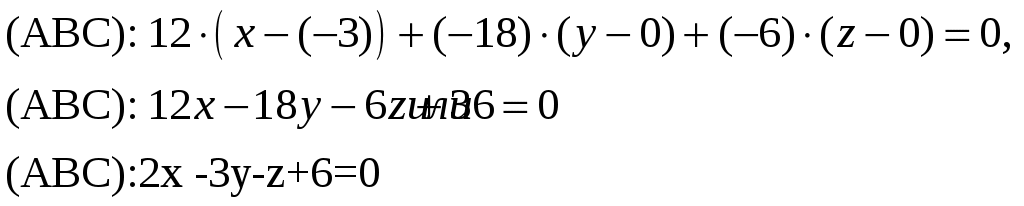Формула для нахождения объема V пирамиды:7) Запишем уравнение плоскости (ABC) перпендикулярной вектору , проходящей через точку А(-3;0;0)6) Уравнение прямой _{, проходящей через точки}Канонические уравнения прямой, вектор направляющий вектор прямой 7) Запишем уравнение плоскости (ABC) перпендикулярной вектору , проходящей через точку А(-3;0;0)8) Для определения проекции вершины на плоскость

---

выполняютсяследующие действия:

а) составляется уравнение высоты пирамиды .

б) находится точка пересечения высоты и основания решением системы, содержащей уравнение высоты и уравнение плоскости.

Решение: SO –высота пирамиды, перпендикулярна плоскости (ABC), следовательно, прямая (SO) параллельна вектору или - нормали плоскости (ABC.

Он будет направляющим для 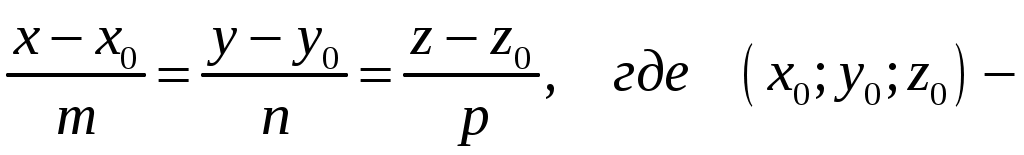По уравнению координаты вершины , т.е.

. Так как точка О – пересечение прямой (SO) и плоскости (ABC), то ее координаты удовлетворяют системе уравнений

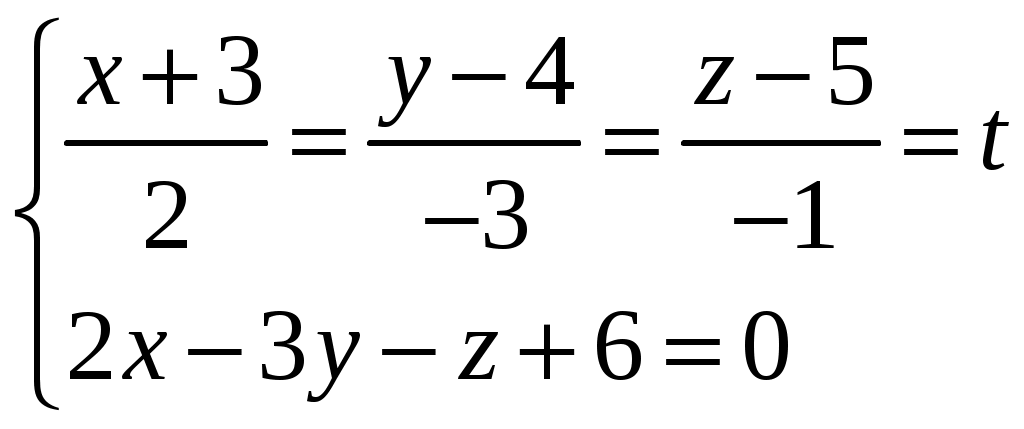, которую можно решить подстановкой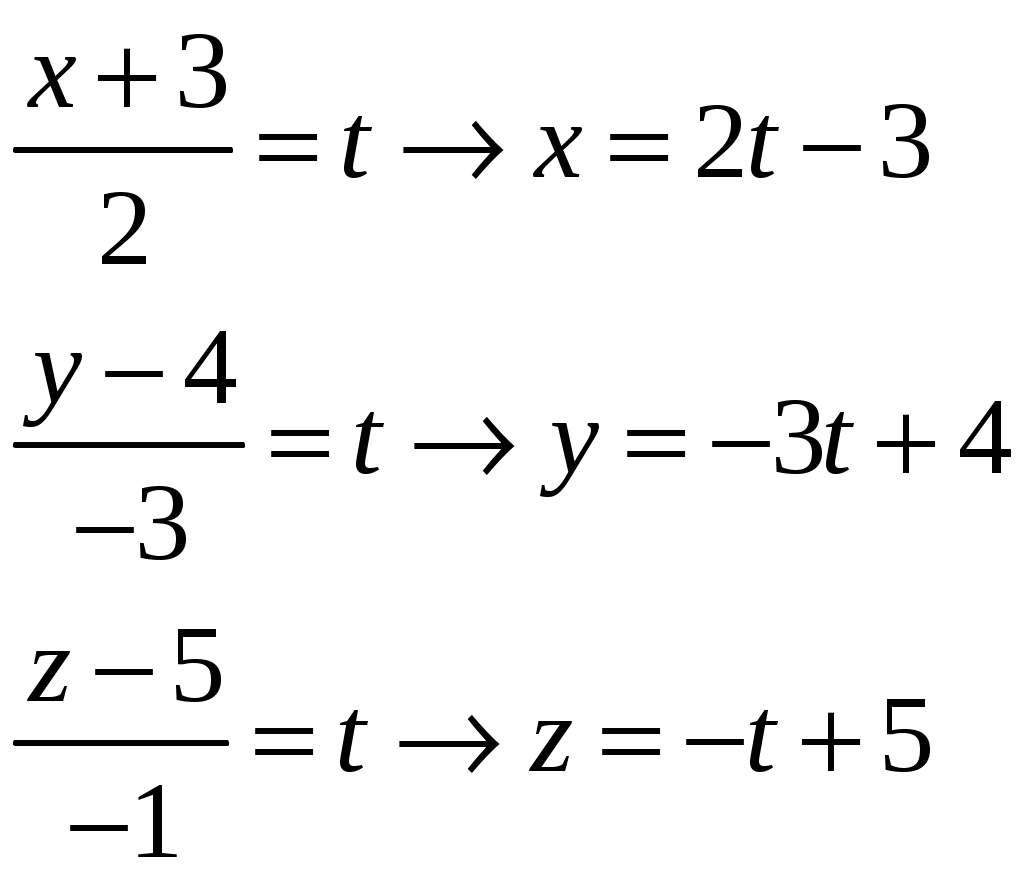



Подставив во второе уравнение, найдём значение , и следовательно значения







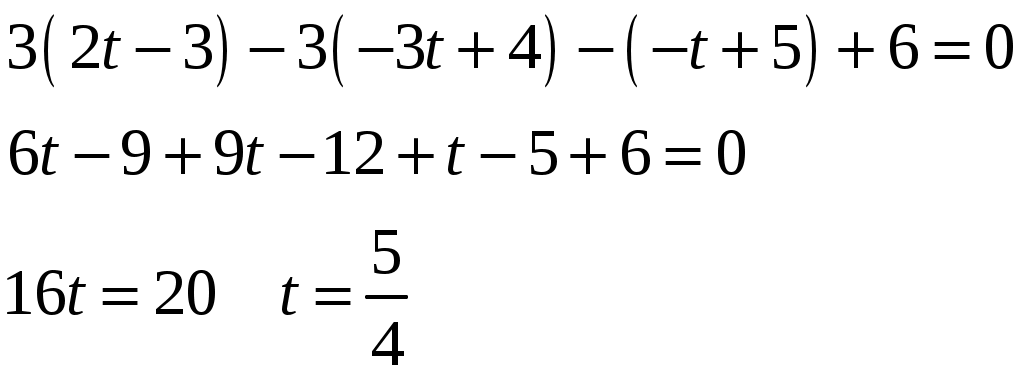
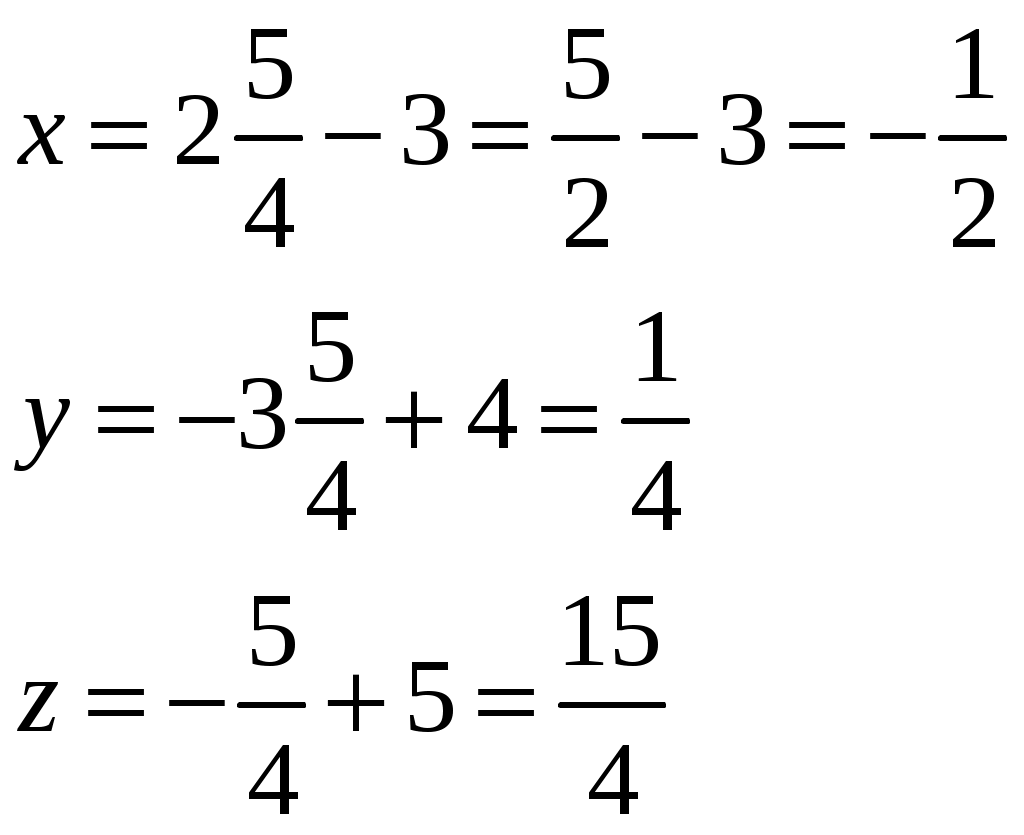
Точка 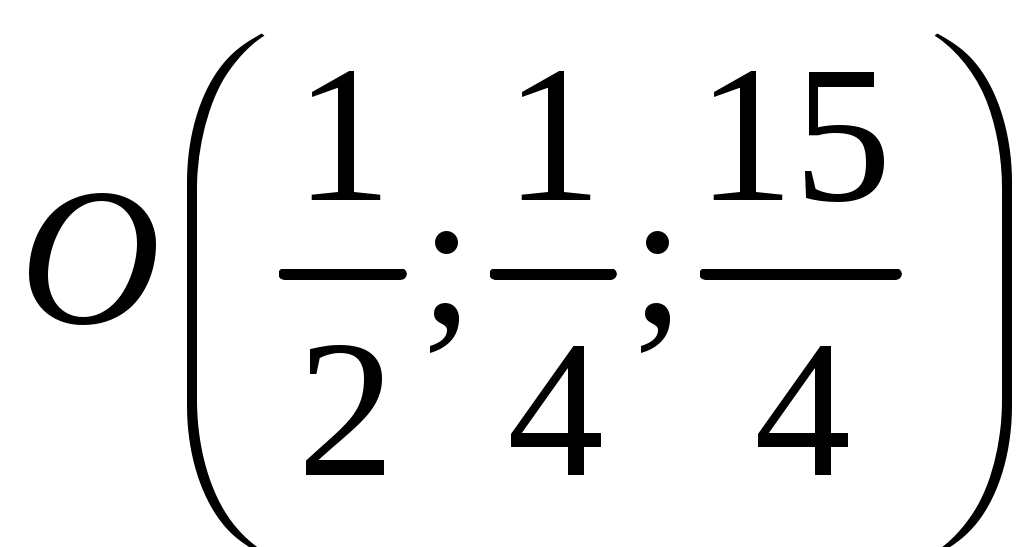- проекция точки

---

на плоскость

9) Длину высоты пирамиды можно найти по формуле расстояния между точками S и O или по формуле расстояния d от точки до плоскости :



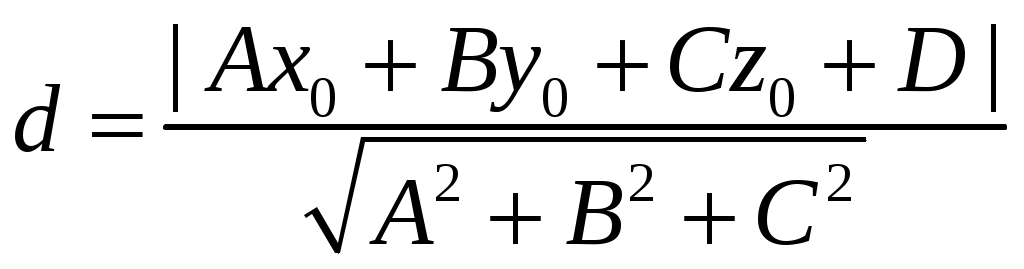
Изучите формулы самостоятельно, решив задание 9).

---

Смотрите также файлы

• О системе работы учителя русского языка и литературы Мислимовой Фариде Себзалиевне с родителями.docx

• Решение Согласно ст. 1066 ук рф не подлежит возмещению вред, причиненный в состоянии необходимой обороны, если при этом не были превышены ее пределы..docx

• Лекция 1 психология часть психология как наука. Предмет и задачи психологии.pptx

• Программа среднего профессионального образования Право и организация социального обеспечения. Дисциплина Гражданское право (Часть 2) Практическое задание 5.pdf

• Предмет Основы слесарного дела.doc