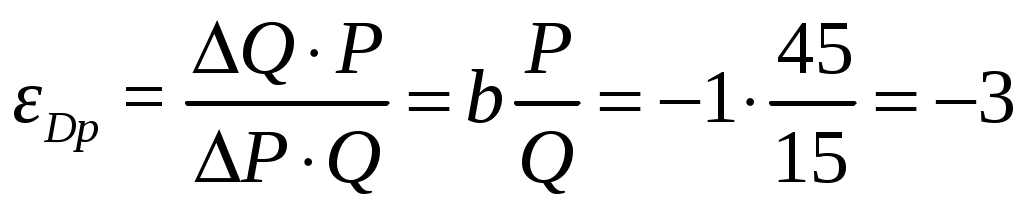Файл: Бланк выполнения практического задания 5 Задачи.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 07.11.2023

Просмотров: 11

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Бланк выполнения практического задания 5

Задачи

1. Предположим, что на рынке действуют две фирмы, функции общих издержек заданы уравнениями: и . Рыночный спрос описывается функцией:

,

где .

Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:

- фирмы конкурируют по Курно;

- фирмы конкурируют по Бертрану;

- фирмы конкурируют по сценарию Штакельберга.

Изобразите решение на графике.

Решение

  1. Стратегия по Курно предполагает, что количественную конкуренцию компаний, которые принимают решение о выпуске самостоятельно.

Решение задачи по Курно:

Прибыль предприятия

П1 =q1*(1000-0.25*(q1+q2)) - 20 + q12

П2=q2(1000-0.25*(q1+q2)) - 20 + 0.25q22

П1 = 1000*q1-0.25*q1*q2 - 20 + 0.75q12

П2=1000*q2-0.25*q1*q2- 20

Найдем производную прибыли каждой фирмы и приравняем к 0

П1' = 1000 -0.25* q2 + 1.5q1 = 0

П2'=1000 - 0.25*q1 = 0

1000 - 0.25*q1 = 0

q1 = 1000 / 0.25 = 4000

1000 - 0.25*q2 + 1.5*4000 = 0

q2 = 7000 / 0.25 = 28 000

P = 1000 - 0.25*(4000 + 28 000) = -7000

Так как выпуск первой фирмы полностью будет продаваться по цене 0, то данная функция не имеет решения в стратегии Курно.

Представим это графически.



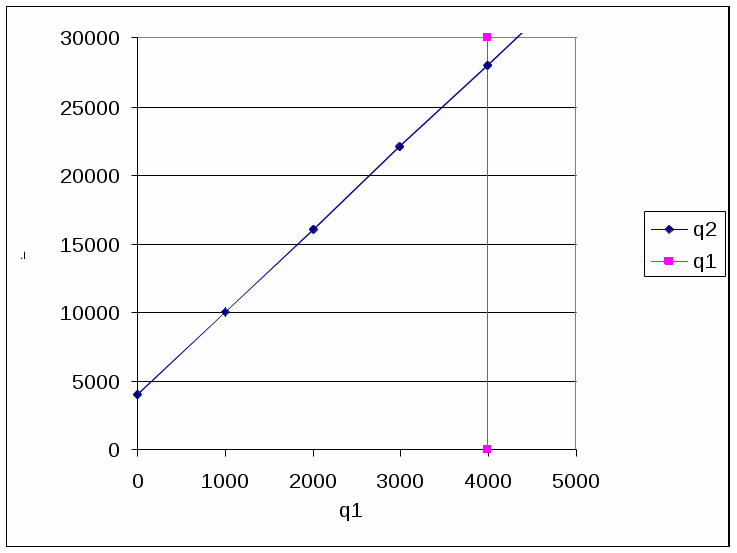
Рисунок 5.1

  1. Стратегия по Бертрану предполагает, что если фирма 1 ожидает, что фирма 2 будет устанавливать цену, не превышающую предельных издержек MC, то её наилучшим ответом является установление цены, равной предельным издержкам.

В соответствии с данным условием решение задачи по Бертрану принимает вид:

MC1 = 2q1

1000 - 0,25q1 = 2q1

2.25q1= 1000

q1 = 1000 / 2.25 = 444,44

MC2 = 0,5q2

1000 - 0,25q2 = 0,5q2

0.75q2= 1000

q2 = 1000 / 0.75 = 1333,33

Общий выпуск 444,44 + 1333,33 = 1777,77


Цена Р = 1000 - 0,25 * 1777,77 = 555,56 ед.

Представим это графически



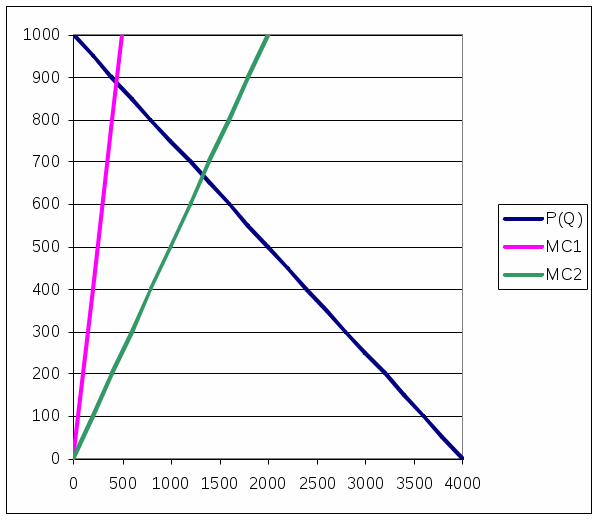
Рисунок 5.2

  1. Стратегия по Штакельбергу предполагает, что одна фирма выступает в роли лидера, а вторая последователя.

Решение задачи по сценарию Штакельберга принимает вид:

Тогда прибыль первой фирмы с учётом уравнения реакции фирмы 2 будет равна:

П1 =q1*(1000-0.25*q1) - 20 + q12

П1 =1000*q1 - 20 + 0,75q12

Она достигает максимума при

П1' = 0

1000+ 1,5q1 = 0

Уравнение не имеет решение в положительных числах.

В случае лидерства фирмы 2 её прибыль будет равна:

П2=q2(1000-0.25*q2) - 20 + 0.25q22

П2=1000*q2 - 20

П2' = 0

1000 = 0

Решения нет.



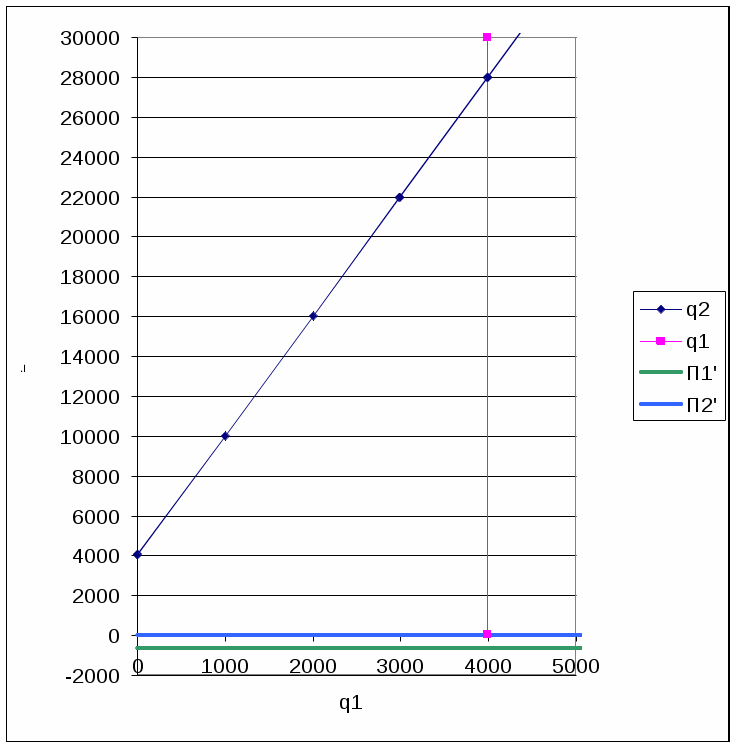
Рисунок 5.3

Вывод: В данных моделях так как издержки имеют отрицательную зависимость от объема производства решение возможно только по Бертрану.


  1. График предельных издержек фирмы-монополиста задан условием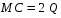 . Функция предельного дохода принимает вид: 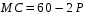. Определите эластичность рыночного спроса 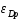при оптимальном выпуске фирмы-монополиста.

Решение

  1. Определяем оптимальный выпуск фирмы-монополиста:

MC = MR

  1. Выводим функцию спроса фирмы-монополиста:



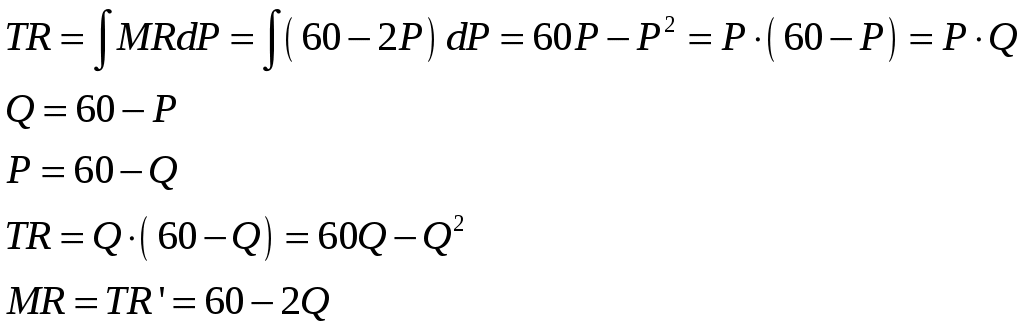
2Q = 60-2Q

4Q = 60

Q = 15

  1. Цена при оптимальном выпуске фирмы-монополиста составит … .

P = a - b*Q P = 60 - Q = 60 - 15 = 45

  1. Эластичность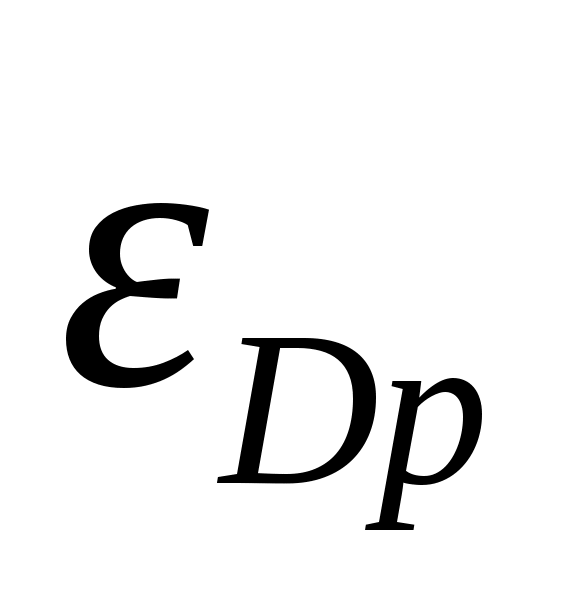 в точке

Смотрите также файлы