Файл: Лабораторной работы Расчет сложной цепи постоянного тока.docx
Добавлен: 07.11.2023
Просмотров: 149
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

РТКП.461531.002 ТУ
1 Цели и задачи
Основная задача выполнения – это самостоятельное освоение и закрепление пройденного материала по теме лабораторной работы «Расчет сложной цепи постоянного тока».
Основное направление – изучение методов расчета сложной цепи постоянного тока. Лабораторная работа включает в себя составление системы уравнений по законам Кирхгофа, расчет токов методом контурных токов, составление баланса мощностей, расчета потенциалов всех точек и напряжения на элементах, построения потенциальной диаграммы, моделирование схемы, разработку программы в пакете Mathcad, расчет относительной погрешности токов и напряжений, расчет схемы методом наложений.
Полученные в ходе выполнения работы знания имеют большое значение для дальнейшего освоения дисциплины и могут найти практическое применение в будущей профессии.
2 Задание
Для электрических цепей, схемы которых изображены на рисунке 1, по заданным величинам сопротивлений и ЭДС (таблица А1) выполнить следующее:
1 Составить систему уравнений, необходимых для определения токов по первому и второму законам (правилам) Кирхгофа (для всех узлов и независимых контуров, без расчета);
2 Рассчитать токи во всех ветвях заданной схемы методом контурных токов;
3 Составить баланс мощностей;
4 Рассчитать потенциалы всех точек и напряжения на элементах (резисторы и источники напряжения);
5 Построение потенциальной диаграммы одного замкнутого контура, содержащего как минимум два источника ЭДС;
6 Провести моделирование схемы в программе схемотехнического моделирования;
7 Разработать программу в пакете MathCad;
8 Рассчитать относительную погрешности токов и напряжений при расчете (п. 2) и моделировании (п.6);
Дополнительное задание:
9 Выполнить расчет схемы методом наложения.
Таблица 1 – Параметры элементов схемы
| № вар. | R1, Ом | R2, Ом | R3, Ом | R4, Ом | R5, Ом | R6, Ом | Е1, В | Е2, В | Е3, В |
| 39 | 30 | 12 | 10 | 85 | 15 | 50 | 50 | 150 | 120 |
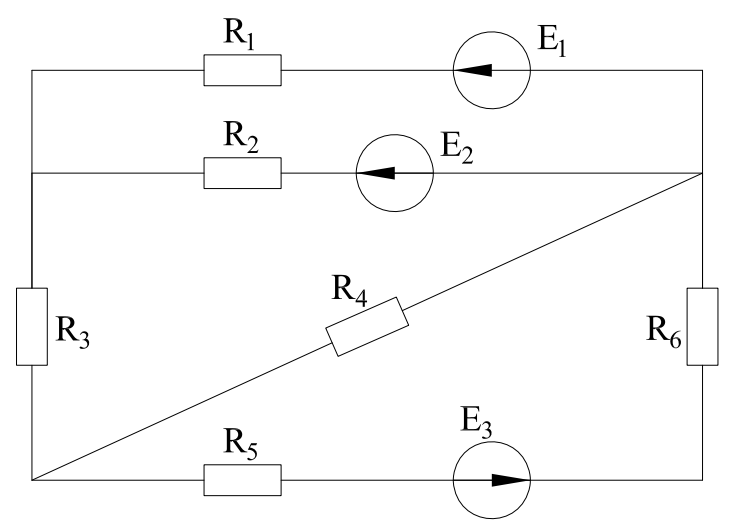
Рисунок 1 – Схема задачи
3 Теоретический расчет
3.1 Составление системы уравнений по первому и второму законам (правилам) Кирхгофа или метод непосредственного применения законов Кирхгофа
Метод непосредственного применения законов Кирхгофа применяется для расчета сложных цепей постоянного и переменного тока [1].
В общем случае искомые токи (напряжения) ветвей находятся по результатам решения системы уравнений, которые составляются по первому и второму законам Кирхгофа.
Перед составлением уравнений необходимо провести топологический анализ схемы – определить число узлов, ветвей, независимых контуров в схеме
Ветвь (В) – участок электрической цепи, элементы в которой соединены последовательно и по которой протекает один и тот же электрический ток.
Узел (У) – место соединения не менее трех ветвей электрической цепи (место, где соединены две ветви, называется не узлом, а соединением).
Контур (к) – последовательность ветвей электрической цепи, образующая замкнутый путь, в которой один из узлов одновременно является началом и концом пути, а остальные встречаются только один раз. Разновидностью контуров в электрической цепи обособленно выделяют независимые контура (кН), которые отличаются друг от друга наличием хотя бы одной ветви не входящие в другие контура.
Для любой схемы минимальное число независимых контуров зависит от числа ветвей и числа узлов в цепи и можно определить по формуле:
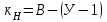 . (1)
. (1)Для схемы на рисунке 2 принимаем следующее:
а) пять ветвей (бвг, аж, де, икл, мнпр);
б) три узла (1, 2, 3);
в) три независимых контура (I - абвгдеж, II – аиклмнпрж, III - мнпред).
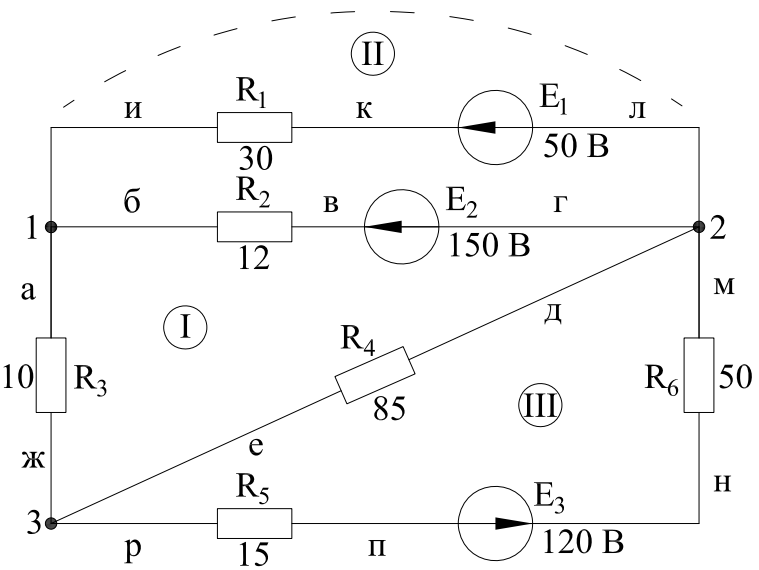
Рисунок 2 – Схема задачи с указанием ветвей, узлов и контуров
Выбираем, условно, положительные направления токов в ветвях и обозначаем их на схеме пунктирными линиями (рисунок 3).
Выбираем положительные направления обхода (НО) трех независимых контуров. Нумеруем НО в соответствии с выбранными контурами и указываем стрелками направления (рисунок 3).
Составляем систему уравнений по I закону Кирхгофа.
Количество уравнений по I закону Кирхгофа n определяется по формуле:
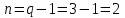 , (2)
, (2)где q – число узлов в схеме.
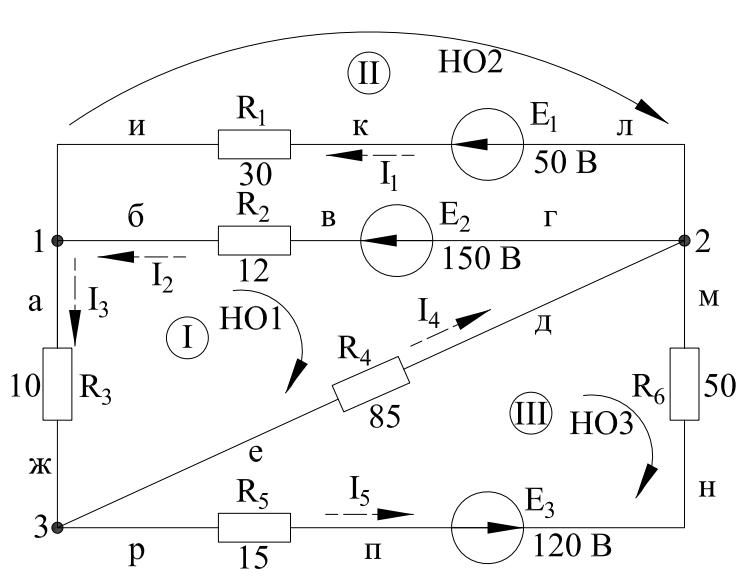
Рисунок 3 – Схема с обозначением НО и токов
Формулировка I закона Кирхгофа: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Или: алгебраическая сумма всех токов в узле равна нулю [2].
Уравнение по I закону Кирхгофа для узла 1 имеет следующий вид:
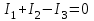 . (3)
. (3)Уравнение по I закону Кирхгофа для узла 2 имеет следующий вид:
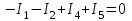 . (4)
. (4)Уравнение по I закону Кирхгофа для узла 3 имеет следующий вид:
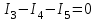 . (5)
. (5)Составим недостающие уравнения по II закону Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «–». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «–»;
– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «–».
Т.к. общие количество уравнений в системе равно числу неизвестных токов в цепи (для нашей задачи пять неизвестных токов), то по второму закону Кирхгофа составляем три недостающих уравнения для трех независимых контуров.
Уравнение по II закону Кирхгофа для НО1 имеет следующий вид:
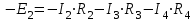
. (6)
Уравнение по II закону Кирхгофа для НО2 имеет следующий вид:
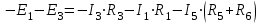 . (7)
. (7)Уравнение по II закону Кирхгофа для НО3 имеет следующий вид:
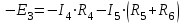 . (8)
. (8)Из формул (3) – (8) составляем систему уравнений:
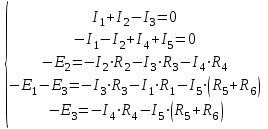 . (9)
. (9)3.2 Расчет схемы методом контурных токов
В методе контурных токов, вместо токов ветвей по второму закону Кирхгофа формируют так называемые контурные токи, замыкающиеся в контурах. Контурный ток – условный ток, имеющий одинаковое значение на всех участках выбранного независимого контура. Составив уравнения и решив ее любым способом, можно перейти от контурных токов к токам ветвей на основании простых соотношений.
Минимально необходимое число уравнений для расчета схемы по методу контурных токов равно числу минимальному числу независимых контуров кН (формула 1), но не менее двух.
Для решения схемы, приведенной в примере достаточно составления всего двух уравнений, по двум независимым контуров, но при этом можно составить и три уравнения. Для учебных целей составим три уравнения по трем независимым контурах.
Выбираем контура абвгдеж, иклгвб, мнпред.
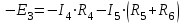 . (10)
. (10)В этом выражении использованы следующие обозначения:
Равные индексы, относящиеся к сопротивлению, представляют собой суммарную величину для k-го контура электрической цепи.
Если для сопротивления использованы индексы k и m, то речь идёт об общем сопротивлении, которое входит одновременно в 2 контура с такими номерами.
Нужно обратить внимание, что в последней формуле присутствуют контурные токи в k-м контуре.
С правой стороны знака равенства указана суммарная электродвижущая сила для k-го контура.
При определении неизвестной величины слагаемое берётся с плюсом в тех ситуациях, когда направления электротоков в соседних контурах совпадают, и с минусом, когда они противоположные. ЭДС контура может быть положительной или отрицательной. Первый вариант применяется в тех случаях, когда направления электродвижущей силы и контурного электротока совпадают. В противном случае ЭДС берётся с минусом.
| | | | | | ЛР 2068999-43-39-ПЗ |
| |||
| | | | | | |||||
| Изм. | Лист | № докум. | Подп. | Дата | |||||
| Подп. и дата | | ||||||||
| Инв. № дубл. | | ||||||||
| Взам. инв. № | | ||||||||
| Подп. и дата | | ||||||||
| Инв. № подл. | | ||||||||
| | | Формат А4 |