Файл: Эксплуатация транспортнотехнологических машин и комплексов.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 10

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
Институт машиностроения

(наименование института полностью)

Эксплуатация транспортно-технологических машин_и комплексов.

(наименование учебного структурного подразделения)

Автомобили и автомобильный сервис

(код и наименование направления подготовки / специальности)




(направленность (профиль) / специализация)



Практическое задание №6
по учебному курсу «Высшая математика 3»

(наименование учебного курса)
Вариант 5 (при наличии)



Студент
Соколиков Александр Тимурович






(И.О. Фамилия)



Группа
ЭТКбд-1902бс












Преподаватель

Палфёрова Сабина Шехшанатовна






(И.О. Фамилия)



Тольятти 2023

Задача 1 (формулировка полностью): Найти модуль и главное значение аргумента комплексных чисел, записать это число в тригонометрической и показательной формах.



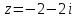
Решение:

Найдем модуль заданного комплексного числа: .

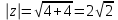Найдем главное значение аргумент заданного комплексного числа:

.

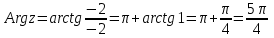В тригонометрической форме имеем: .

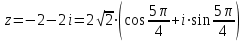В показательной форме имеем: .

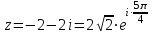Ответ: смотреть выше.

Задача 2 (формулировка полностью): Вычислить

а)

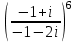
б)

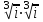
Решение:
а)

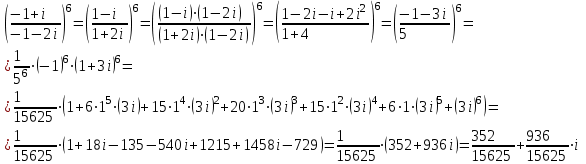
б) .

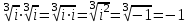Ответ: а) 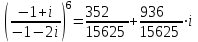; б) .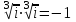

Задача 3 (формулировка полностью): Найдите значение действительной и мнимой частей функции.



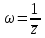
Решение:

Комплексное число равно 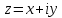, сопряженное к нему 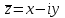, тогда

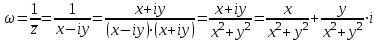, следовательно,

действительная часть 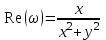и мнимая часть .

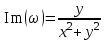Ответ: , .
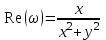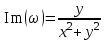Задача 4 (формулировка полностью): Дана функция 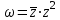. Найти значение функции при заданном значении z.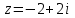



Решение:

Комплексное число равно 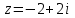, сопряженное к нему 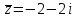, тогда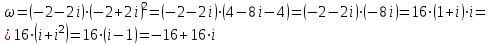



Ответ:
.
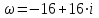
Задача 5 (формулировка полностью): Найти Ln z, .

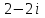Решение:

Представим заданное комплексное число в показательной форме:

Найдем модуль заданного комплексного числа: .

Найдем главное значение аргумент заданного комплексного числа:

.

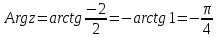В показательной форме имеем: 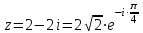. Вычислим :

.

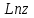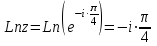Ответ: .

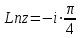Задача 6 (формулировка полностью): Пользуясь условиями Коши – Римана, выяснить, является ли функция 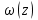дифференцируемой хотя бы в одной точке.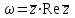



Решение:

Представим функцию 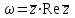в виде 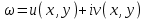. Для этого подставим в функцию и выделим действительную и мнимуючасти: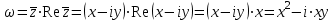


Таким образом, действительная часть функции 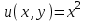, а ее мнимая часть .
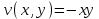Функция является аналитической, если она дифференцируема, то есть удовлетворяет условиям Коши-Римана:



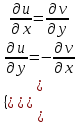
Проверим функцию 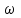на аналитичность:

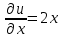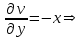
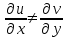
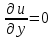и

и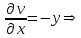
.

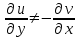
Так как условия Коши-Римана не выполняются, функция не является аналитической. Условия Коши-Римана будут выполняться лишь в точке .

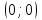Ответ: функция во всех точках не дифференцируема, кроме точки .

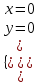Смотрите также файлы