ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 79
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 1.
Алгоритм нахождения простого числа.
Требуется составить алгоритм (в виде блок-схемы), который бы определял, является ли заданное число простым или нет.
Допустим, входными данными будет число N. Как определить, является ли оно простым или нет?
1 вариант: можно последовательно делить N на числа в интервале от 2 до N-1, если при делении N на какое-либо из этих чисел остатка не остается, то число не является простым, если же все числа перебраны, а остаток от деления остается, значит, число является простым. Является ли алгоритм эффективным? Почему?
Алгоритм, который последовательно делит число N на числа в интервале от 2 до N-1, является простым, но не самым эффективным способом определения простоты числа. Его сложность составляет O(N), так как в худшем случае нужно выполнить N-1 деления. Этот подход будет работать для небольших чисел, но для больших чисел он становится слишком медленным.
2 вариант: можно последовательно делить N на числа в интервале от 2 до N/2. При делении числа N на числа от N/2+1 до N-1 результат будет варьироваться в диапазоне от 1.999 до 1.001, что явно дает остаток, а, значит, не удовлетворяет нашим условиям. Можно ли улучшить данный алгоритм?
Алгоритм, который последовательно делит число N на числа в интервале от 2 до N/2, является оптимизацией предыдущего подхода. Так как делители больше N/2 не могут давать целочисленного результата, можно ограничиться проверкой только до N/2. Это сокращает количество делений, но сложность все равно составляет O(N), что делает его недостаточно эффективным для больших чисел. Данный подход можно улучшить следующим вариантом, ещё больше сократив количество делений.
3 вариант: если мы последовательно перебираем делители числа N, то сам делитель будет увеличиваться, а результат деления при увеличении делителя - уменьшаться. Это будет наблюдаться до некоторого числа h, при котором и делитель и результат деления будут равны. При увеличении делителя больше числа h делитель будет увеличиваться в тому же диапазоне, в котором ранее уменьшался результат деления. Чему равно число h? Какой тогда будет оптимизированный интервал увеличения делителя?
Данный подход предлагает оптимизировать алгоритм, ограничив проверку делителей числа N только до квадратного корня из N. Действительно, если число N имеет
делитель больше его квадратного корня, то обязательно будет иметь и делитель меньше него. Это позволяет сократить количество делений, что улучшает эффективность алгоритма.
Чтобы найти число h, при котором делитель и результат деления равны, можно представить N в виде произведения двух чисел: h и q, где h <= q. Тогда при увеличении h, q будет уменьшаться, и наоборот. При этом, если оба числа равны, то они должны быть равны квадратному корню из N. Таким образом, число h будет равно квадратному корню из N.
Оптимизированный интервал увеличения делителя будет от 2 до
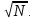Если в этом интервале не найдено делителей, то число N является простым. Это позволяет существенно уменьшить количество делений и значительно улучшить эффективность алгоритма для больших чисел.Блок-схема последнего варианта алгоритма представлена ниже:
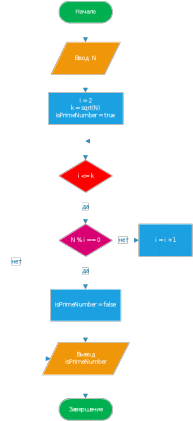
Задание 2
Составить алгоритм (в виде блок-схемы) который бы считал количество чисел в разных диапазонах.
Допустим, у нас есть 4 диапазона чисел 1-25, 26-50, 51-75, 76-100. Как подсчитать количество простых чисел содержащихся в каждом из этих диапазонов?
С первым диапазоном сложностей не возникает. Создаем счетчик. Проверяем последовательно каждое число диапазона, если оно простое прибавляем к счетчику единицу. Но как реализовать алгоритм со вторым и последующими диапазонами?
1 вариант: на примере второго диапазона. Создаем счетчик. Проверяем последовательно каждое число от 1 до верхней границы второго диапазона, если оно простое прибавляем к счетчику единицу. Затем из значения счетчика вычитаем количество предыдущего (первого) диапазона. В чем будут заключаться отрицательные стороны работы алгоритма?
Отрицательные стороны алгоритма в первом варианте заключаются в том, что для подсчёта количества простых чисел в текущем диапазоне необходимо каждый раз считать количество простых чисел во всех предыдущих диапазонах. Временная сложность в таком случае практически равна
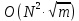, где N – общее количество чисел в диапазонах
, а m – количество чисел в диапазоне от 2 до текущего числа, так как внутри перебора мы так же осуществляем проверку на то, что число простое, а она выполняется за
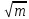в лучшем варианте из задания 1.2 вариант: можно последовательно перебирать только числа данного диапазона. Это ускорит работу алгоритма, но вместе с тем усложнит его.
Сравнить во сколько второй вариант алгоритма работает быстрее чем первый, для каждого из четырех диапазонов.
Для каждого из диапазонов второй алгоритм работает быстрее в N раз, так как не нужно выполнять перебор предыдущих диапазонов.
Блок-схема последнего варианта алгоритма представлена ниже:
