Файл: Предмет, задачи и организационноправовые основы огневой подготовки. Меры безопасности при обращении с оружием и боеприпасами.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 1133
Скачиваний: 18
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тем не менее, через некоторое время канал ствола оказывался пораженным коррозией. Причиной этого является рассмотренное выше действие растворимых солей нагара от капсюльного состава.
В последние годы правила чистки оружия, изложенные в наставлениях по стрелковому делу, основываются на положениях новой теории коррозии оружия, разработанной В.Н.Поддубным.
| Правила чистки оружиязаключаются в следующем: ∙ оружие необходимо чистить немедленно после стрельбы, по возможности на самом стрельбище; ∙ весь нагар необходимо удалять при первой же чистке; ∙ оружие следует чистить вторично для удаления нагара, который мог остаться в стволе, если первая чистка производилась в недостаточно удобных условиях (на стрельбище). Вторичная чистка производится немедленно по приходу в места постоянной дислокации; ∙ для стрелкового оружия, если ствол отпотел при внесении его после стрельбы с холода в тёплое помещение, чистка производится немедленно, чтобы не дать оружию согреться, а капелькам росы высохнуть; ∙ после чистки ствол протирается насухо и затем слегка смазывается. |
При правильном уходе за стволом можно избежать ржавления и, следовательно, образования сыпи и раковин. Правильный уход за оружием позволяет значительно повысить срок службы ствола.
Живучесть стволов стрелкового оружия достигает 10 - 12 тысяч выстрелов, а хромированного - до 30 тысяч выстрелов.
Отсюда становится понятной важность строгого соблюдения режима огня, своевременной смены нагретых стволов и учёта по формулярам общего числа выстрелов.
Стволы крупнокалиберных пулеметов, где при выстреле Pm достигает 3050 кг/см2 имеют меньшую живучесть. Так, у 14,5-мм крупнокалиберного пулемета после 1000 выстрелов начальная скорость падает.
Начальная скорость снаряда
| Начальная скорость снаряда (V0) -это условная скорость в точке вылета, которая получается расчётным путём |
Начальная скорость является одной из важнейших баллистических характеристик оружия, оказывающей влияние на его боевые свойства.
При увеличении начальной скорости увеличиваются дальность полёта снаряда, настильность траектории, поражаемое пространство, бронепробиваемость, а также уменьшается влияние внешних условий на полёт снаряда.
В таблицах стрельбы и наставлениях указываются величины начальных скоростей несколько большие, чем скорость снаряда в момент вылета (Vд).
Объясняется это следующим образом. При движении снаряда по каналу ствола под действием пороховых газов скорость его все время увеличивается и достигает значения Vд.
Если бы период последействия отсутствовал, то эта скорость была бы наибольшей, ею определялось бы начало движения снаряда в воздухе.
Но во время периода последействия под давлением истекающих газов скорость снаряда продолжает ещё несколько увеличиваться и достигает какого-то значения Vm (рис. 12), после которого начинает убывать.
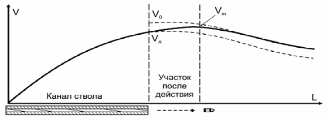
| Рис. 12. Выбор начальной скорости |
Участок периода последействия газов у оружия незначителен, поэтому считают, что снаряд после вылета из канала ствола не подвергается действию пороховых газов.
Но в этом случае действительная скорость снаряда в момент вылета оказывается не связанной с кривой изменения скорости полёта снаряда в воздухе.
Для того, чтобы избежать такого разрыва, за начальную скорость принимается такая условная скорость в точке вылета, которая согласовывается с кривой скоростей снаряда за пределами участка последействия.
Таким образом, начальная скорость определяется по закономерностям, характеризующим изменение скорости снаряда в воздухе. Следовательно, для определения начальной скорости необходимо определить скорость снаряда в определённых точках в воздухе и затем полученную кривую построить до дульного среза.
Для определения скорости снаряда в какой-либо точке в воздухе применяются специальные приборы - хронографы*.
Сущность определения скорости снаряда при помощи хронографа заключается в следующем (рис. 13).
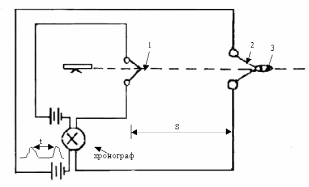
| Рис. 13. Принципиальная схема измерителя скорости. S - расстояние между мембранами; t - время между импульсами; 1 - первая мембрана; 2 - вторая мембрана; 3 - пуля. |
На опредёленном расстоянии друг от друга устанавливаются две мишени, которые представляют собой либо деревянную раму с натянутой проволокой (для артиллерийских систем), либо наклеенную на бумагу фольговую мишень (поз. 1 и 2) (для стрелкового оружия), рассчитанную так, чтобы снаряд (поз. 3) обязательно при пробивании рамы перервал проволоку или фольговую полоску.
При этом разъединяется электрическая цепь. Обе рамы-мишени соединены с хронографом. При пробивании снарядом поочерёдно первой и второй рам-мишеней хронограф даёт возможность определить время полёта снаряда между двумя рамами.
Зная расстояние между рамами-мишенями и принимая движение на этом участке равномерным, определяют среднюю скорость снаряда на участке между рамами-мишенями по формуле:
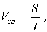
| где Vср - средняя скорость снаряда на участке между двумя рамами- мишенями; S - расстояние между рамами-мишенями; t - время полета снаряда между рамами-мишенями. |
Обычно расстояние между рамами-мишенями составляет 50 м, поэтому найденную среднюю скорость Vср. принимают за скорость снаряда в 25 м от дульного среза (V25).
*Хронографами называются приборы, при помощи которых измеряется время движения снаряда с целью определения его скорости.
Прицеливание
Под прицеливанием понимают совмещение на одной линии глаза стрелка, прорези прицела, мушки и точки прицеливания. Понятие ровной мушки в прорези подразумевает положение их верхних срезов на одной линии и равенство просветов между боковыми гранями мушки и прорези целика, при этом линия прицеливания проходит через середину верхнего среза мушки.
Необходимо отметить, что идеальную картину прицеливания можно рассматривать лишь теоретически, когда видны четко и мушка в прорези и точка прицеливания, а элементы прицельного приспособления не имеют колебаний. Реально дело обстоит далеко не так.
Стрелок наблюдает, как все оружие хаотически "гуляет" по мишени, а мушка при этом "скачет" в прорези целика. И все колебания увеличиваются с началом нажатия на спусковой крючок. При малом опыте стрельбы из-за такой тряски перед глазами, возникает естественное желание "поймать десятку" и нажать на спуск в наиболее выгодном положении оружия на цели. Результатом будет... далекий отрыв.
Но так ли страшны колебания оружия? Оружие, удерживаемое человеком, всегда будет иметь некоторые колебания, обусловленные рядом физиологических причин. Невозможно добиться идеальной устойчивости, при которой оружие будет абсолютно неподвижно.
При стрельбе с одной руки возникают два основных вида колебаний:
-
Колебания всей руки относительно плечевого сустава (точка Б, рис.4), при которых все оружие "гуляет" относительно мишени; -
Колебания в лучезапястном (кистевом) суставе (точка А, рис.4), при которых визуально наблюдаются колебания мушки в прорези.
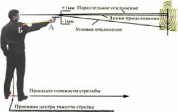
Рис.4. Угловые и параллельные колебания оружия
Кроме того имеются малозначительные колебания в локтевом суставе и в пояснице, а также качания всего тела относительно пола. То есть получается многозвеньевая система ограниченной устойчивости с множеством степеней свободы, амплитуда колебаний которой зависит от натренированности стрелка и, как правило, увеличивается при нажиме на спусковой крючок или при возникновении стрессовых ситуаций.
Рассмотрим с помощью математики влияние колебаний на точность стрельбы, для чего сначала проведем следующий эксперимент. Прикрепим к стене линейку на уровне глаз. Удерживая пистолет на вытянутой руке в сантиметре от линейки, посмотрим, в пределах скольки миллиметров колеблется мушка по вертикали и по горизонтали. Даже у самого неопытного стрелка эти колебания не будут превышать 3 мм.
После замера своих колебаний можно рассчитать перемещение точки прицеливания на дальности 25 м, исходя из пропорций в соответствии с рис.5.
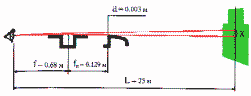
Рис. 5. Параллельные колебания пистолета
a/c = (f + fп)/L (6)
После преобразования получим:
c = a [L/(f + fп)] = 0,03 * [25/(0,68+0,129)] = 9.3 см (7)
Полученный результат красноречиво говорит о том, что при колебаниях оружия в пределах 3 мм при ровной мушке в прорези точка попадания на дальности 25 м при стрельбе по мишени № 4 (грудная фигура с кругами) не выходит из "десятки", диаметр которой равен 10 см. А при колебаниях мушки в пределах 1 мм смещение центров пробоин составит максимум 3,1 см.
Теперь рассмотрим колебания оружия в половину мишени от нижнего среза до центра (рис.6), что соответствует перемещению мушки в пределах 8 мм (размер "а", рис.5), величину которых можно рассчитать в соответствии с выражением (6):
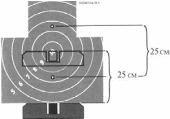
Рис.6. Результат колебания оружия в половину мишени
a = c [(f + fп)/L] = 0,25 [(0,68 + 0,129)/25] = 0,00809 м = 8,1 мм
Из рис. 6 видно, что при колебаниях пистолета в половину мишени пуля будет иметь максимальные отклонения до середины "восьмерки", т.е. при трех выстрелах результат должен быть не менее 24 очков. Но учитывая подчинение рассеивания пуль нормальному закону распределения (вероятность попадания ближе к центру больше), мы получаем даже при таких небывало больших колебаниях оружия (в половину мишени) результат не менее 25 очков, что является отличной оценкой при выполнении 1го упражнения учебных стрельб из пистолета Макарова.
Таким образом, колебания оружия относительно плечевого сустава с достоаточной точностью можно считать параллельными и особого влияния на точность стрельбы не оказывающими.
Второй вид колебаний, оказывающий основное влияние на рассеивание пуль, это угловые колебания оружия, которые происходят в лучезапястном (кистевом) суставе (точка А, рис.4). Определим возможные отклонения пробоин для пистолета ИЖ-71 при стрельбе на 25 м при таких колебаниях, принимая, что параллельные колебания отсутствуют.
Возьмем крайний случай, когда выбран полностью боковой зазор в прицельном приспособлении, т.е. мушка "прижата" к целику (Рис.7).
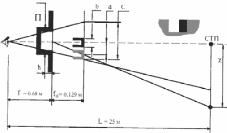
Рис. 7. Смещение СТП при "прижатой" мушке к целику
Кроющую величину прорези прицела на плоскости мушки находим из подобия треугольников: