Файл: Отчет по Расчетнографической работе по дисциплине Неирокомпьютерные технологии.docx
Добавлен: 08.11.2023
Просмотров: 10
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное
учреждение высшего образования
«Севастопольский государственный университет»
Петраков Василий Александрович
Институт информационных технологий и управления в технических системах
курс 1 группа ИС/м-11-о
09.04.02 Информационные системы и технологии (уровень магистра)
ОТЧЕТ
по Расчетно-графической работе
по дисциплине «Нейрокомпьютерные технологии»
на тему «Аппроксимация функций RBF нейронными сетями»
Отметка о зачете ____________________ ________
(дата)
Руководитель практикума
доцент Бондарев В.Н.
(должность) (подпись) (инициалы, фамилия)
Севастополь 2019
1 Цель работы
Изучение архитектуры RBF сетей, формирование умений в области расчетов параметров RBF-сетей, приобретение навыков самостоятельного решения прикладной задачи с помощью нейросетей.
2 Вариант задания и алгоритм работы
Требуется выполнить с помощью RBF-cети со структурой 1-S-1 аппроксимацию одномерной функции f(x), номер которой соответствует варианту задания и которая задана в N точках, равномерно распределенных на отрезке:
Для выполнения данной расчетной работы были произведены действия по данному алгоритму:
1) определить на языке Scilab заданную функцию и построить её график (см. рисунок 1);
2) изобразить архитектуру сети при S=N;
3) подготовить обучающее множество с числом элементов, равным N;
4) выбрать значения весов первого слоя в соответствии с входными данными;
5) определить смещения первого слоя, обеспечив адекватное перекрытие базисных гауссовых функций;
6) выполнить вычисление весов и смещений второго слоя в соответствии с алгоритмом LS, используя систему Scilab.
7) выполнить моделирование RBF сети при вычисленных значениях параметров. Для этого определить соответствующую функцию на языке Scilab, назвав её ann_rbf_run.
8) сравнить значения функции, вычисляемые по заданной формуле и с помощью модели RBF-сети как в заданных точках N, так и в тех точках, которые не использовались для обучения. Для этого построить соответствующие графики.
9) вычислить среднюю относительную ошибку аппроксимации функции с помощью модели RBF-сети.
10) подготовить отчет по работе в соответствии с пунктами выполнения, указанными выше, защитить отчет.
3 ХОД РАБОТЫ
Архитектура RBF сети, используемая в данной работе представлена на рисунке 1.
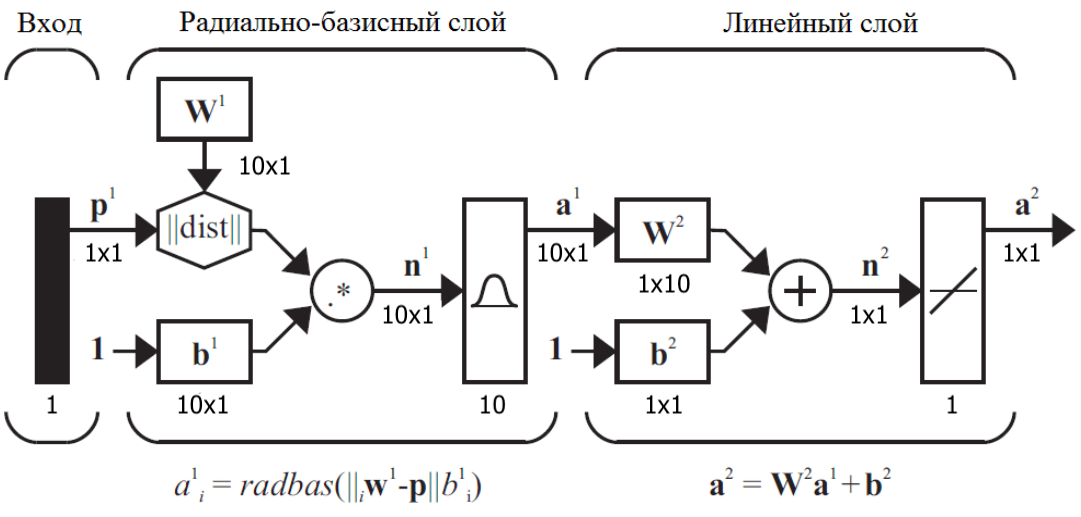
Рисунок 1 – Архитектура RBF сети
Произведена кластеризация входного пространства и выбор центров кластеров в качестве центров базисных функций для настройки центров и смещений нелинейного первого слоя благодаря чему центры базисных функций размещаются в областях входного пространства со значительной активностью.
Обучение линейного слоя происходило на основе алгоритма LS.
В ходе выполнения работы были получены результаты, представленные на рисунках 2-8.
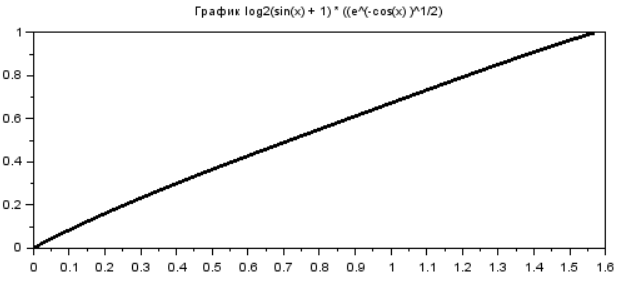
Рисунок 2 – График функции
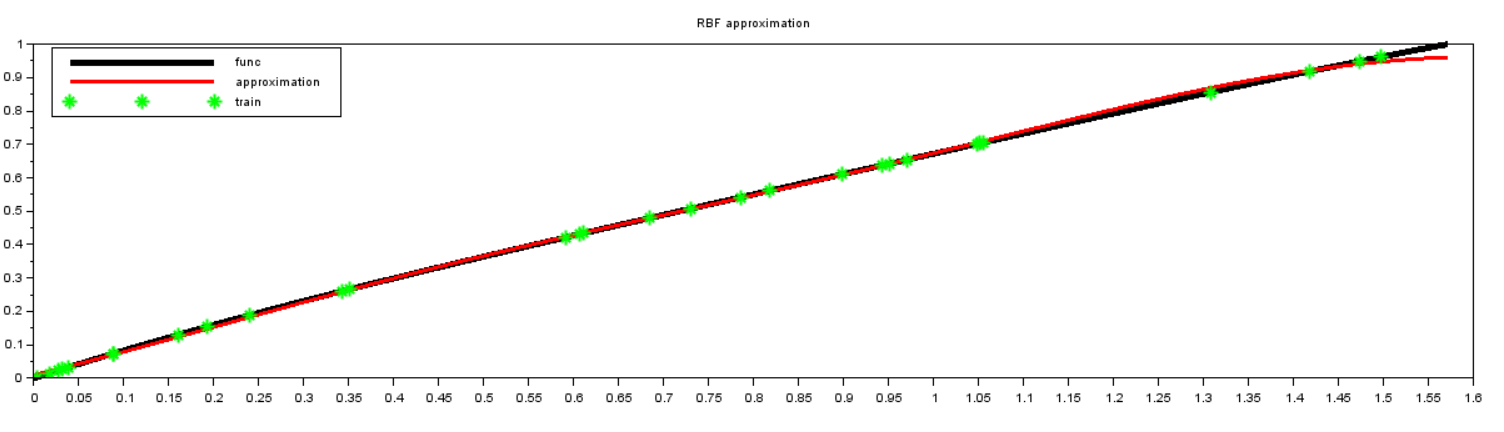
Рисунок 3 – Тренировка
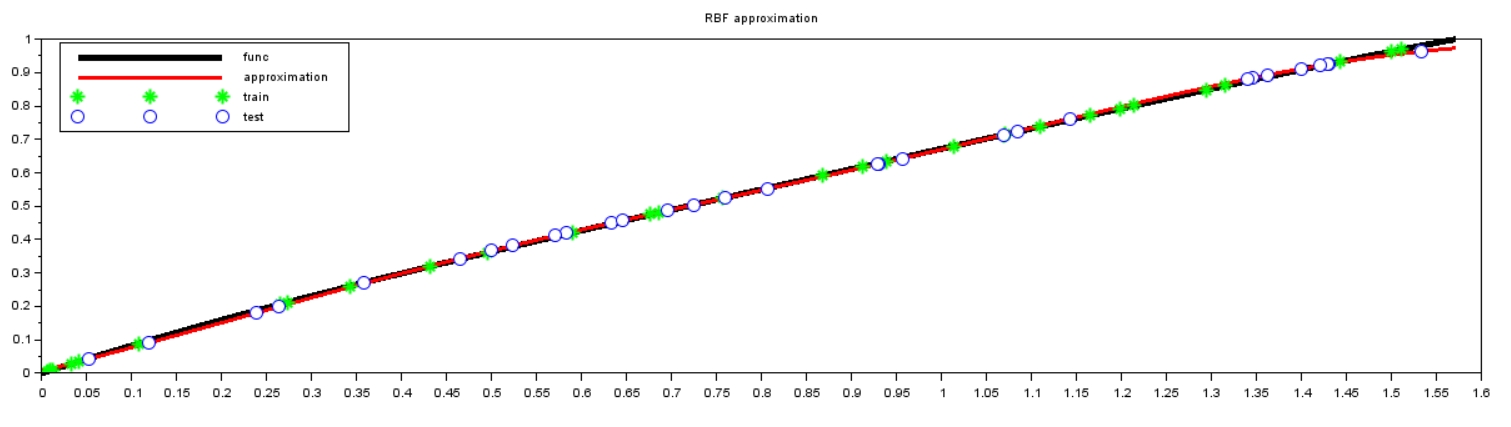
Рисунок 4 – Тест
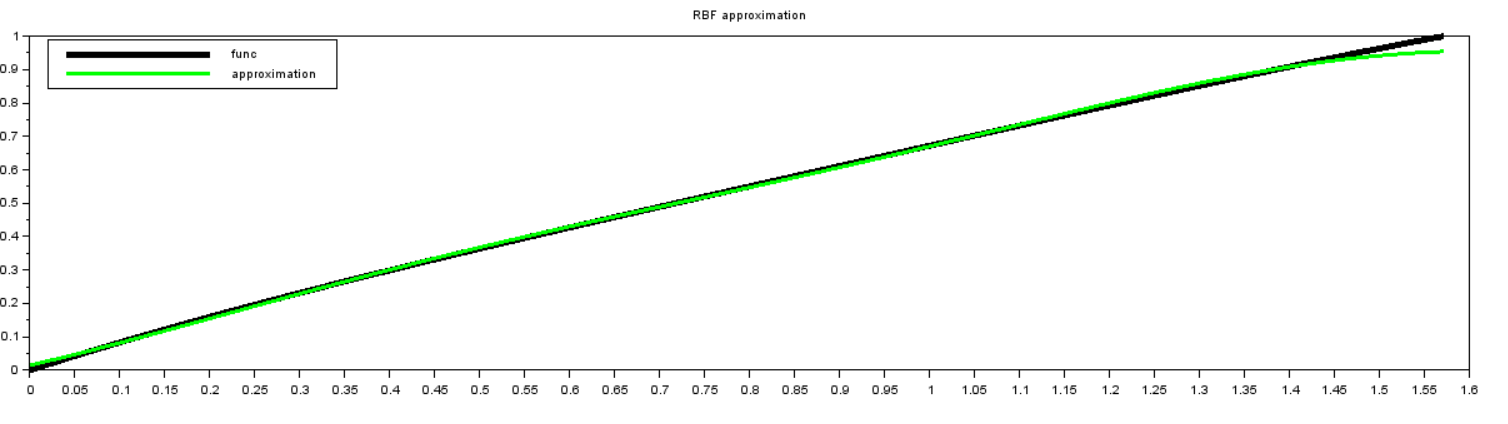
Рисунок 5 - Аппроксимация
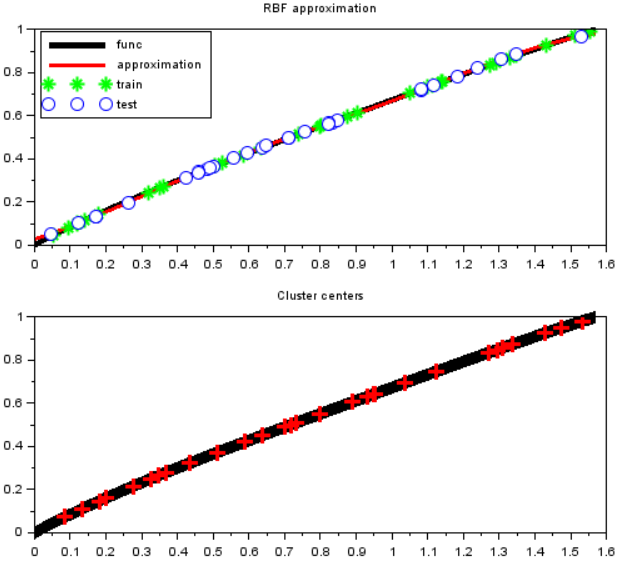
Рисунок 6 – Сводные результаты и центры кластеров
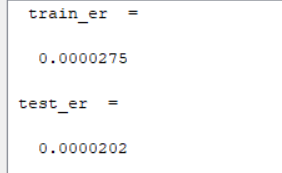
Рисунок 7 – Ошибки при обучении и тестировании
Можно заметить, что переобучения не произошло, т.к. ошибка при тестировании меньше чем при обучении. Ошибка при обучении равна 0.0000275, а при тестировании – 0.0000202 (см. рис. 7).
Веса и смещения представлены на рисунке 8.

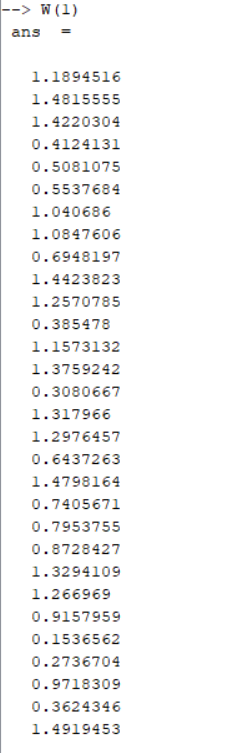
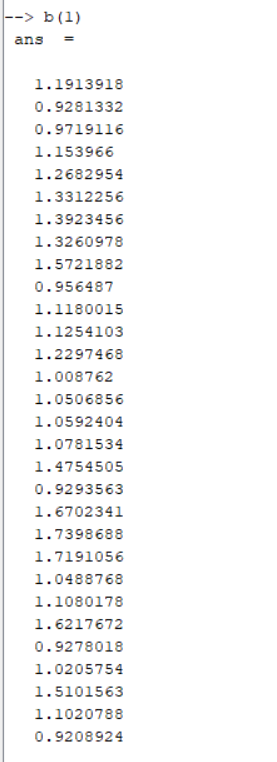

Рисунок 8 – Веса и смещения
ВЫВОДЫ
В результате выполнения лабораторной работы была изучена архитектура RBF сетей, сформированы умения в области расчетов параметров RBF-сетей, приобретены навыки самостоятельного решения прикладной задачи с помощью нейросетей. Можно подтвердить, что результат апроксимации в сильно зависит от выбора весов первого слоя, а, следовательно, от распределения векторов входных данных. Это было подтверждено многократным прогоном модели сети (различной инициализации векторов весов)
ПРИЛОЖЕНИЕ А
| | clear; xdel(winsid()); clc; mode(2); xmin = 0; xmax = %pi/2; N = 30; function y=f(x) y = log2(sin(x) + 1).*(((%e).^(-cos(x))).^0.5); endfunction function y=ann_RBF_run(P, W, b) a1 = ann_radial_basis_func_run(P, W(1), b(1)); a2 = ann_ADALINE_run(a1, W(2), b(2)); y = a2; endfunction function y=ann_radial_basis_func_run(P, w, b) d = ann_dist(w, P); b = repmat(b, 1, size(d,2)); n = d .* b; y = ann_radbas_activ(n); endfunction function y=ann_radbas_activ(x) y = exp(-x .* x); endfunction function [W, b]=ann_RBF(P, T, N2, lr, itermax, nc, ro) rhs=argn(2); if rhs < 3; error("Expect at least 3 arguments, P,T and N2");end if rhs < 4; lr = 0.01; end if rhs < 5; itermax = 100; end if rhs < 6; nc = floor(length(P) / N2); end if rhs < 7; ro = 0.01; end if lr == []; lr = 0.01; end if itermax == []; itermax = 100; end if nc == []; nc = floor(length(P) / N2); end if ro == []; ro = 0.001; end // Матрицавесов [N1,col1]=size(P); N=[N1,N2,1]; W = list(); b = list(); W(1) = grand(N1, N2, 'unf', min(P), max(P))'; function w=center_by_clustering() w = W(1); for itercnt = 1:itermax for Pcnt = 1:size(P,2) most_close = ann_COMPET_run(w, P(Pcnt)); update_neuron = find(most_close); w(update_neuron) = w(update_neuron) + lr*(P(Pcnt) - w(update_neuron)); end end endfunction function b2=biases() dist = ann_dist(W(1),P); dist = gsort(dist, 'c', 'd'); dist = dist(1:$, 1:nc); dist = (sum(dist.^2, 2) .^ 0.5) ./ nc; b2 = 1 ./ (sqrt(2) .* dist); endfunction W(1) = center_by_clustering(); b(1) = biases(); function [W, b]=LS() a1 = ann_radial_basis_func_run(P, W(1), b(1)); z = a1; z($+1, 1:$) = 1; t = T'; U = z'; I = eye(size(U, 2), size(U, 2)); x_star = inv(U'*U + ro*I) * U' * t W = x_star(1:$-1)'; b = x_star($)'; endfunction [W2, b2] = LS(); W(2) = W2; b(2) = b2; endfunction Q = 2*N; x = grand(1,Q,'unf',xmin,xmax); x_train = x(1:N); T_train = f(x_train); x_test = x(N+1:$); T_test = f(x_test); [W, b] = ann_RBF(x_train,T_train,N, [],[],3); y_train = ann_RBF_run(x_train, W, b); e_train = y_train - T_train; train_er = mean(e_train .^ 2) y_test = ann_RBF_run(x_test, W, b); e_test = y_test - T_test; test_er = mean(e_test .^ 2) x = linspace(xmin, xmax, 100); y = f(x); y2 = ann_RBF_run(x, W, b); figure; clf(); gcf().background = 35; subplot(2,1,1); plot(x,y, 'k', 'linewidth', 5); plot2d(x,y2,style=color('red')); p = gca().children(1).children(1); p.thickness = 3; plot(x_train, T_train, 'g*', 'MarkerSize', 10, 'linewidth',2); plot(x_test, y_test, 'bo', 'MarkerSize', 10, 'linewidth',1); legend(['func', 'approximation', 'train', 'test'], "in_upper_left"); title('RBF approximation') subplot(2,1,2); plot(x,y, 'k', 'linewidth', 10); center_y = f(W(1)); plot(W(1), center_y, 'r+', 'MarkerSize', 10, 'linewidth', 3); title('Cluster centers') |