Файл: .docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 18

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.



Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления
Форма обучения: заочная






ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

СТАТИСТИКА




Группа Ом20М611

Студент



Николай Александрович Копосов
















МОСКВА 2021

Раздел Общая теория статистики


Тема Абсолютные и относительные величины
По данным таблицы рассчитать поквартально проценты установленного планового задания и проценты выполнения плана по выпуску продукции; Расчетные данные оформить в таблице.


Кварталы
Выпуск продукции, млн. руб.

Процент выполнения плана

Процент планового задания

Базисный

период
Отчетный период

план

факт

I
22,25
22,28

24,15

108,4
100,1

II
21,30
21,35

23,62

110,6
100,2

III
22,30
22,94

23,93

104,3
102,7

IV
22,20
22,29

24,08

108,0
100,4



Решение:

Относительная величина планового задания (показатель планового задания) представляет собой отношение планируемого уровня показателя к его уровню, достигнутому в предыдущем периоде (или в периоде, рассматриваемом как базисный).

ОВПЗ=упл/у0·100%,

Рассчитываем процент выполнения плана:

24,15/22,28*100= 108,4

23,62/21,35*100=110,6

23,93/22,94*100=104,3

24,08/22,29*100=108,0
Рассчитываем планового задания

ОВПЗ = плановый уровень на будущий (следующий) период / фактический уровень текущего (предыдущего) периода
22,28/22,25*100=100,1

21,35/21,30*100=100,2

22,94/22,30*100=102,7

22,29/22,20*100=100,4
Тема Средние величины
По данным таблицы рассчитать средний стаж работника

Группы работников по общему стажу работы, лет
Численность
работников, чел. (m)

до 5
18

5-10
40

10-15
15

свыше 15
10







Итого
83



Решение:

Признаком в данной задаче является общий стаж рабочего, а частотами соответственно количество рабочих, имеющих тот или иной стаж. Ряд распределения - интервальный, причем первый и последний интервал - открытые.
Если интервалы открыты, то по правилам принимаем величину первого интервала равной второму, а последнего предпоследнему. Так как имеются и значения признака и частоты, то средний стаж находим по формуле средней арифметической взвешенной. А так как ряд интервальный, то в качестве значения признака в каждой группе берём середины интервала



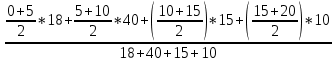
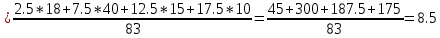лет


Тема Показатели динамики
По данным выпуска товарной продукции рассчитать аналитические показатели динамики и заполнить таблицу

Месяцы
Выпуск товарной продукции,

тыс. руб.
Показатели динамики

Абсолютный прирост (),

тыс. руб.
темп роста,

% (Тр)
темп прироста, % (Тпр)
Абсолютное значение 1% прироста,

тыс. руб. (А)

Цепной
Базисный
цепной
базисный

1

236



















2

244

8
103,38
103,38
3,38
3,38
2.36

3

246

2
101,00
104,23
1,00
4,23
2.44

4

249

3
101,21
105,50
1,21
5,50
2.46

5

250

1
100,40
105,93
0.40
5,93
2.49

6

252

2
101,80
106,77
1,80
6,77
2.5


Решение

Абсолютный прирост:
∆уц=уn-уn-1,
где yn,n-1 – значение показателя в периоде n и (n-1).

Базисный абсолютный прирост (Δyб) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения
∆уб=уn-у0,
где y0 – значение показателя в базисном периоде.

Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.

Цепной темп роста исчисляют отношением текущего уровня к предыдущему:

Трц=уn/уn-1∙100


Базисный темп роста: отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения
Трб=уn/у0∙100

Темп прироста (Тпр) так же может быть цепной или базисный.

Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики

Тпрц=∆уц/уt-1∙100
Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики
Трб=∆уб/у0∙100
Абсолютное значение 1% прироста:
А%ц=уi-1/100%
Тема Индексы
По данным таблицы рассчитать сводные индексы стоимостного объема продукции, физического объема продукции и цен.

Исходные данные


Виды

продукции

Количество произведенной продукции, тыс. шт.
Цена 1 шт., тыс. руб.

базисный период (q0)
Отчетный период (q1)
базисный период (p0)
отчетный период (p1)

А

4402

4452

0,6

0,5

Б

1248

1150
1,2

0,8


Решение:
Сводный индекс товарооборота:

Ipq=q1p1/q0p0,

где    q0,1 – физический объем продаж базисного и отчетного периодов;

р0,1 – цена базисного и отчетного периодов.




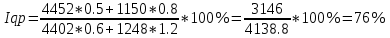
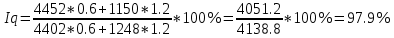
Тема Графическое изображение статистических данных
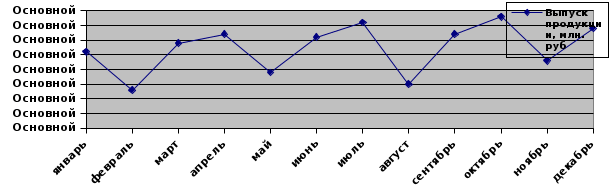
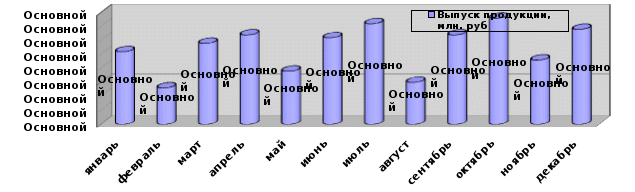
По данным таблицы построить графики динамики в виде линейной и столбиковой диаграмм



Месяцы
Выпуск продукции,

млн. руб.
Месяцы
Выпуск продукции,

Млн.руб.

Январь
18,6
Июль
19,6

Февраль
17,3
Август
17,5

Март
18,9
Сентябрь
19,2

Апрель
19,2
Октябрь
19,8

Май
17,9
Ноябрь
18,3

Июнь
19,1
Декабрь
19,4







Тема Взаимосвязи экономических явлений
По данным таблицы построить аналитическое уравнение зависимости разряда рабочих от стажа работы .С помощью линейного коэффициента корреляции определить тесноту связи между явлениями.


№ n/n рабочих
1
2
3
4
5
6
7
8
9
10
11
12

Разряд (у)
3
2
4
5
5
5
5
5
6
5
1
4

Стаж работы, лет (х)
7
7
25
23
18
24
11
16
34
11
1
20


Решение:

Линейное однофакторное уравнение регрессии имеет вид:



Коэффициенты уравнения регрессии вычисляются по формулам:



Для расчета коэффициентов строится вспомогательная табл.4.
Построим вспомогательную таблицу:


№ п/п
х
у
х2
у2
ху
ух

1
7
3
49
9
21
3,1

2
7
2
49
4
14
3,1

3
25
4
625
16
100
5,2

4
23
5
529
25
115
4,9

5
18
5
324
25
90
4,4

6
24
5
576
25
120
5,1

7
11
5
121
25
55
3,5

8
16
5
256
25
80
4,1

9
34
6
1156
36
204
6,2

10
11
5
121
25
55
3,5

11
1
1
1
1
1
2,4

12
20
4
400
16
80
4,6

Итого
197
50
4207
232
935
50

Среднее
197/12=16,4
4,2
350,6
19,3
77,9
-

Смотрите также файлы