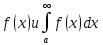
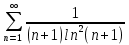
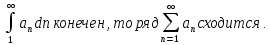
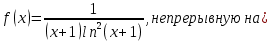
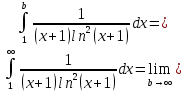
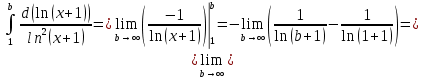
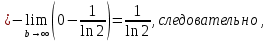
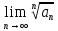
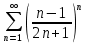
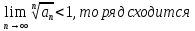
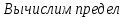
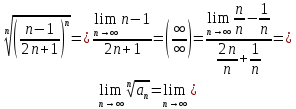
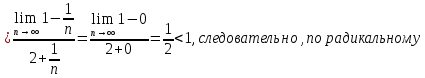
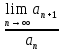
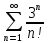
1.1.53. РешениеВоспользуемся интегральным признаком Коши: если интегралРассмотрим функциюВычислим несобственный интегралпо интегральному признаку Коши ряд сходится.Ответ: ряд сходится.1.1.45.РешениеПрименим радикальный признак Коши: если пределпризнаку Коши ряд сходится.Ответ: ряд сходится.1.1.38. Исследовать ряд на сходимость, применяя признак Даламбера. 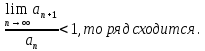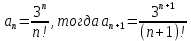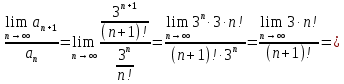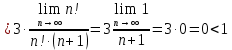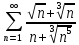Указать РешениеПрименим признак Даламбера: если пределОбщий член ряда равенНайдем пределследовательно, по признаку Даламбера ряд сходится.Ответ: ряд сходится1.1.29.РешениеСравним данный ряд со сходящимся обобщенным гармоническим рядом.

---

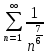
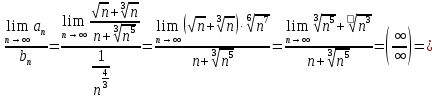
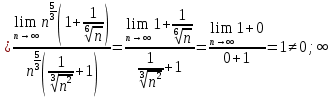
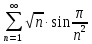
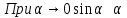
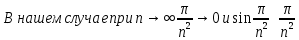
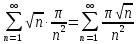
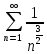
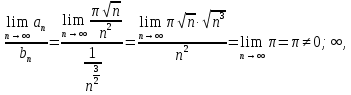
Найдем предел отношенияПредел конечен и не равен нулю, следовательно, по второму признаку сравнения оба ряда сходятся.Ответ: ряд сходится.1.1.32. РешениеВоспользуемся эквивалентностью бесконечно малых величинПолучаем рядСравним полученный ряд со сходящимся обобщенным гармоническим рядом.Найдем предел отношенияследовательно, по второму признаку сравнения оба ряда сходятся.Ответ: ряд сходится.1.1.20. 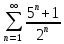РешениеПри отбрасывании в числителе дроби 1, дробь уменьшится. 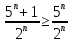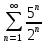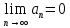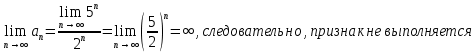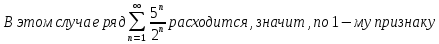ТогдаРассмотрим ряд и проверим выполнение необходимого признака сходимости рядасравнения расходится и исходный ряд.Ответ: ряд расходится.

---

Смотрите также файлы

• У сотрудников есть возможность и карьерного развития. Бизнес компании специфичен, нужны люди, хорошо знающие его.docx

• Учимся разбирать слово по составу.docx

• Отчет и статистическая карточка. Служебное задание не разрабатывается.docx

• Контрольные вопросы. Номинальный фонд времени, применяемый при расчете баланса рабочего времени на предприятии планового фонда.doc

• Задание 21 Рисунок 21. 1 создаем таблицу сотрудников и отделов.docx