се электрические цепи подчиняются первому и второму законам (правилам) Кирхгофа.

Первый закон Кирхгофа можно сформулировать двояко:

1) алгебраическая сумма токов, подтекающих к любому узлу схемы, равна нулю;

2) сумма подтекающих к любому узлу токов равна сумме утекающих от узла токов.

Применительно к рис. 2.8, если подтекающие к узлу токи считать положительными, а утекающие — отрицательными, то согласно первой формулировке

согласно второй —

Физически первый закон Кирхгофа означает, что движение зарядов в цепи происходит так, что ни в одном из узлов они не скапливаются.

Если мысленно рассечь любую схему произвольной плоскостью и все находящиеся по одну сторону от нее рассматривать как некоторый большой «узел», то алгебраическая сумма токов, входящих в этот «узел», будет равна нулю.

Второй закон Кирхгофа также можно сформулировать двояко:

1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:

(в каждую из сумм соответствующие слагаемые входят со знаком плюс, если они совпадают с направлением обхода контура, и со знаком минус, если они не совпадают с ним);

2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю:

Для периферийного контура схемы рис. 2.9

Законы Кирхгофа справедливы для линейных и нелинейных цепей при любом характере изменения во времени токов и напряжений.

Сделаем два замечания: 1) запись уравнения по второму закону Кирхгофа в форме (2.4) может быть получена, если обойти какой-либо контур некоторой схемы и записать выражение для потенциала произвольной точки этого контура через потенциал этой же точки (взяв ее за исходную при обходе) и падения напряжения и ЭДС; 2) при записи уравнений по второму закону Кирхгофа в форме (2.4а) напряжения Uklучастков цепи включают в себя и падения напряжения участков, и имеющиеся на этих участках ЭДС.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает. i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений 

для переменных напряжений 

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

---

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит   узлов, то она описывается   уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит   ветвей, из которых содержат источники тока ветви в количестве , то она описывается   уравнениями напряжений.

Правила Кирхгофа, записанные для   узлов или   контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.

Перед тем, как составить уравнения, нужно произвольно выбрать:

положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;

положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).

Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.

При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).

В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

---

Количество узлов: 3. 
Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0. 
Количество контуров: 2.
Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

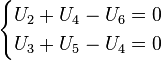
Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей, такой подход к анализу цепи принято называть методом узловых потенциалов.

---

Смотрите также файлы

• Закон Ома для участка цепи с Э.Д.С..docx

• Емкость в цепи синусоидального тока.docx

• ОПУД Тесты (250)..doc

• ИССО. Курсовая работа Водоснабжение и водоотведение..docx

• Реферат Интернет.docx