Файл: Цель работы Экспериментальная проверка теоретического материала, изложенного в лекции. Тонкое кольцо, на котором находится заряд q брусок Шарик, заряд которого равен q х ось кольца, указывающая на положение шарика х ось, указывающая на положение точки под.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 24
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цель работы: Экспериментальная проверка теоретического материала, изложенного в лекции.
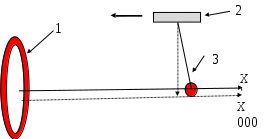

-
Тонкое кольцо, на котором находится заряд Q -
Брусок
-
Шарик, заряд которого равен q.
Х - ось кольца, указывающая на положение шарика
Х - ось, указывающая на положение точки подвеса шарика
Рис.1 Схема установки
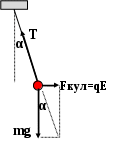
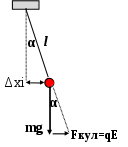
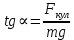
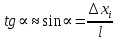
а) б)
Рис.2 Силы, действующие на шарик
Согласно рис 2а, угол отклонения шарика от вертикального положения α связан с силой тяжести шарика и силой, действующий на заряженный шарик со стороны поля, создаваемого кольцом, соотношением: Fкул=mg·tgα.
С другой стороны
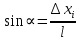 , где
, где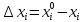 разность между положениями шарика в электрическом поле и при его отcутствии.
разность между положениями шарика в электрическом поле и при его отcутствии.Считая, что угол α мал, можно заменить sinα на tgα и тогда
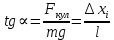
Откуда
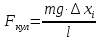
Поделив выражение для кулоновской силы на величину пробного заряда q, получим выражение для напряженности электрического поля, создаваемого заряженным кольцом:
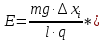 (1)
(1)Согласно теоретическим расчетам, изложенным в лекции, напряженность электрического поля на оси заряженного кольца определяется соотношением:
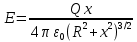 (2)
(2)Исходные данные: R = 10 см = 0,1 м
l = 40 см = 0,4 м
g = 10 м/с²
ɛ₀ = 8,85Е-12 Ф/м
m = 30 гр = 0,03 кг
Q = 3Е-08 Кл
q = 2Е-06 Кл
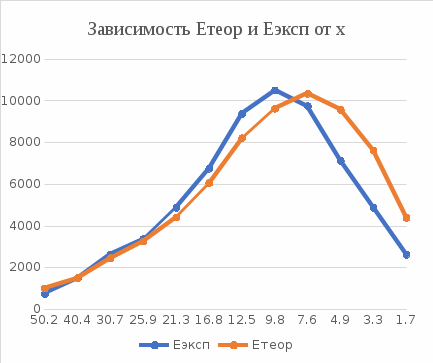
Таблица №2
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| х, см | 50,2 | 40,4 | 30,7 | 25,9 | 21,3 | 16,8 | 12,5 | 9,8 | 7,6 | 4,9 | 3,3 | 1,7 |
| хˈ, см | 50 | 40 | 30 | 25 | 20 | 15 | 10 | 7 | 5 | 3 | 2 | 1 |
| dx, см | 0,2 | 0,4 | 0,7 | 0,9 | 1,3 | 1,8 | 2,5 | 2,8 | 2,6 | 1,9 | 1,3 | 0,7 |
| Еэксп | 750 | 1500 | 2625 | 3375 | 4875 | 6750 | 9375 | 10500 | 9750 | 7125 | 4875 | 2625 |
| Етеор | 1009,263 | 1510,991 | 2459,196 | 3263,183 | 4408,007 | 6061,327 | 8216,311 | 9626,573 | 10341,44 | 9566,954 | 7619,703 | 4391,894 |
| dx, м | 0,002 | 0,004 | 0,007 | 0,009 | 0,013 | 0,018 | 0,025 | 0,028 | 0,026 | 0,019 | 0,013 | 0,007 |
| х, м | 0,502 | 0,404 | 0,307 | 0,259 | 0,213 | 0,168 | 0,125 | 0,098 | 0,076 | 0,049 | 0,033 | 0,017 |
| хˈ, м | 0,5 | 0,4 | 0,3 | 0,25 | 0,2 | 0,15 | 0,1 | 0,07 | 0,05 | 0,03 | 0,02 | 0,01 |
Здесь Еэксп вычисляется по формуле (1), а Етеор по формуле (2).
Чтобы найти положение максимума Етеор, тоесть х, найдем экстремум полученной функции. Для этого возьмем производную от формулы (2) и приравняем к нулю:
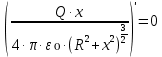
Выносим константы за скобки и сокращаем:
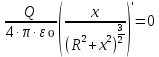
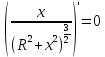
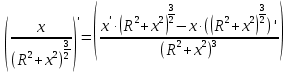 (3)
(3)где:
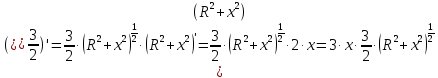
Тогда уравнение (3) принимает вид:
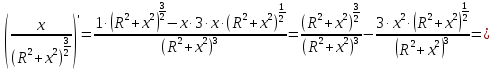
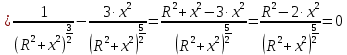
Отсюда следует, что
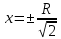
Заданный диапазон от 1,7 см до 50,2 см содержит только положительные числа, отбрасываем отрицательный корень.
Тогда х = 7,1 см (Етеор = макс), а Етеор в этой точке = 10377,9 В/м = Н/Кл