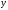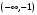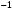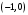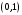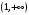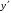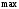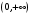Добавлен: 08.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
Институт химии и энергетики
(наименование института полностью)
Кафедра /департамент /центр1 Кафедра Электроснабжения и электротехники
(наименование кафедры/департамента/центра полностью)
ЗАДАНИЕ №
по дисциплине (учебному курсу) «Высшая математика 2»
(наименование дисциплины (учебного курса)
Вариант __5__ (при наличии)
| Студент | Орлов Роман Евгеньевич (И.О. Фамилия) | |
| Группа | ЭЭТбп-2001в | |
| Преподаватель | Крылова Светлана Александровна (И.О. Фамилия) | |
Тольятти 2023
Бланк выполнения задания 2
| № п/п | Задача | Ответ | ||||||||||||||||||||||
| 1. | Рассчитать наибольшее и наименьшее значения функции на заданном отрезке: 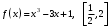 | 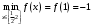 , ,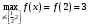 | ||||||||||||||||||||||
| 1) Найти первую производную и все критические точки: | ||||||||||||||||||||||||
| Подробное решение: 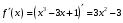 , ,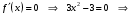 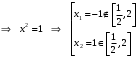 | ||||||||||||||||||||||||
| 2) Вычислить значения функции в критических точках: | ||||||||||||||||||||||||
| Подробное решение: 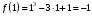 | ||||||||||||||||||||||||
| 3)Вычислить значения функции на концах промежутка: | ||||||||||||||||||||||||
| Подробное решение: 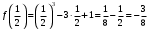 , ,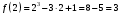 | ||||||||||||||||||||||||
| 4)Сравнить все полученные значения функции и выбрать среди них самое большое и самое малое: | ||||||||||||||||||||||||
| Подробное решение: 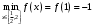 , ,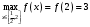 | ||||||||||||||||||||||||
| 2а. | Провести полное исследование и построить графики данных функций: 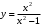 | Построить график, используя полученные результаты | ||||||||||||||||||||||
| Найти область определения функции, исследовать её поведение на границах этой области: | 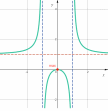 | |||||||||||||||||||||||
| Подробное решение: Область определения равна 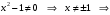 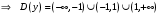 . .Вычислим пределы на бесконечностях: 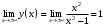 . .Таким образом, при 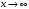 график функции стремится к график функции стремится к 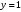 , то есть, прямая , то есть, прямая 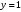 является горизонтальной асимптотой. является горизонтальной асимптотой. | ||||||||||||||||||||||||
| Найти точки разрыва и классифицировать их с помощью односторонних пределов: | ||||||||||||||||||||||||
| Подробное решение: Точки разрыва найдены в предыдущем пункте: 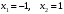 . .Точка 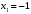 : :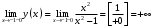 , ,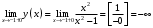 . .Пределы бесконечные, значит, в точке 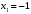 разрыв второго рода. разрыв второго рода.Точка 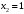 : :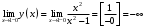 , ,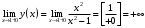 . .Пределы бесконечные, значит, в точке 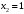 разрыв второго рода. разрыв второго рода. | ||||||||||||||||||||||||
| Исследовать периодичность, чётность (нечётность): | ||||||||||||||||||||||||
| Подробное решение: Функция непериодична. Функция четна: 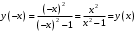 . .Значит, график симметричен относительно оси ординат. | ||||||||||||||||||||||||
| Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции: | ||||||||||||||||||||||||
| Подробное решение: Так как 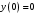 , то график проходит через начало координат. Других точек пересечения с осями нет. , то график проходит через начало координат. Других точек пересечения с осями нет.Промежутки знакопостоянства:
| ||||||||||||||||||||||||
| Найти асимптоты: | ||||||||||||||||||||||||
| Подробное решение: Так как в точках 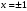 односторонние пределы неограниченны, то прямые односторонние пределы неограниченны, то прямые 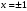 являются вертикальными асимптотами. Находим наклонные асимптоты являются вертикальными асимптотами. Находим наклонные асимптоты 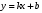 : :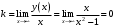 . .Так как 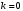 , то наклонных асимптот нет. , то наклонных асимптот нет.При 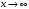 есть горизонтальная асимптота есть горизонтальная асимптота 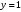 . . | ||||||||||||||||||||||||
| Найти точки экстремума и интервалы монотонности: | ||||||||||||||||||||||||
| Подробное решение: Первая производная равна 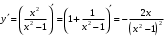 . .Производная определена на 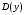 . .Нули производной: 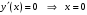 . .Исследуем изменение знака производной при переходе через полученную точку, а также точки 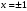 : :
| ||||||||||||||||||||||||
| Найти точки перегиба и интервалы выпуклости и вогнутости: | ||||||||||||||||||||||||
| Подробное решение: Вторая производная равна: 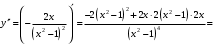 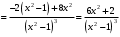 . .Вторая производная определена на 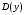 и всюду на ней и всюду на ней 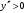 , значит, график всюду вогнут. Точек перегиба нет. , значит, график всюду вогнут. Точек перегиба нет. | ||||||||||||||||||||||||
| 2б. | Провести полное исследование и построить графики данных функций: 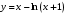 | Построить график, используя полученные результаты | ||||||||||||||||||||||
| Найти область определения функции, исследовать её поведение на границах этой области: | 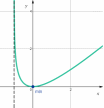 | |||||||||||||||||||||||
| Подробное решение: Логарифм определен лишь для положительных чисел, значит, 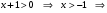 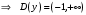 . .Так как 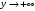 при при 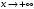 , то на бесконечности график бесконечно возрастает. , то на бесконечности график бесконечно возрастает.Вычислим правосторонний предел в точке 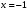 : :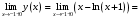 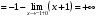 . . | ||||||||||||||||||||||||
| Найти точки разрыва и классифицировать их с помощью односторонних пределов: | ||||||||||||||||||||||||
| Подробное решение: Функция непрерывна на 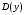 . . | ||||||||||||||||||||||||
| Исследовать периодичность, чётность (нечётность): | ||||||||||||||||||||||||
| Подробное решение: Функция непериодична. Является функцией общего вида (ни четная, ни нечетная) | ||||||||||||||||||||||||
| Найти точки пересечения графика с осями координат и интервалы знакопостоянства функции: | ||||||||||||||||||||||||
| Подробное решение: Так как 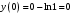 , то график проходит через начало координат. Других точек пересечения с осями нет. , то график проходит через начало координат. Других точек пересечения с осями нет.Промежутки знакопостоянства:
| ||||||||||||||||||||||||
| Найти асимптоты: | ||||||||||||||||||||||||
| Подробное решение: Вертикальная асимптота: 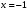 . Найдем наклонные асимптоты . Найдем наклонные асимптоты 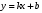 : :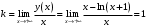 , ,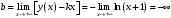 . .Значит, наклонных асимптот нет. | ||||||||||||||||||||||||
| Найти точки экстремума и интервалы монотонности: | ||||||||||||||||||||||||
| Подробное решение: Первая производная: 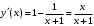 . .Производная определена на 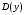 . .Нули производной: 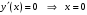 . .Исследуем изменение знака производной при переходе через полученную точку:
| ||||||||||||||||||||||||
| Найти точки перегиба и интервалы выпуклости и вогнутости: | ||||||||||||||||||||||||
| Подробное решение: Вторая производная: 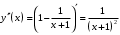 . .Вторая производная определена на 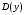 и всюду на ней и всюду на ней 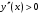 , значит, график всюду вогнут. , значит, график всюду вогнут. |
1 Оставить нужное