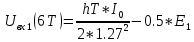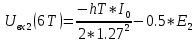Файл: Курсовая работа учебная дисциплина Теория электрической связи.docx
Добавлен: 08.11.2023
Просмотров: 116
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
из методички по курсовой
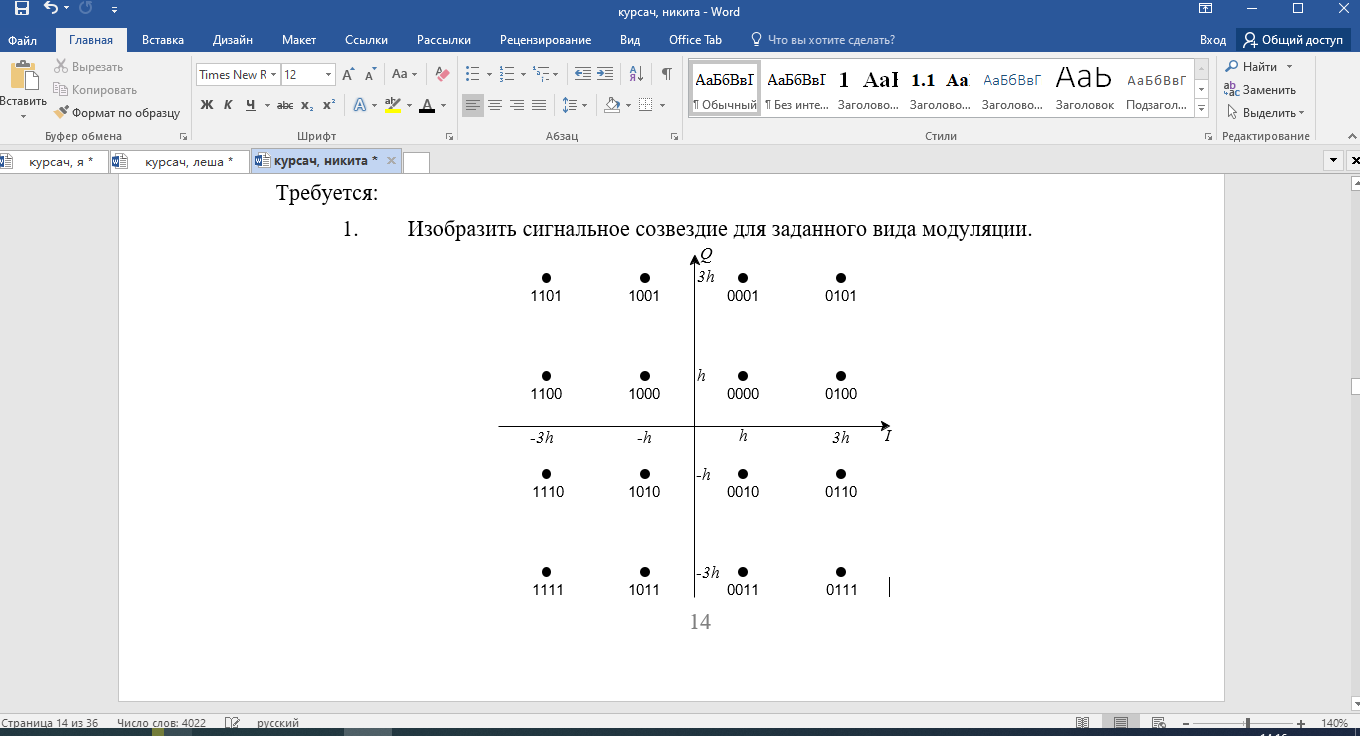
Рис. 10 Сигнальное созвездие для КАМ-16
-
Изобразить график реализации c(t) случайного процесса C(t), формируемого с выхода блока сверточного кодера. Написать аналитическое выражение для случайного процесса С(t)
f
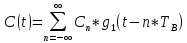
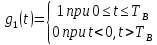
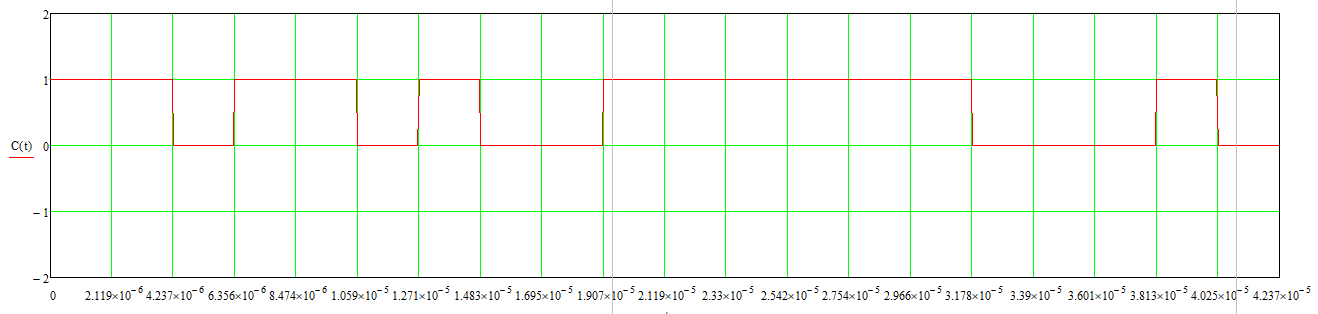
Рис. 11 Реализация случайного процесса
-
В соответствии с сигнальным созвездием модулятора КАМ-16 изобразить графики реализаций i(t) и q(t) на выходе блока ФМС, соответствующие входной реализации с(t). Написать аналитические выражения для случайных процессов I(t) и Q(t).
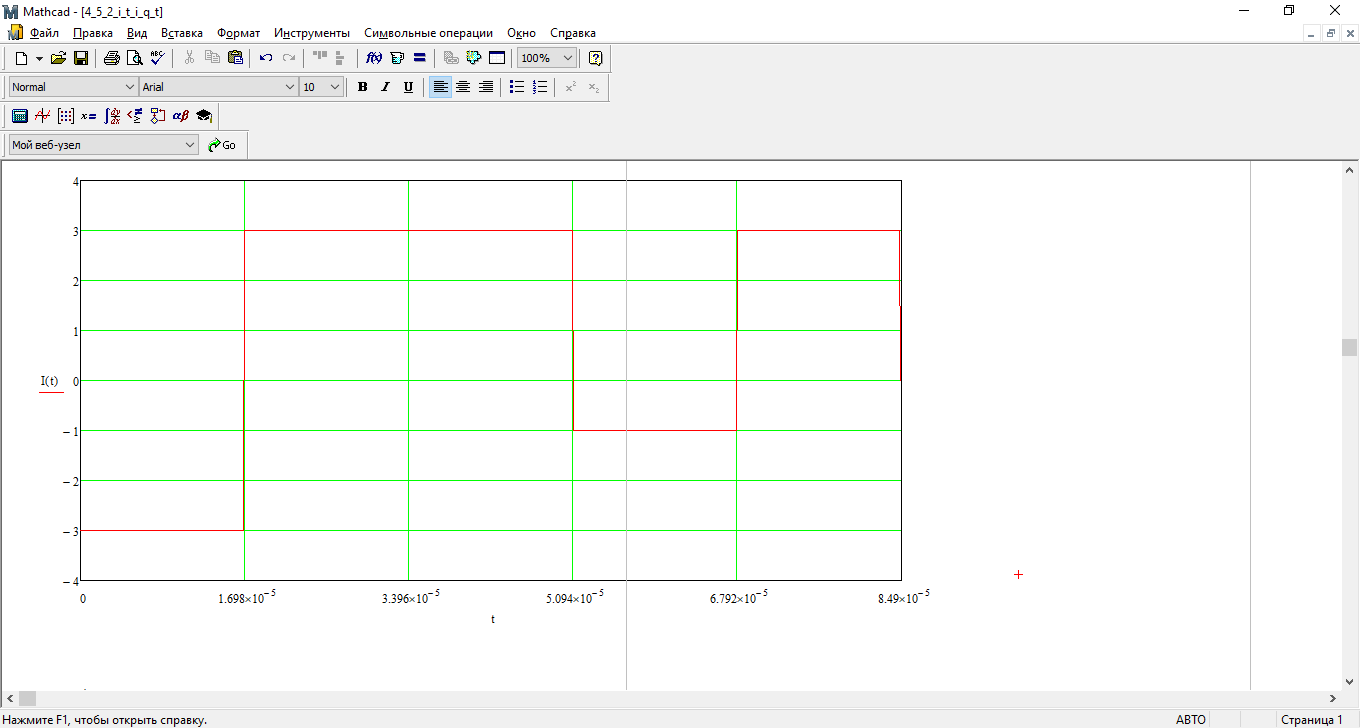
Рис. 12 График i(t)
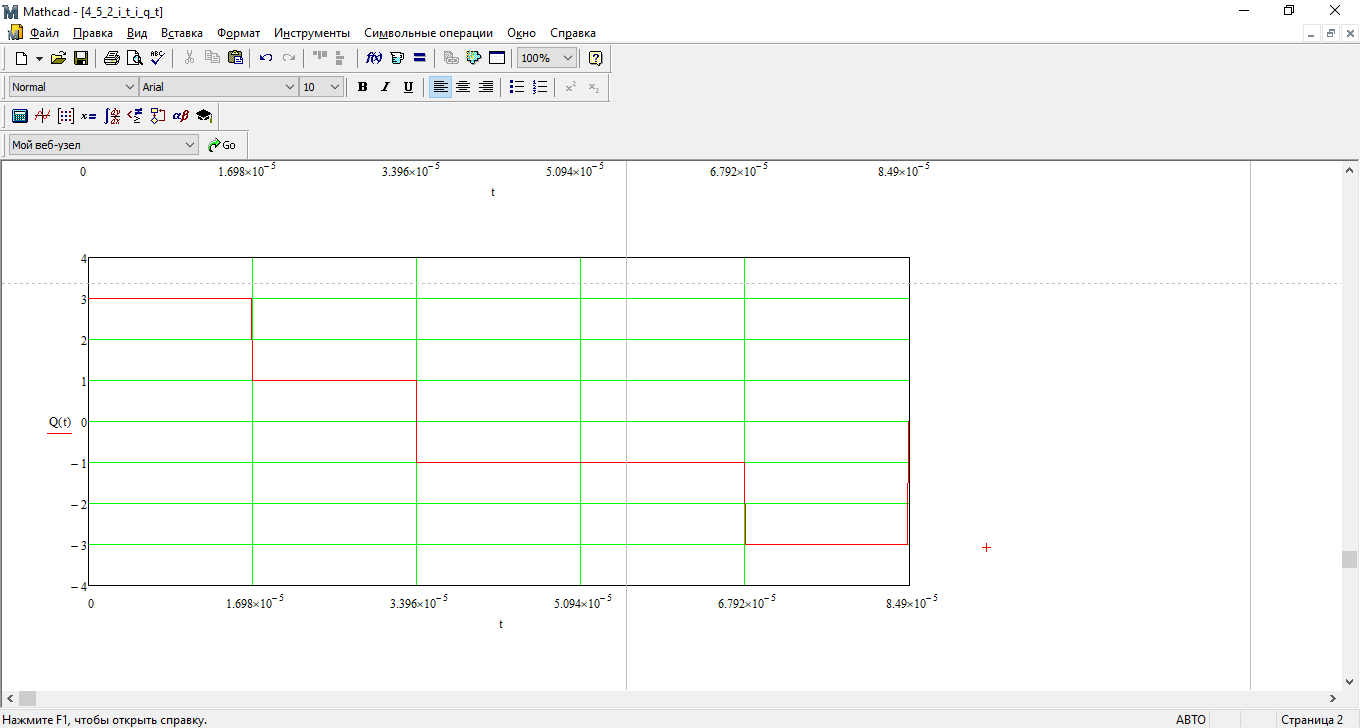
Рис. 13 График q(t)
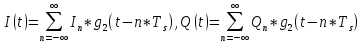
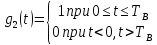
-
Написать аналитические выражения для корреляционной функции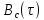 и спектральной плотности
и спектральной плотности 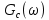 входного случайного процесса C(t) и построить графики этих функций.
входного случайного процесса C(t) и построить графики этих функций.
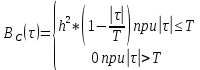
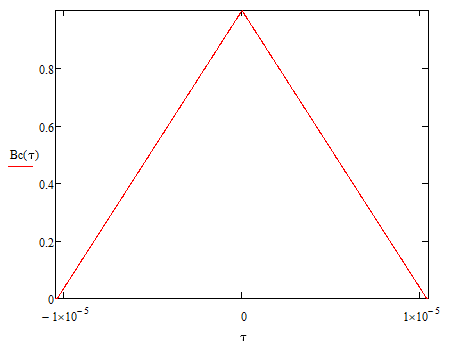
Рис. 14 График корреляционной функции
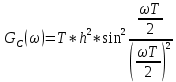


1.22x10^-7
1.5x10^6
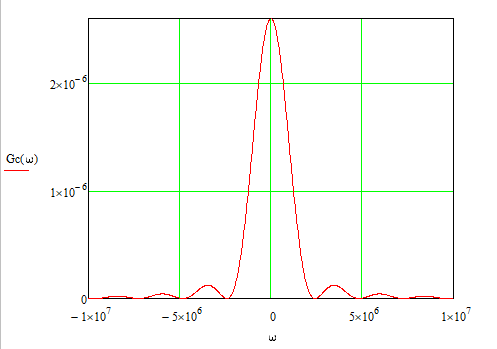
Рис. 15 График спектральной плотности
-
Написать аналитические выражения для корреляционной функции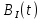 и
и 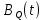 , спектральных плотностей мощности
, спектральных плотностей мощности 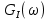 и
и 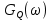 случайных процессов I(t) и Q(t). Построить графики этих функций.
случайных процессов I(t) и Q(t). Построить графики этих функций.

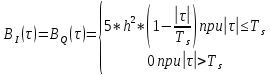
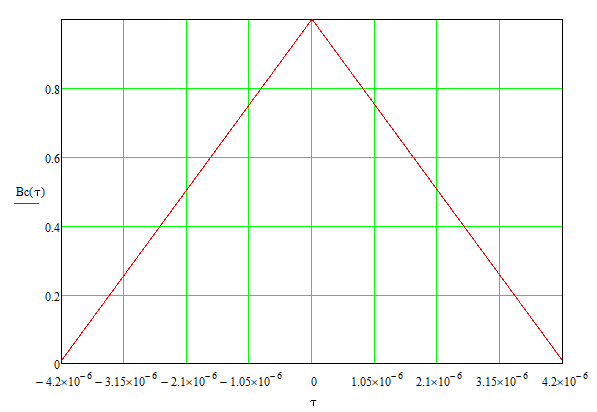
Рис. 16 График корреляционной функции
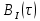
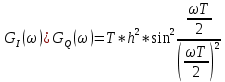
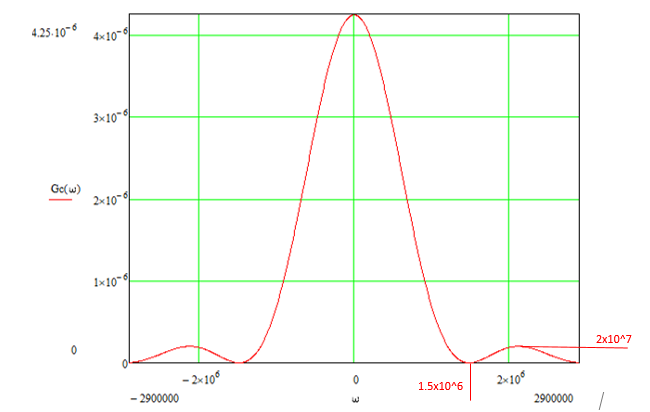
Рис. 17 Спектральная плотность
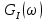
-
Сравнить графики корреляционных функций и спектральных плотностей мощности сигналов на входе и выходе блока ФМС. Привести краткое описание результатов сравнения и, используя общие положения теории преобразования Фурье, пояснить, почему спектр выходных сигналов уже спектра входного сигнала (разд. 4.5).
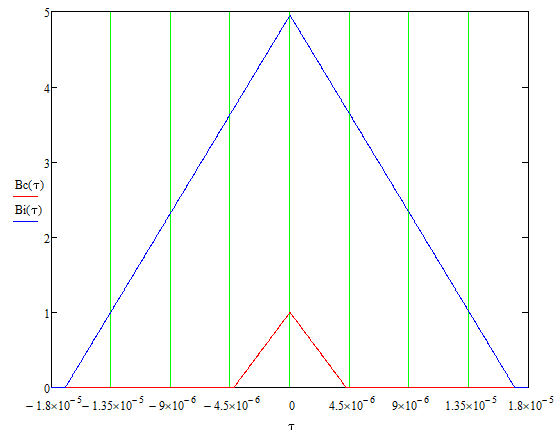
Рис. 18 сравнение графиков корреляционных функций входе и выходе
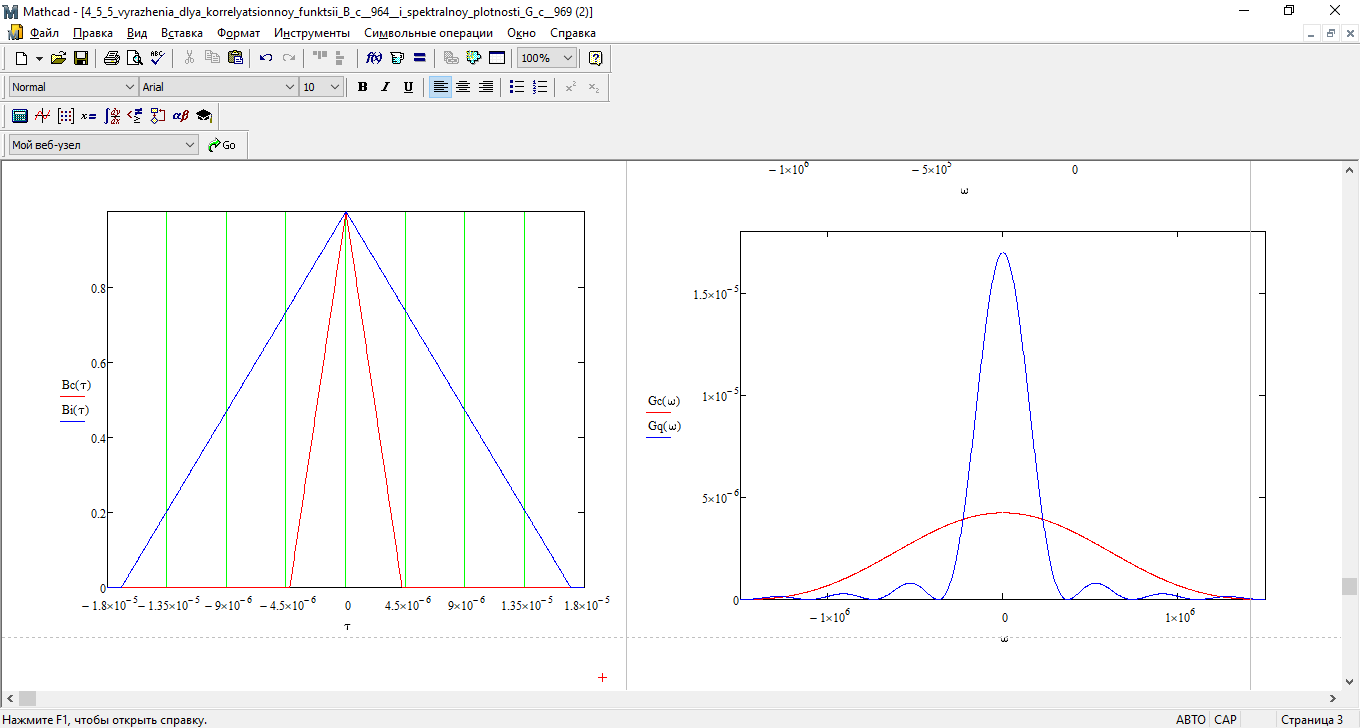
Рис. 19 сравнение графиков спектральных плотностей мощности на входе и выходе
Функции BI(τ) и BQ(τ) отличаются от корреляционной функции BС(τ) тем, что в первом случае используется параметр ТВ, а во втором TS (символьный интервал).
Графики GQ(ω) и GI(ω) будут приблизительно похожи на форму графика GC(ω), но величина главного максимума изменится и будет равна TS∙h2 в точках
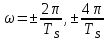
Для КАМ-16 спектр выходных сигналов и длительность параллельных импульсов уже в четыре раза выше, чем последовательного кода при TS = 4∙TB.
-
Модулятор-
Сглаживающий формирующий фильтр.
-
Требуется:
-
Изобразить структурную схему модулятора в составе ЦСС
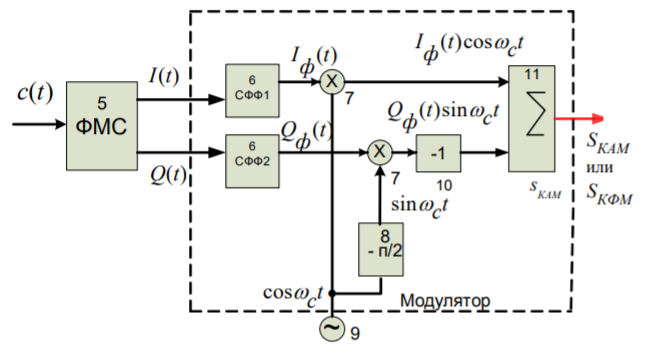
Рис. 20 Расположение блоков СФФ
в схеме цифровой системы связи с квадратурной модуляцией
-
Написать аналитические выражения для сигнала x(t) со «спектром приподнятого косинуса» (импульса Найквиста) и его спектральной плотности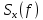 для значений коэффициента сглаживания
для значений коэффициента сглаживания 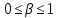 . Изобразить графики сигналов x(t) и соответствующие плотности при
. Изобразить графики сигналов x(t) и соответствующие плотности при 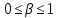 .
.
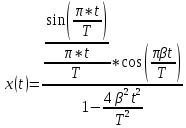
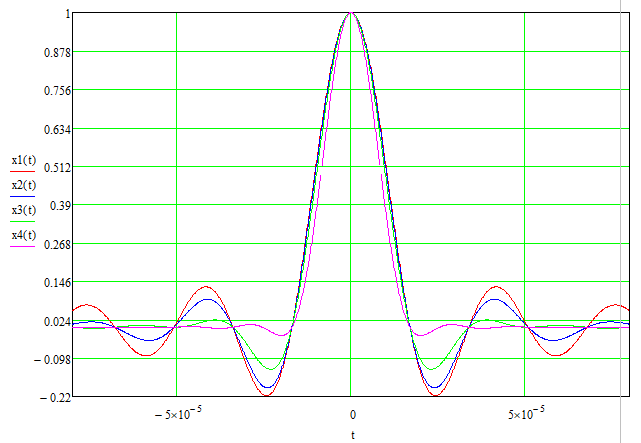
Рис. 21 Графики импульсов Найквиста при
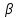 = 0; 0.25; 0.5; 1
= 0; 0.25; 0.5; 1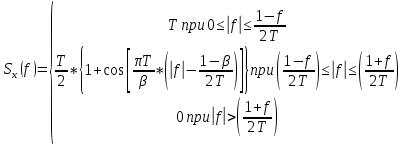
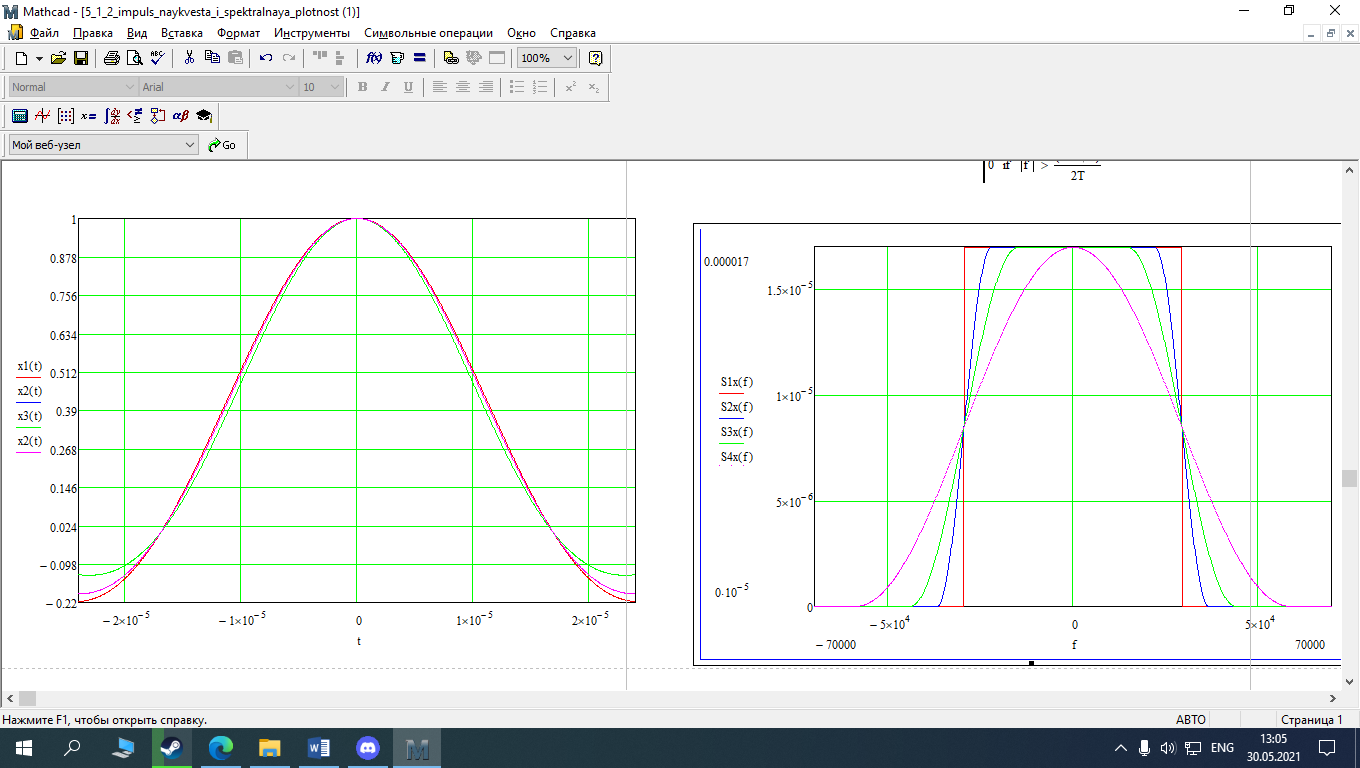
Рис. 22 Графики спектральной плотности импульсов Найквиста при
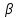 = 0; 0.25; 0.5; 1
= 0; 0.25; 0.5; 1-
На одном рисунке изобразить графики спектральных плотностей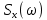 и
и 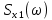 сигналов x(t) и x1(t), где x(t) - импульс Найквиста при коэффициенте сглаживания
сигналов x(t) и x1(t), где x(t) - импульс Найквиста при коэффициенте сглаживания 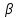 =1, x1(t) - импульс со спектральной плотностью
=1, x1(t) - импульс со спектральной плотностью 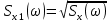
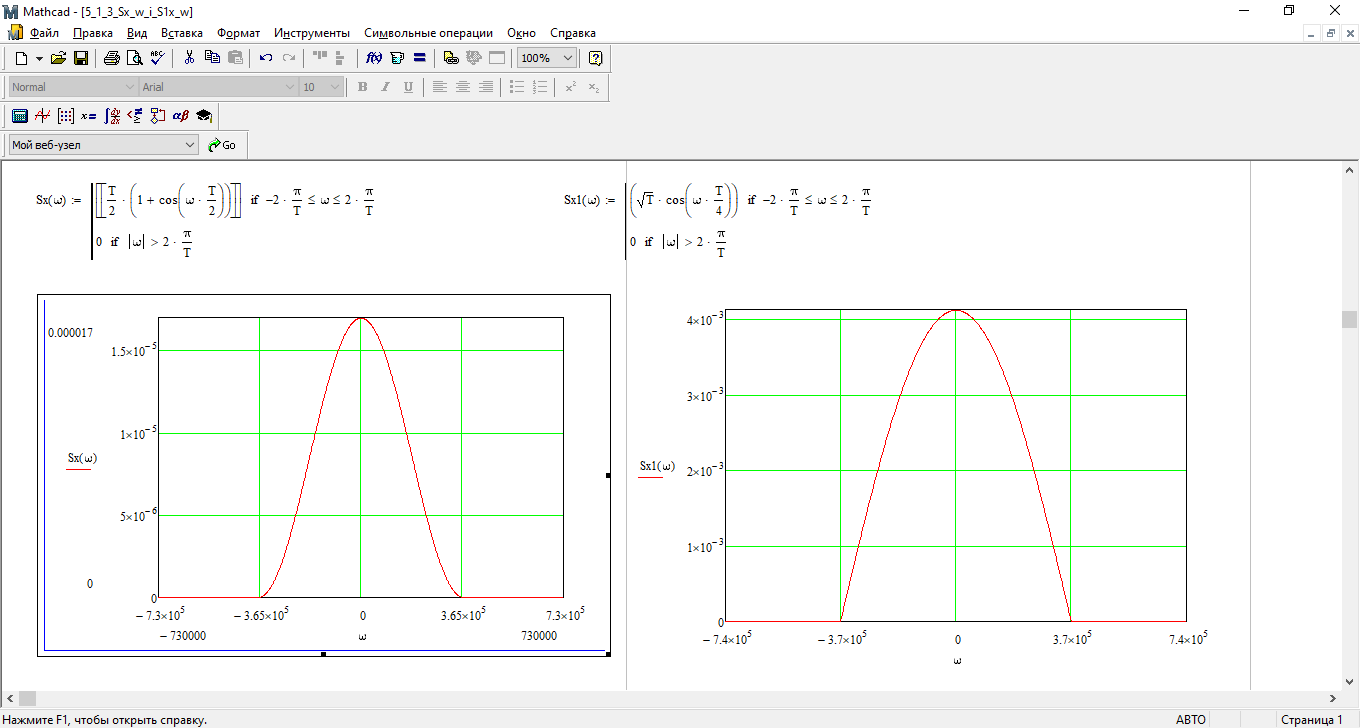
Рис. 23 График спектральной плотности Sx(t)
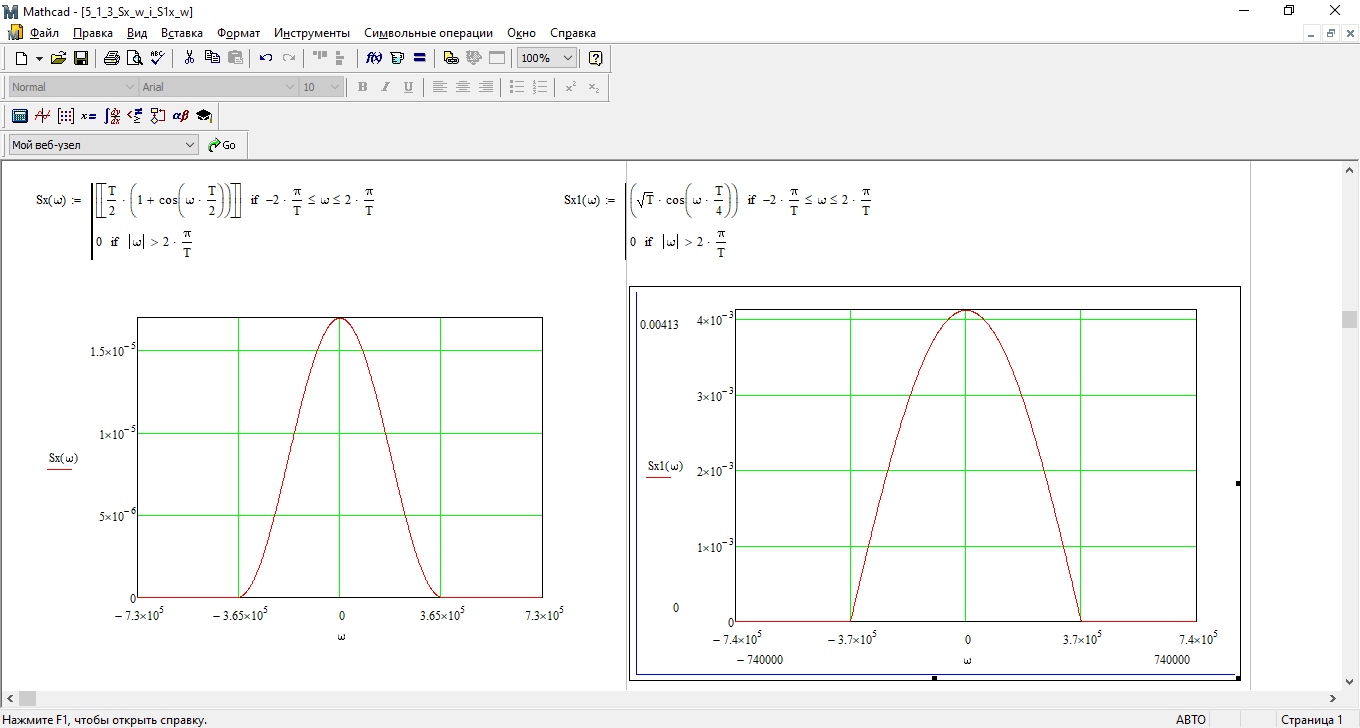
Рис. 24 График спектральной плотности Sx1(t)
-
На одном рисунке изобразить графики импульсов x(t) и x1(t).




-0,073
-0,03
-2x10^-5
-1,6х10^-5
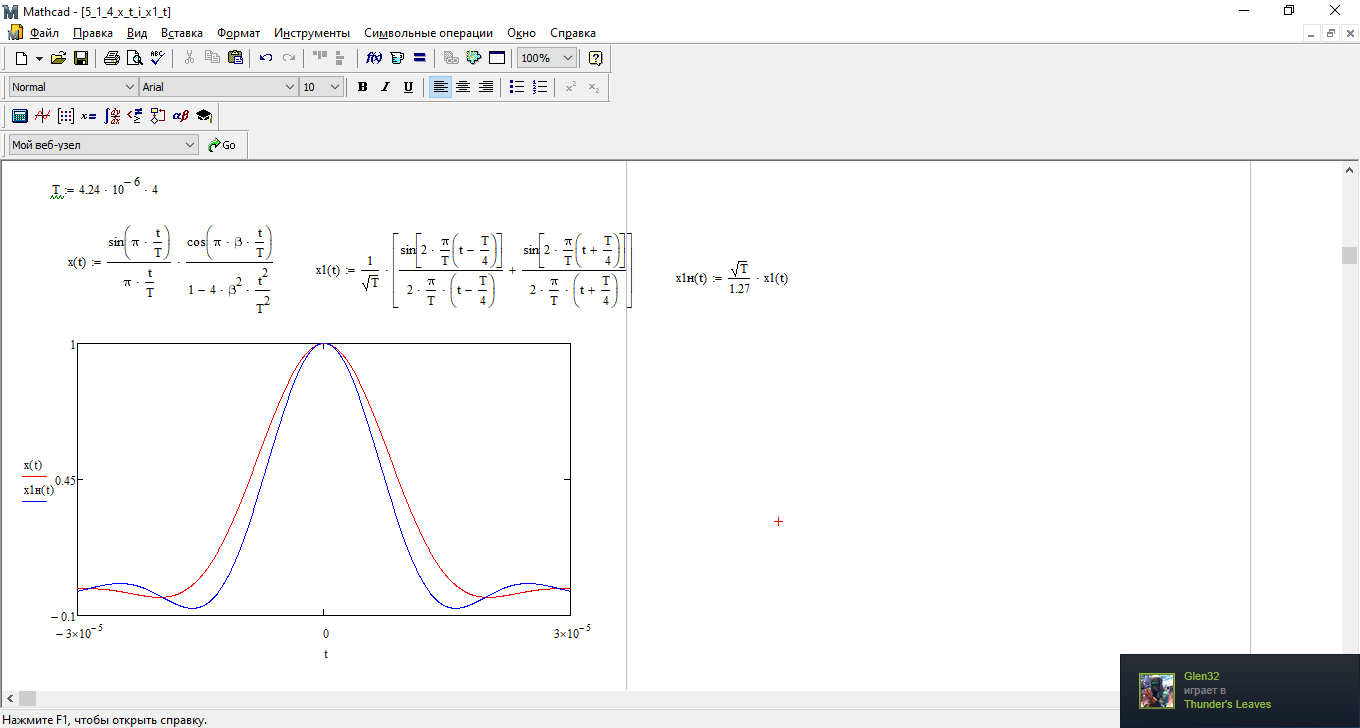
Рис. 25 График импульсов x(t) и x1(t)
-
Написать аналитические выражения для случайных процессов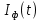 и
и 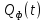
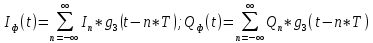
-
Написать аналитические выражения для корреляционных функций и спектральных плотностей мощности случайных процессов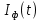 и
и 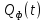 и построить графики этих функций.
и построить графики этих функций.
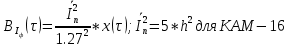
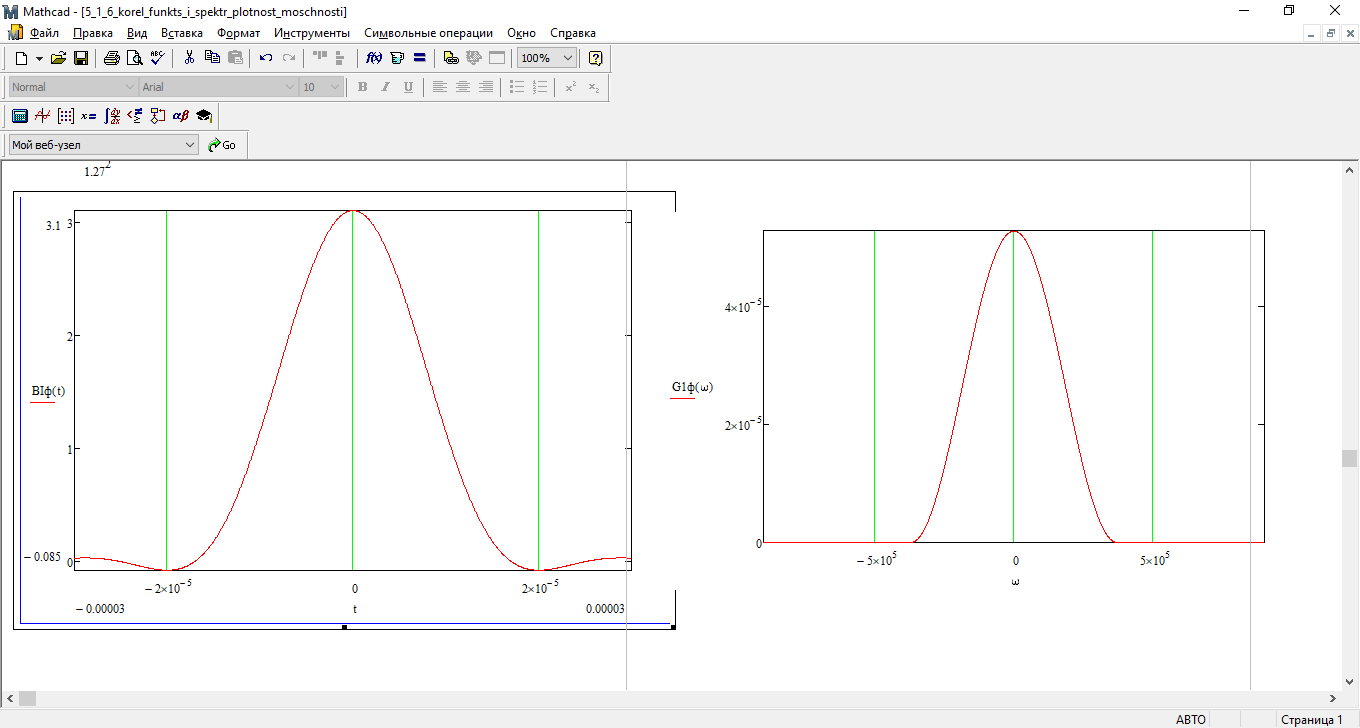

Рис. 26 График корреляционной функции случайных процессов
 и
и 
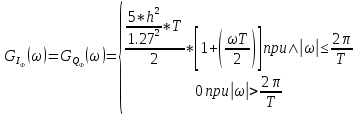
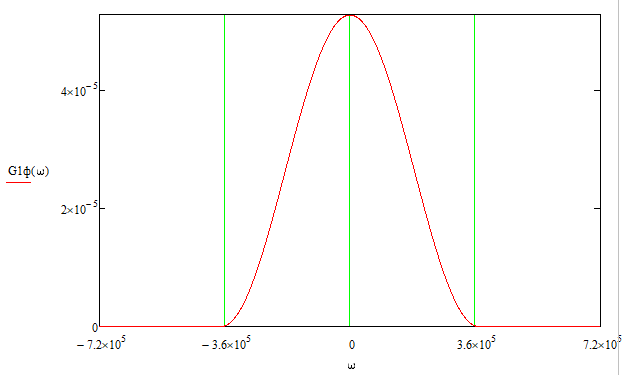
Рис. 27 График спектральной плотности мощности случайных процессов
 и
и 
-
Блоки перемножителей, инвертор, сумматор
Требуется:
-
Написать аналитические выражения для корреляционных функций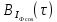 и
и 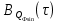 случайных сигналов
случайных сигналов 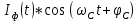 и
и 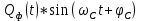 на выходах перемножителей, где
на выходах перемножителей, где 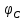 – случайная фаза с равномерной плотностью вероятности на интервале 0…2π. Случайная фаза
– случайная фаза с равномерной плотностью вероятности на интервале 0…2π. Случайная фаза 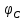 не зависит от случайных процессов
не зависит от случайных процессов 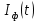 и
и 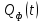 .
.
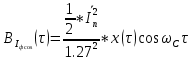
-
Написать аналитические выражения для корреляционной функции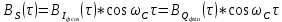 и для спектральной плотности мощности
и для спектральной плотности мощности 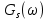 сигнала S(t) на выходе сумматора для заданного вида модуляции. Построить графики этих функций.
сигнала S(t) на выходе сумматора для заданного вида модуляции. Построить графики этих функций.
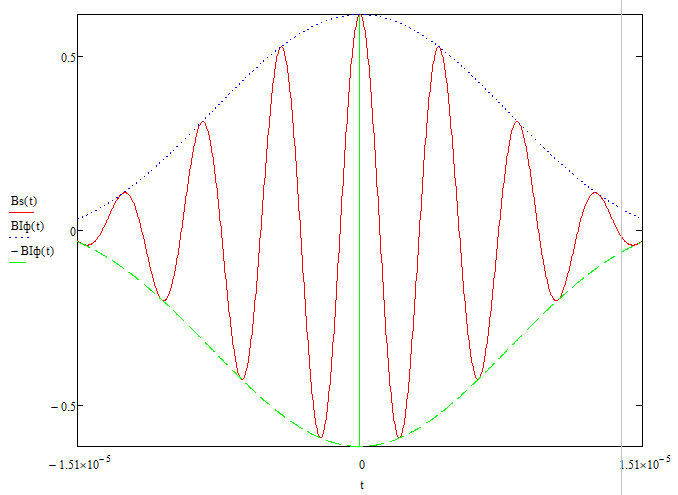
Рис. 28 График корреляционной функции
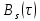
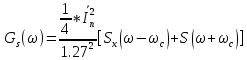
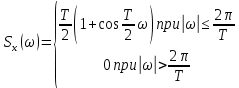
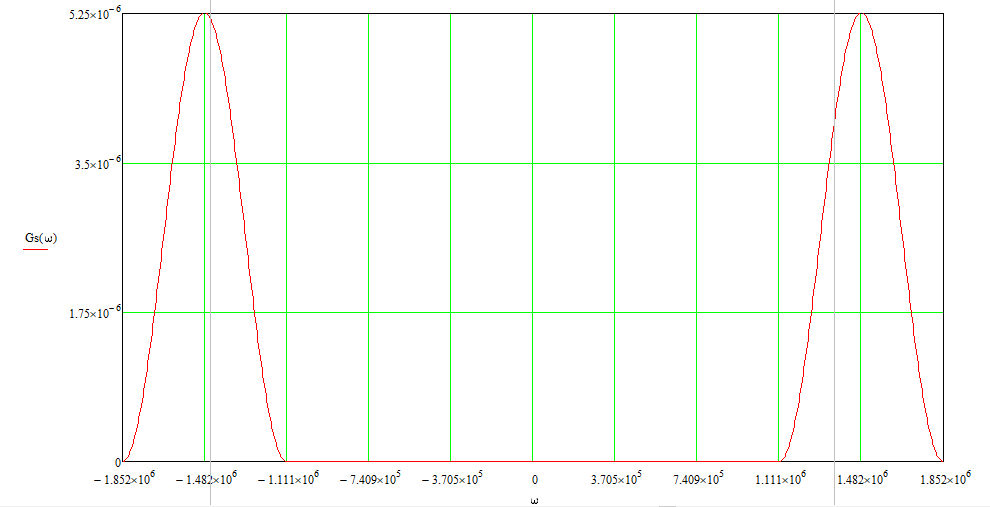
Рис. 29. График спектральной плотности мощности
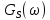
-
Непрерывный канал
Требуется:
-
Определить минимальную ширину полосы частот Fk непрерывного канала, необходимую для передачи по каналу сигнала S(t) с выхода модулятора.
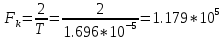
-
Определить PC – среднюю мощность информационного сигнала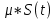 на выходе канала
на выходе канала
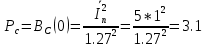
-
Определить Pп – среднюю мощность помехи n(t) на выходе канала и найти отношение Pc/Pп
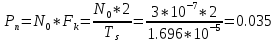
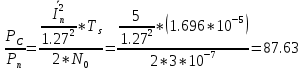
-
Рассчитать пропускную способность С (за секунду) непрерывного канала.
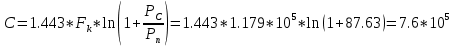
-
Демодулятор
Требуется:
-
Изобразить структурную схему когерентного демодулятора, оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции.
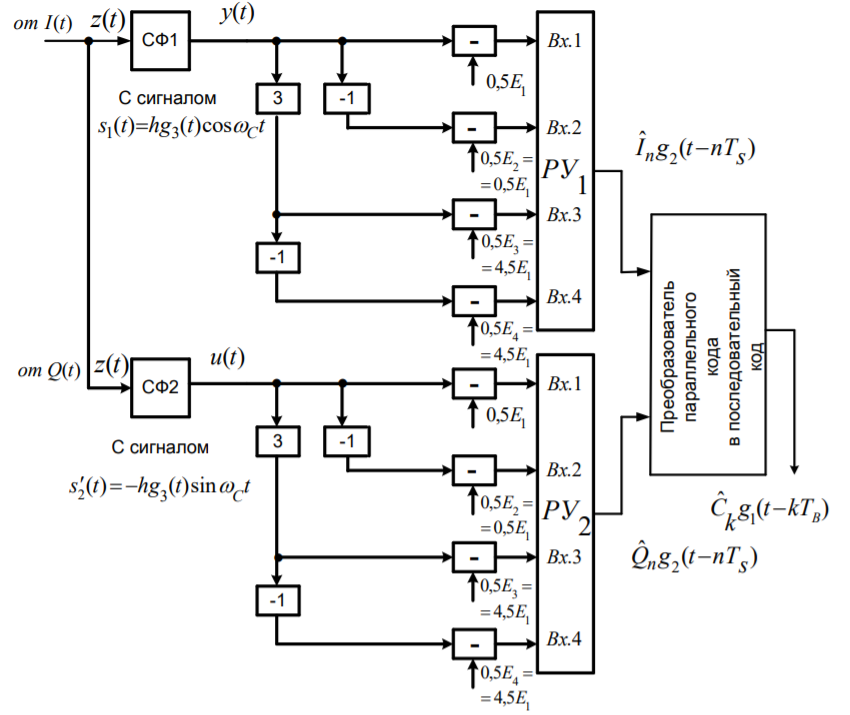
Рис. 30 Структурная схема когерентного демодулятора для сигнала КАМ-16
-
Написать алгоритмы работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора
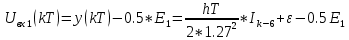
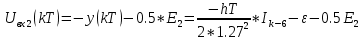
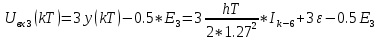
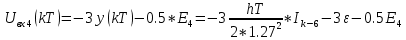
Если в составе сигнала z(t) сигнал помехи n(t) будет равен нулю, то величина ξ также будет равна нулю и напряжения на входах РУ1 согласно будут следующими: