Файл: Федеральное государственное бюджетное образовательное учреждение высшего образования российский университет транспорта.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 241
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, используемых при восстановлении сигнала по его отсчетам.
Дискретизация бывает равномерная и неравномерная. При равномерной дискретизации период отсчетов Т остается постоянным, а при неравномерной может изменяться. Неравномерная дискретизация чаще всего обусловлена скоростью изменения сигнала и поэтому называется адаптивной. В основе равномерной дискретизации лежит теорема отсчётов, согласно которой в качестве коэффициентов an нужно использовать мгновенные значения сигнала U(tn) в дискретные моменты времени tn = Tn, а период дискретизации выбирают из условия Т = (2fm)-1 – теорема Котельникова.
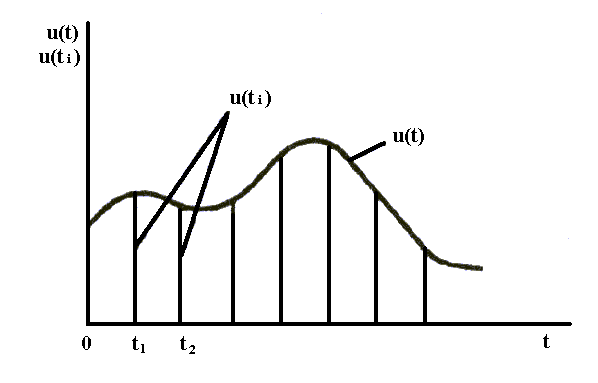
Рис. 1. Процесс дискретизации непрерывного сигнала
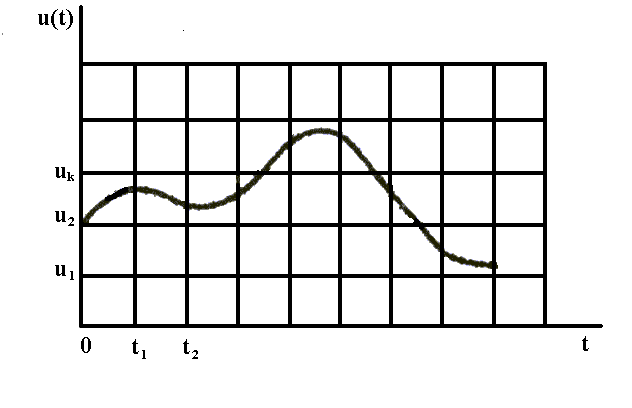
Рис. 2. График квантования сигнала
В отличие от дискретизации, которая теоретически является обратимой операцией, квантование представляет собой необратимое преобразование исходной последовательности и сопровождается появлением неизбежных погрешностей. Характеристика идеального квантования приведена на рис. 3. Разность между двумя соседними значениями квантованной величины называется шагом квантования К.
По существу, квантование представляет собой операцию округления непрерывной величины до ближайшего целого значения. В результате максимальная погрешность квантования равна ± 0,5 К (см. рис. 2). Однако при преобразовании произвольного сигнала максимальная погрешность встречается сравнительно редко, поэтому в большинстве случаев для оценки качества АЦП используют не максимальную, а среднеквадратическую погрешность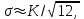
которая примерно в 3,5 раза меньше максимальной. В АЦП погрешность квантования определяется как единица младшего значения разряда.
Выходной величиной АЦП является цифровой код, т.е. последовательность цифр, с помощью которой представляются дискретные квантовые величины. В АЦП используют четыре основных типа кодов: натуральный двоичный, десятичный, двоично-десятичный и код Грея. Кроме этого, АЦП предназначены дня управления семисегментными индикаторами.
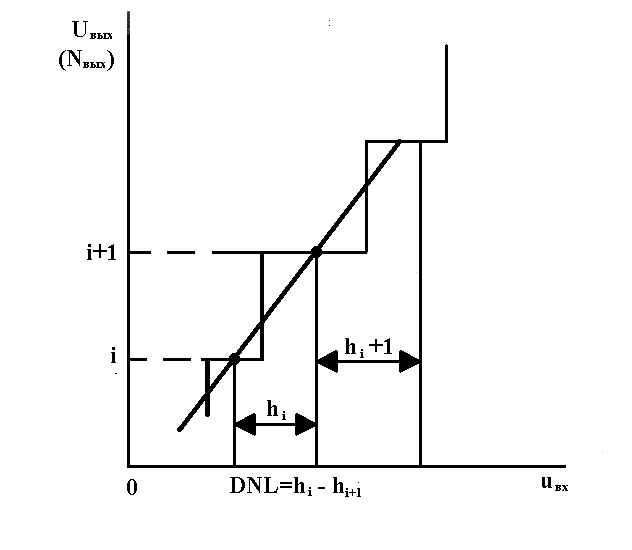
Рис. 3. Определение дифференциальной нелинейности
Большинство АЦП работают с выходом в натуральном двоичном коде, при котором каждому положительному числу N ставится в соответствие код: {bi} = b1 b2…bn, где bi равно нулю или единице. При этом положительное число в двоичном коде имеет вид
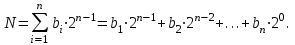
Такой код называется прямым. Прямой код пригоден лишь для работы с однополярными сигналами. Полный диапазон преобразуемого сигнала равен 2n, а Nmax. = 2n-1. При использовании в АЦП двоично-десятичных кодов каждая значащая десятичная цифра представляется четырьмя двоичными знаками и содержит десять значений сигнала от 0 до 9. Так как при кодировании четырьмя двоичными значениями можно получить 16 кодовых значений, то приведенное двоично-десятичное представление не является единственным. Наиболее широко используют коды, в которых цифрам в тетрадях присваивают веса 8 – 4 – 2 – 1 или 2 – 4 – 2 – 1:
АЦП оцениваются по их основным метрологическим характеристикам, которые можно разделить на две группы: статические и динамические.
К статическим характеристикам АЦП относят: абсолютные значения и полярности входных сигналов, входное сопротивление, значения и полярности выходных сигналов, выходное сопротивление, значения напряжений и токов источников питания, количество двоичных кии десятичных разрядов выходного кода, погрешности преобразования постоянного напряжения и др. К динамическим характеристикам АЦП относят: время преобразования, максимальную частоту дискретизации, апертурное время, динамическую погрешность и т.д.
Рассмотрим эти параметры более подробно. Основной характеристикой является разрешающая способность АЦП, которую принято определять величиной, обратной максимальному числу кодовых комбинаций на выходе АЦП. Разрешающую способность можно выражать в процентах, в количестве разрядов или в относительных единицах. Например, 10-разрядный АЦП имеет разрешающую способность (1024)-1 10-3=0,1%. Если напряжение шкалы для такого АЦП равно 10 В, то абсолютное значение разрешающей способности будет около 10 мВ.
Точность АЦП определяется значениями абсолютной погрешности, дифференциальной и интегральной нелинейности. Абсолютную погрешность АЦП определяют в конечной точке характеристики преобразования, поэтому ее называют погрешностью полной шкалы, а измеряют в единицах младшего разряда.
Дифференциальную нелинейность (PNL) определяют через идентичность двух соседних приращений сигнала, т.е. как разность напряжений двух соседних квантов PNL = hi – hi+1. Определение PNL показано на рис. 3.
Интегральная нелинейность АЦП (JNL) характеризует идентичность приращений во всем диапазоне входного сигнала (рис. 6). Она определяется по максимальному отклонению сглаженной характеристики преобразования от идеально прямой линии, т.е. JNL = Ui - Ui, (рис. 4).
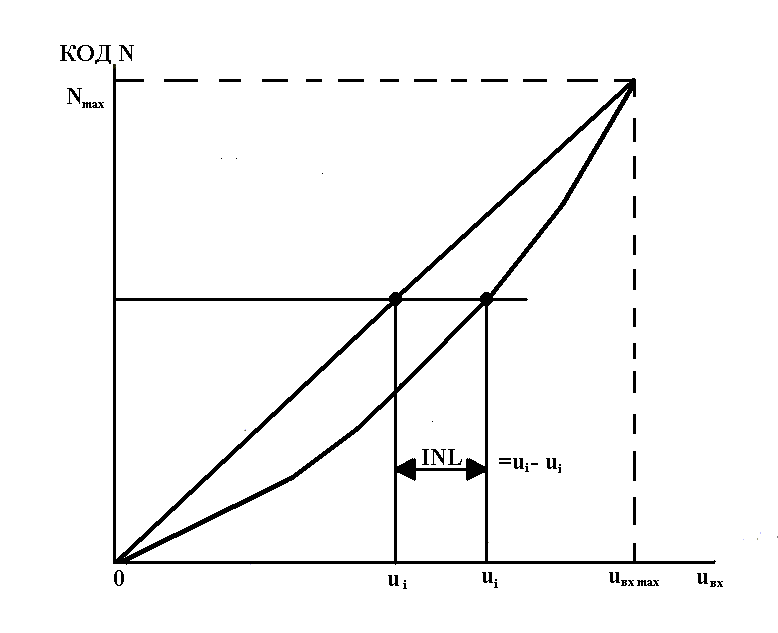
Рис. 4. Определение интегральной нелинейности
Время преобразования Т
пр обычно определяется как интервал времени от начала преобразования до появления на выходе АЦП устойчивого кода. Для одних АЦП это время постоянное и не зависит от входного сигнала, для других зависит. Если АЦП работает без устройства выборки и хранения, то время преобразования является апертурным временем.
Максимальная частота дискретизации - частота, с которой возможно преобразование входного сигнала, при условии, что выбранный параметр не выходит за заданные пределы. Иногда максимальную частоту преобразования принимают равной обратной величине времени преобразования.
АЩП мгновенных значений подразделяют на следующие основные виды: последовательного счета, последовательного приближения, параллельные, параллельно-последовательные и с промежуточным преобразованием в интервале времени. Структурная схема АЦП последовательного счета (рис. 5) содержит компаратор, при помощи которого выполняется сравнение входного напряжения с напряжением обратной связи. На прямой вход компаратора поступает входной сигнал Uвх, а на инвертирующий - напряжение обратной связи. Работа преобразователя начинается с приходом импульса «ПУСК» от схемы управления, который замыкает ключ S. Через замкнутый ключ S импульсы U1 от генератора тактовых импульсов поступают на счетчик, который управляет работой цифро-аналогового преобразователи (ЦАП). В результате последовательного увеличения выходного кода счетчика N происходит последовательно-ступенчатое увеличение выходного напряжения U5 ЦАП. Когда выходное напряжение ЦАП сравняется с входным напряжением, произойдет переключение компаратора, и по его выходному сигналу «СТОП» разомкнется ключ S. В, результате импульсы от генератора перестанут поступать на вход счетчика. Выходной код, соответствующий равенству Uвх=Us, снимается с выходного регистра счетчика.
Графики, иллюстрирующие процесс преобразования напряжения в цифровой код, приведены на рис. б. Из этих графиков следует, что время преобразования зависит отуровни входного напряжения. При числе двоичных разрядов счетчика, равном n, и периоде следования счётных импульсов Т максимальное время преобразования можно определить по формуле
где 0 Кn – число ступеней до момента сравнения;
U – шаг квантования.
Структурная схема АЦП последовательного приближения (рис. 7) отличается от структурной схемы последовательного счета тем, что вместо счетчика импульсов включен регистр последовательных приближений РПП.
В основе РПП лежит принцип дихотомии, т.е. последовательного сравнения преобразуемого напряжения Uвх с ½, ¼, 1/8 и т.д. возможного максимального его значения Um. Это позволяет для n - разрядного АЦП выполнить весь процесс преобразования за п последовательных шагов (итераций) вместо (2n-1) при использовании последовательного счета и получить существенный выигрыш по быстродействию.
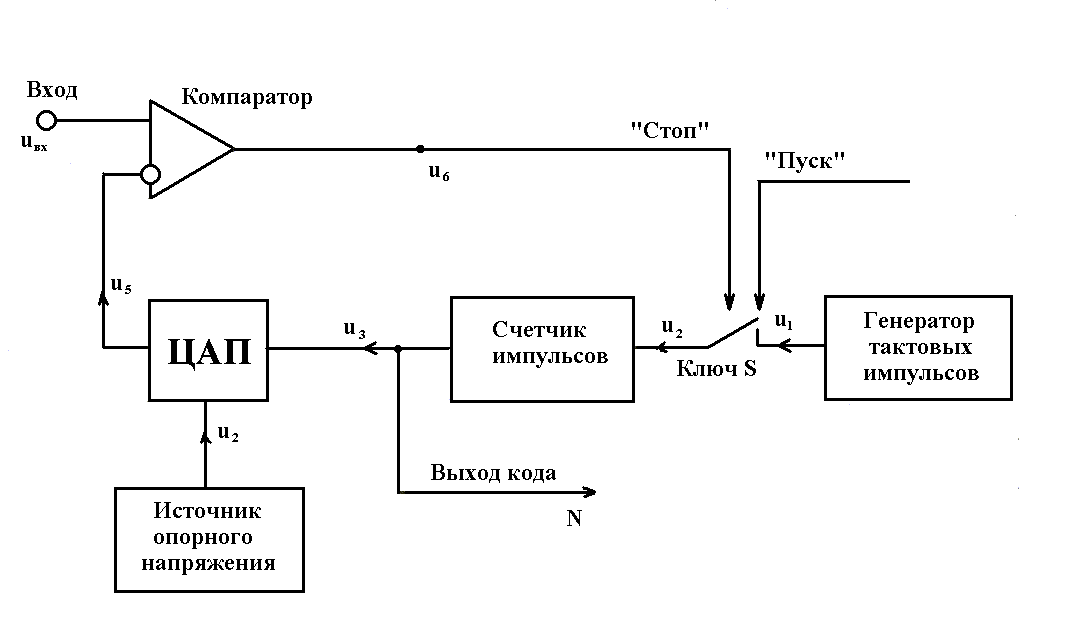
Рис. 5. Структурная схема АЦП последовательного счета
На рис. 7 приведена структурная схема, реализующая метод последовательных приближений. На каждом шаге производится определение одного разряда, начиная со старшего. При первом сравнении определяется, больше или меньше напряжение Uвх, чем Um/2. На следующем шаге определяется, в какой четверти диапазона находится Uвх. Каждый последующий шаг сужает область возможного результата. При каждом сравнении компаратор формирует импульсы, соответствующие состоянию «больше - меньше» (1 или 0), управляющие регистром последовательных приближений.
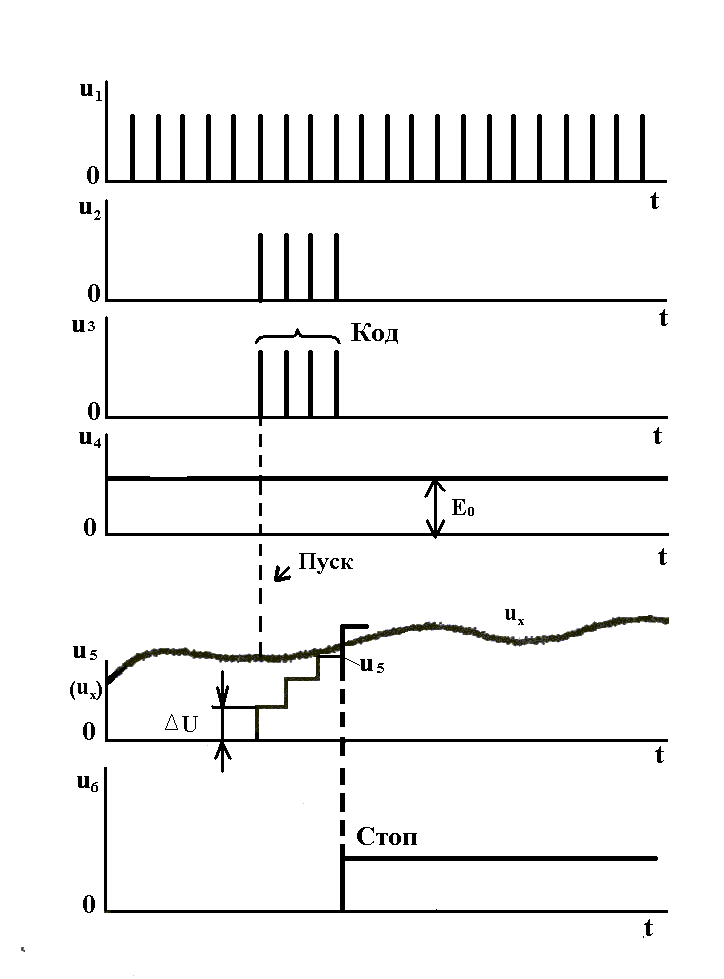
Рис. 6. Временные диаграммы процесса последовательного счета
График процесса последовательного приближения приведен на рис. 8.
Структурная схема параллельного АЦП приведена на рис. 9. Преобразователь осуществляет одновременное квантование входного сигнала Uвх с помощью компараторов, включенных параллельно входному сигналу. Пороговые уровни компараторов установлены с помощью резистивного деления в соответствии с используемой шкалой квантования. На выходах компараторов получаем квантованный сигнал, представленный в унитарном коде.
Дискретизация бывает равномерная и неравномерная. При равномерной дискретизации период отсчетов Т остается постоянным, а при неравномерной может изменяться. Неравномерная дискретизация чаще всего обусловлена скоростью изменения сигнала и поэтому называется адаптивной. В основе равномерной дискретизации лежит теорема отсчётов, согласно которой в качестве коэффициентов an нужно использовать мгновенные значения сигнала U(tn) в дискретные моменты времени tn = Tn, а период дискретизации выбирают из условия Т = (2fm)-1 – теорема Котельникова.
Рис. 1. Процесс дискретизации непрерывного сигнала
Рис. 2. График квантования сигнала
В отличие от дискретизации, которая теоретически является обратимой операцией, квантование представляет собой необратимое преобразование исходной последовательности и сопровождается появлением неизбежных погрешностей. Характеристика идеального квантования приведена на рис. 3. Разность между двумя соседними значениями квантованной величины называется шагом квантования К.
По существу, квантование представляет собой операцию округления непрерывной величины до ближайшего целого значения. В результате максимальная погрешность квантования равна ± 0,5 К (см. рис. 2). Однако при преобразовании произвольного сигнала максимальная погрешность встречается сравнительно редко, поэтому в большинстве случаев для оценки качества АЦП используют не максимальную, а среднеквадратическую погрешность
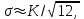которая примерно в 3,5 раза меньше максимальной. В АЦП погрешность квантования определяется как единица младшего значения разряда.Выходной величиной АЦП является цифровой код, т.е. последовательность цифр, с помощью которой представляются дискретные квантовые величины. В АЦП используют четыре основных типа кодов: натуральный двоичный, десятичный, двоично-десятичный и код Грея. Кроме этого, АЦП предназначены дня управления семисегментными индикаторами.
Рис. 3. Определение дифференциальной нелинейности
Большинство АЦП работают с выходом в натуральном двоичном коде, при котором каждому положительному числу N ставится в соответствие код: {bi} = b1 b2…bn, где bi равно нулю или единице. При этом положительное число в двоичном коде имеет вид
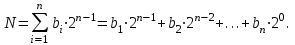
Такой код называется прямым. Прямой код пригоден лишь для работы с однополярными сигналами. Полный диапазон преобразуемого сигнала равен 2n, а Nmax. = 2n-1. При использовании в АЦП двоично-десятичных кодов каждая значащая десятичная цифра представляется четырьмя двоичными знаками и содержит десять значений сигнала от 0 до 9. Так как при кодировании четырьмя двоичными значениями можно получить 16 кодовых значений, то приведенное двоично-десятичное представление не является единственным. Наиболее широко используют коды, в которых цифрам в тетрадях присваивают веса 8 – 4 – 2 – 1 или 2 – 4 – 2 – 1:
| b4 | b3 | b2 | b1 | или | b4 | b3 | b2 | b1 |
| 8 | 4 | 2 | 1 | 2 | 4 | 2 | 1 |
Основные характеристики АЦП
АЦП оцениваются по их основным метрологическим характеристикам, которые можно разделить на две группы: статические и динамические.
К статическим характеристикам АЦП относят: абсолютные значения и полярности входных сигналов, входное сопротивление, значения и полярности выходных сигналов, выходное сопротивление, значения напряжений и токов источников питания, количество двоичных кии десятичных разрядов выходного кода, погрешности преобразования постоянного напряжения и др. К динамическим характеристикам АЦП относят: время преобразования, максимальную частоту дискретизации, апертурное время, динамическую погрешность и т.д.
Рассмотрим эти параметры более подробно. Основной характеристикой является разрешающая способность АЦП, которую принято определять величиной, обратной максимальному числу кодовых комбинаций на выходе АЦП. Разрешающую способность можно выражать в процентах, в количестве разрядов или в относительных единицах. Например, 10-разрядный АЦП имеет разрешающую способность (1024)-1 10-3=0,1%. Если напряжение шкалы для такого АЦП равно 10 В, то абсолютное значение разрешающей способности будет около 10 мВ.
Точность АЦП определяется значениями абсолютной погрешности, дифференциальной и интегральной нелинейности. Абсолютную погрешность АЦП определяют в конечной точке характеристики преобразования, поэтому ее называют погрешностью полной шкалы, а измеряют в единицах младшего разряда.
Дифференциальную нелинейность (PNL) определяют через идентичность двух соседних приращений сигнала, т.е. как разность напряжений двух соседних квантов PNL = hi – hi+1. Определение PNL показано на рис. 3.
Интегральная нелинейность АЦП (JNL) характеризует идентичность приращений во всем диапазоне входного сигнала (рис. 6). Она определяется по максимальному отклонению сглаженной характеристики преобразования от идеально прямой линии, т.е. JNL = Ui - Ui, (рис. 4).
Рис. 4. Определение интегральной нелинейности
Время преобразования Т
пр обычно определяется как интервал времени от начала преобразования до появления на выходе АЦП устойчивого кода. Для одних АЦП это время постоянное и не зависит от входного сигнала, для других зависит. Если АЦП работает без устройства выборки и хранения, то время преобразования является апертурным временем.
Максимальная частота дискретизации - частота, с которой возможно преобразование входного сигнала, при условии, что выбранный параметр не выходит за заданные пределы. Иногда максимальную частоту преобразования принимают равной обратной величине времени преобразования.
Принципы построения АЦП
АЩП мгновенных значений подразделяют на следующие основные виды: последовательного счета, последовательного приближения, параллельные, параллельно-последовательные и с промежуточным преобразованием в интервале времени. Структурная схема АЦП последовательного счета (рис. 5) содержит компаратор, при помощи которого выполняется сравнение входного напряжения с напряжением обратной связи. На прямой вход компаратора поступает входной сигнал Uвх, а на инвертирующий - напряжение обратной связи. Работа преобразователя начинается с приходом импульса «ПУСК» от схемы управления, который замыкает ключ S. Через замкнутый ключ S импульсы U1 от генератора тактовых импульсов поступают на счетчик, который управляет работой цифро-аналогового преобразователи (ЦАП). В результате последовательного увеличения выходного кода счетчика N происходит последовательно-ступенчатое увеличение выходного напряжения U5 ЦАП. Когда выходное напряжение ЦАП сравняется с входным напряжением, произойдет переключение компаратора, и по его выходному сигналу «СТОП» разомкнется ключ S. В, результате импульсы от генератора перестанут поступать на вход счетчика. Выходной код, соответствующий равенству Uвх=Us, снимается с выходного регистра счетчика.
Графики, иллюстрирующие процесс преобразования напряжения в цифровой код, приведены на рис. б. Из этих графиков следует, что время преобразования зависит отуровни входного напряжения. При числе двоичных разрядов счетчика, равном n, и периоде следования счётных импульсов Т максимальное время преобразования можно определить по формуле
Тпр = (2n – 1)Т.
Уравнение преобразования АЦП последовательного счета можно записать в виде
КU = Uвх,
где 0 Кn – число ступеней до момента сравнения;
U – шаг квантования.
Структурная схема АЦП последовательного приближения (рис. 7) отличается от структурной схемы последовательного счета тем, что вместо счетчика импульсов включен регистр последовательных приближений РПП.
В основе РПП лежит принцип дихотомии, т.е. последовательного сравнения преобразуемого напряжения Uвх с ½, ¼, 1/8 и т.д. возможного максимального его значения Um. Это позволяет для n - разрядного АЦП выполнить весь процесс преобразования за п последовательных шагов (итераций) вместо (2n-1) при использовании последовательного счета и получить существенный выигрыш по быстродействию.
Рис. 5. Структурная схема АЦП последовательного счета
На рис. 7 приведена структурная схема, реализующая метод последовательных приближений. На каждом шаге производится определение одного разряда, начиная со старшего. При первом сравнении определяется, больше или меньше напряжение Uвх, чем Um/2. На следующем шаге определяется, в какой четверти диапазона находится Uвх. Каждый последующий шаг сужает область возможного результата. При каждом сравнении компаратор формирует импульсы, соответствующие состоянию «больше - меньше» (1 или 0), управляющие регистром последовательных приближений.
Рис. 6. Временные диаграммы процесса последовательного счета
График процесса последовательного приближения приведен на рис. 8.
Структурная схема параллельного АЦП приведена на рис. 9. Преобразователь осуществляет одновременное квантование входного сигнала Uвх с помощью компараторов, включенных параллельно входному сигналу. Пороговые уровни компараторов установлены с помощью резистивного деления в соответствии с используемой шкалой квантования. На выходах компараторов получаем квантованный сигнал, представленный в унитарном коде.