Добавлен: 09.11.2023
Просмотров: 18
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| | 3 | 0 | 0 |
| А= | 2 | 7 | -4 |
| | 2 | -2 |  5 5 |
Задача 1
1.Из определения собственного вектора v соответствующего собственному значению λ: Av=λv
Тогда:Av−λv=(A−λE)⋅v =0
Уравнение имеет ненулевое решение тогда и только тогда, когда det(A−λE)=0
| | 3-λ | 0 | 0 | |
| det(A−λE) = | 2 | 7-λ | -4 | = - 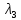 +15 +15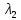 −63λ+81=−(λ−9)⋅( −63λ+81=−(λ−9)⋅(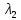 −6λ+9)=−(λ−9)⋅(λ−3)2=0; −6λ+9)=−(λ−9)⋅(λ−3)2=0; |
| | 2 | -2 | 5-λ | |
Тогда:
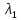 =9;
=9; 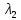 =3.
=3.2.Для каждого λ найдем его собственные вектора:
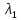 =9
=9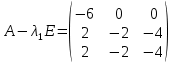 ;
;Av=λv ;
(A−λE)⋅v=0;
Тогда имеем однородную систему линейных уравнений, решим ее методом Гаусса:
| -6 | 0 | 0 |  0 0 |
| 2 | -2 | -4 | 0 |
| 2 | -2 | -2 | 0 |
| 1 | 0 | 0 |  0 0 |
| 0 | 1 | 2 | 0 |
| 0 | 0 | 0 | 0 |
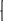
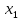 =0; =0; |
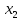 + +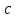 =0. =0.Из уравнения 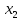 + +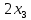 =0 найдем переменную =0 найдем переменную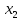 : :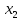 = =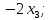 Из уравнения 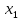 =0 найдем переменную =0 найдем переменную 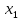 : :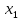 =0; =0;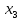 = =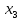 . .Ответ: :  =9; =9;  =3; =3;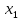 =0; =0;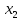 = =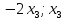 = =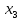 . .Задача 2 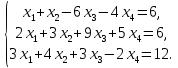 Решение: Метод Гауса Запишем систему уравнений в виде расширенной матрицы: 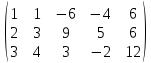 → →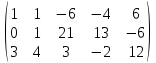 → →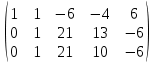 → →→ 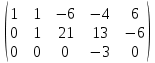 Получим систему: Получим систему: 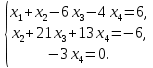 Решим уравнение  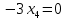 найдем перменнную найдем перменнную 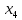 : :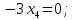 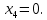 Решим уравнение 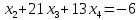 найдем найдем 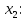 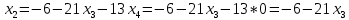 Решим уравнение 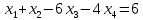 найдем найдем 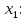 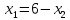 + +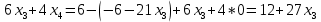 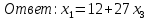 ; ;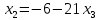 ; ; 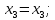 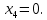 Даную систему уравнений невозможно решить методом Крамерра или средствами матричного исчесления т.к. полученаая из системы уравнений расширеная матрица не квадратная. Задача3  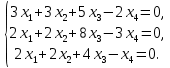 Запишем систему уравнений в виде расширенной матрицы и решим методом Гаусса: 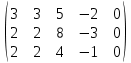 → →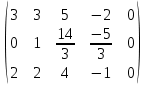 → →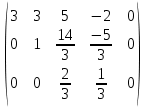 из этого получим систему: 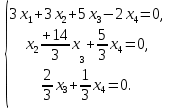 Найдем переменную 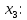 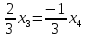 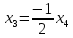 Найдем переменную 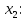 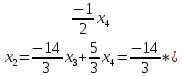 ) )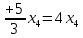 Найдем переменную 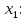 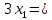 - -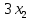 - -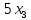 + +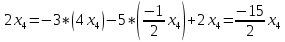 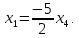 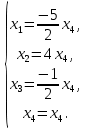 общее решение. общее решение.Ответ: 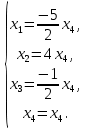 Векторная алгебра Задача 1 Найдем значение вектора 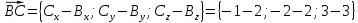 = =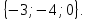 Используя формулу: 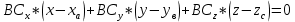 составим уравнение плоскости P: 4*(x+3)-3*(y+4)-2*(z-0)=0; составим уравнение плоскости P: 4*(x+3)-3*(y+4)-2*(z-0)=0;4x-3y-2z=0. Найдем нормерующий множитель используя формулу: 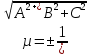 , где А=4; В=3; С=2. , где А=4; В=3; С=2.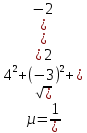 Умножим обе части общего уравнения плоскости на 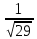 получим нармальное уравнение плоскости: получим нармальное уравнение плоскости: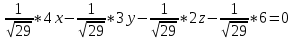 ; ;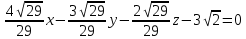 ; ;Найдем уравнение плоскости в отрезках используя уравнение плоскости в отроезках: 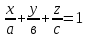 ,где ,где 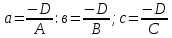 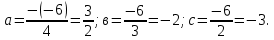 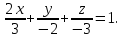 Найдем уравнение плоскости 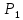 используя формулу: используя формулу: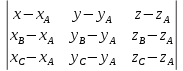 =0, =0,Подставим данные и упростим выражение 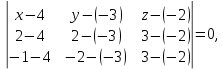 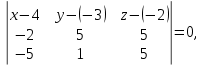 (x-4)*(5*5-5*1)-( 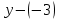 )*(-2*5-5*(-5)+( )*(-2*5-5*(-5)+(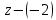 )*(-2*1-5*(-5))=0, )*(-2*1-5*(-5))=0,20x-15y+23z-79=0. Вычислим угол между плоскостью Р и 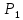 : :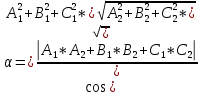 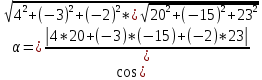 = = 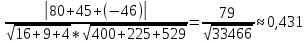 α≈64.4̊ Для вычисления расстояния от точки D 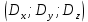 до плоскости до плоскости 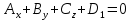 используем формулу: используем формулу: 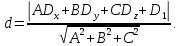 Подставим данные,получим: 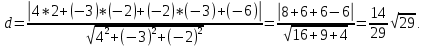 Ответ: 4x-3y-2z=0; 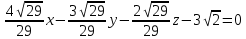 ; ; 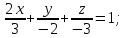 20x-15y+23z-79=0; α≈64.4̊; 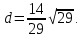 Задача 2 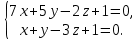 Запишем формулу кононического уравнения прямой l: 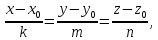 где k,m,n координаты колониарного вектора прямой l т.е. где k,m,n координаты колониарного вектора прямой l т.е.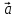 ||l; ||l;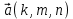 . .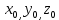 координаты некоторой точки К пренодлежащей прямой l:К( координаты некоторой точки К пренодлежащей прямой l:К(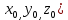 . .Исходя из системы уравнений заданной прямой можем записать координаты нармальных векторов 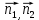 : : 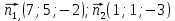 Обозначим плоскость 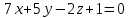 через α, а плоскость через α, а плоскость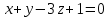 через β. через β.Найдем координаты вектора 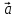 : :Т.к. 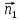 ﬩ α → ﬩ α → 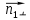 l,a l,a 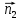 ﬩ β → ﬩ β → 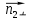 l из этого следует что векторное произведение векторов l из этого следует что векторное произведение векторов 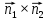 пароллельно l, из этого следует, что пароллельно l, из этого следует, что 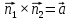 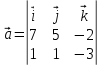 = = 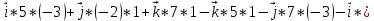 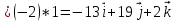 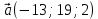 Найдем координаты точки К: Пусть y=0 тогда: 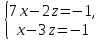 выразим из нижнего уравнения x и подставим его значение в верхнее уравнение получим что : выразим из нижнего уравнения x и подставим его значение в верхнее уравнение получим что : 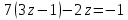 ; z= ; z=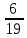 x= x=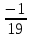 K ( 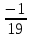 ;0; ;0;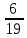 ) )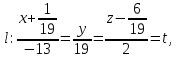 кононическое уравнение. кононическое уравнение.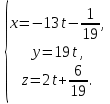 параметрическое уравнение. параметрическое уравнение.Т.к. точка М имеет координаты: М(2;0;3),а кононическое уравнение прямой l: 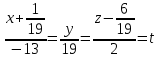 ,а прямая ,а прямая 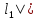 l то у них будет общий направляющий вектор l то у них будет общий направляющий вектор 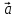 с координатами с координатами 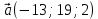 . Тогда используя кононическое уравнение прямой . Тогда используя кононическое уравнение прямой 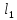 ; ;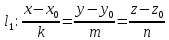 получим: получим: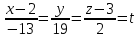 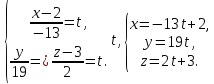 Используя кононическое уравнение прямой 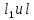 координаты точки М(2;0;3), координаты некоторая точка К принадлежащая прямой координаты точки М(2;0;3), координаты некоторая точка К принадлежащая прямой 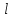 с координатами К( с координатами К(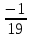 ;0; ;0;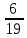 ), координаты направляющего вектора ), координаты направляющего вектора 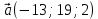 и обозначив ростояние между прямыми и обозначив ростояние между прямыми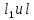 , как МН. Найдем длину , как МН. Найдем длину 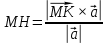 где где 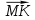 =(- =(-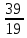 ;0;- ;0;-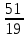 ) )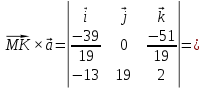 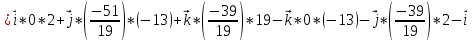 * *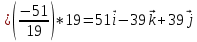 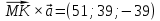 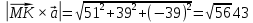 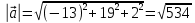 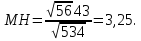 Прямая 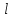 заданна через систему заданна через систему 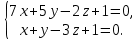 Точкка М имеет координаты : М(2;0;3) Через заданную точку проведем плоскость Q перпендикулярно данной прямой. Тогда точка пересечения будет являтся искомой проекцией. Состовляем уравнение плоскости проходящей через точку М(2;0;3) перпендикулярно прямой l. Зная координаты направляющего вектора 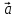 , и т.к.l , и т.к.l 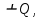 то то 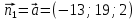 Используя уравнение плоскости проходящей через точку, перпендикулярно прямой 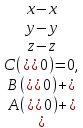 запишем уравнение плоскости Q: запишем уравнение плоскости Q:-13(x+ 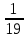 )+19y+2(z- )+19y+2(z-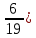 =0, =0,-13x+9y+2z- 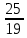 =0. =0.Обозначим точку пересечения прямой l и плоскости Q через S,и найдем ее координаты. Запишем параметрическое уравнение прямой l. 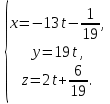 Подстовляем значения неизвесных в уравнение плоскости Q получим: 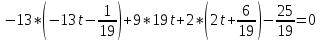 , ,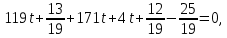 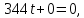 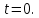 Подстовляем значения t в параметрическое уравнение прямой: 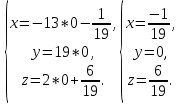 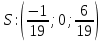 . .Используя уравнение плоскости Р: 2x-5y-2z-6=0 можем записать координаты нармального вектора 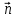 (2;-5;-2), а из кононического уравнения прямой l координаты направляющего вектора (2;-5;-2), а из кононического уравнения прямой l координаты направляющего вектора 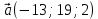 и координаты точки K ( и координаты точки K (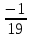 ;0; ;0;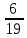 ) пренодлежащей прямой l. Запишем уравнение прямой l в параметрическом виде: ) пренодлежащей прямой l. Запишем уравнение прямой l в параметрическом виде: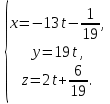 К параметрическому уравнению прямой добовляем уравнение плоскости P и решаем полученную систему: 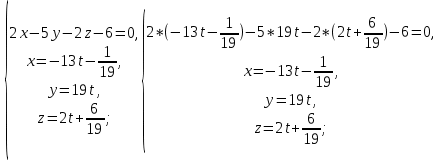 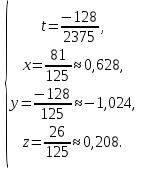 Пусть А точка пересечения плоскости Р и прямой 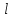 тогда ее координаты равны: тогда ее координаты равны:А(0,648;-1,024;0,208). Ответ: 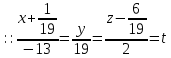 ; ;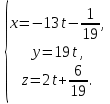 ; ;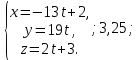 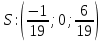 ; А(0,648;-1,024;0,208). ; А(0,648;-1,024;0,208).Аналогическая геометрия Задача 1 A(1;2) B(3;4) C(-1;2) Используя формулу уравнений сторон треугольника по координатам его вершин составим уравнения сторон АВ,АС,ВС : AB: 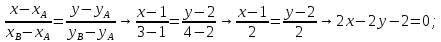 AC: 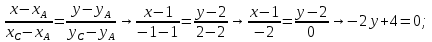 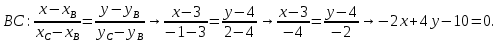 Обозначим медиану угла А как отрезок А 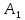 где координаты точки А известны по условию, а координаты точки где координаты точки А известны по условию, а координаты точки 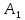 найдем по формуле определения координат середины отрезка: найдем по формуле определения координат середины отрезка: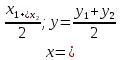 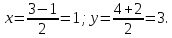  Используя формулу уравнения медиана по координатам вершин треугольника составим уравнение медианы А Используя формулу уравнения медиана по координатам вершин треугольника составим уравнение медианы А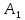 : :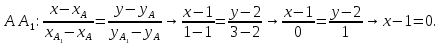 Используя формулу определения длины медиана по координатам вершин треугольника найдем длину медианы А 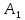 : :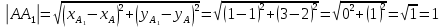 Исходя из уравнения стороны ВС: 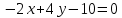 угловой коофициент ВС равен угловой коофициент ВС равен 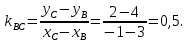 Т.к. прямые ВС и 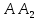 перпендикулярны,то, зная угловой коофициент ВС, можем составить уравнение высоты перпендикулярны,то, зная угловой коофициент ВС, можем составить уравнение высоты 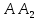 : :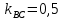 Отсюда угловой коофициент 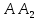 будет равен: будет равен: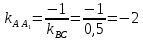 Можем записать уравнение высоты Можем записать уравнение высоты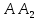 : :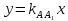 + +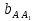 отсюда y=-2x+ отсюда y=-2x+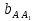 Точка А лежит на прямой 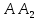 значит ее координаты удовлетворяют уравнению прямой значит ее координаты удовлетворяют уравнению прямой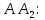 2=-2*1+ 2=-2*1+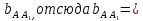 4. 4.Таким образом уравнение высоты 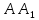 имеет вид: имеет вид:-2x-y+4=0. Используя формулу определения длины высоты по координатам вершин треугольника найдем длину высоты 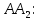 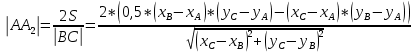 = =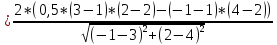 = =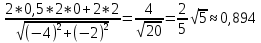 Обозначим точку пересечения биссектриса угла А и стороны ВС как 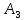 . Тогда, так как биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон (теорема о биссектрисе), и используя формулы для нахождения координат точки, делящей отрезок в данном отношении, имеем: . Тогда, так как биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон (теорема о биссектрисе), и используя формулы для нахождения координат точки, делящей отрезок в данном отношении, имеем: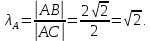 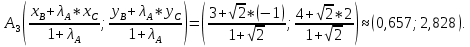 Используя формулу прямой по двум точкам составим уравнение биссектриссы угла А 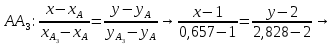 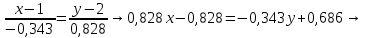 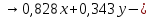 1,514=0. 1,514=0. |
Используя формулу определения длины биссектрисы по координатам вершин треугольника найдем длину биссектрисы
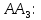
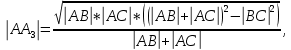 где
где 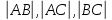 длины сторон AB, AC, BC
длины сторон AB, AC, BC 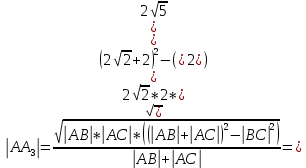
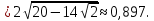
Используя формулу для состовления уравнений прямых проходящих через вершины треугольника и поролельных его сторонам по координатам вершин треугольника составим уравнения прямых А,В,С.
С пароллельна AB:
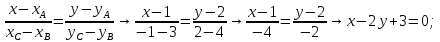
В пароллельна AC:
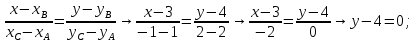
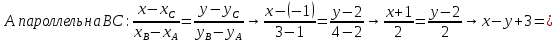
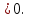
Ответ:
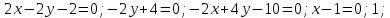
-2x-y+4=0;
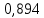 ;
;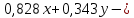 1,514=0;
1,514=0;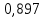 ;
;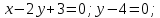
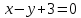 .
.Задоча 2
А(2;0;3) B(1;0;7) C(0;1;3) D(2;2;4)
Найдем длины ребер АВ и АС:
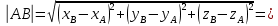
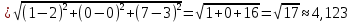 ;
;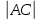 =
=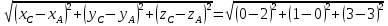 =
==
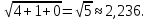
Вычислим угол между ребрами АВ и АС по теореме косинусов:
Угол(АВ,АС)=
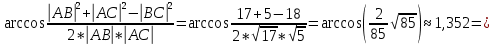
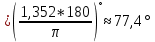 .
.Вычислим площадь грани АВС:
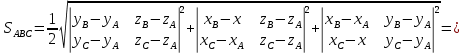
=
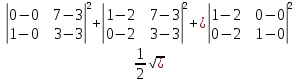 =
=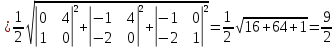 =4,5.
=4,5.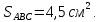
Найдем проекцию вектора
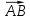 на вектор
на вектор 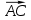 по формуле:
по формуле:Пр
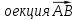 на
на 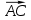 =
=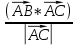 =
=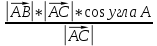 =
=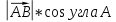
Угол А приблезительно равен
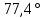 , смотри выше по решению. Найдем длину вектора
, смотри выше по решению. Найдем длину вектора 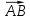
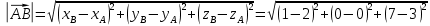 =
=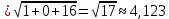 .
.Таким образом пр
 на
на  равна
равна 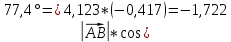 .
.Найдем обем пирамиды ABCD:
V=
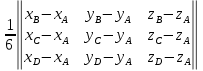 =
=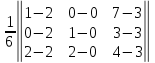 =
=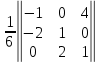 =
=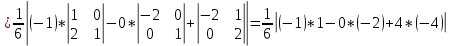 =
=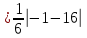 =
=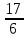 =2,833.
=2,833.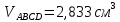 .
.Ответ: