Файл: Новосибирский государственный технический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 18
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Расчётно-графическая работа
Моделирование случайных чисел с заданным законом распределения.
Проверка гипотез
Выполнили: (Бригада 2):
Ганиев Роман
Дмитриев Николай
Поздняков Никита
Группа: АВТ-212
Преподаватель: Ландовский В.В.
НОВОСИБИРСК
2023
Задание
Разработать программу, позволяющую:
- получать случайные числа с заданным законом распределения заданным методом;
- для полученной выборки (одной или двух в зависимости от варианта) строить гистограмму;
- заданным критерием проверять гипотезу о том, что полученную выборку действительно можно считать распределенной исходному закону (проверить качество случайных чисел). В некоторых вариантах проверить, что две выборки имеют один закон (гипотеза об однородности выборок).
Закон распределения: f(x) = -0,5x + 1,5 на интервале (1;3), метод усечения, критерий Колмогорова, выборка одна, проверка гипотезы о совпадении выборочного распределения с теоретическим.
Описание используемых алгоритмов
-
Генерация выборки объёмом N (задаётся пользователем) числами в диапазоне [0, 1]. Сгенерированные числа растягиваются на заданный интервал (1, 3) путем умножения числа на длину интервала и +1. -
Методом усечения при генерации выборки будут выбираться числа, которые находятся ниже значения заданной функции в данном интервале и попадающие в этот интервал (предварительно пользователь задаёт K интервалов). Таким образом будет сгенерирован массив случайных чисел с данным законом распределения. -
Далее в выборке подсчитываются точки в каждом интервале и строится гистограмма, отображающая распределение. -
Проверка гипотезы о совпадении выборочного распределения с теоретическим по критерию Колмогорова заключается в том, что сравнивается максимум модуля разности эмпирической и теоретической функций распределения. Для этого в процессе подсчёта точек в интервалах, сохраняется их количество в массиве, откуда потом берётся максимальное значение, из которого вычитается максимальное значение теоретической функции. -
П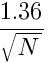
оученное значения сравнивается с критическим значением, которое высчитывается по формуле: .
Полученные результаты
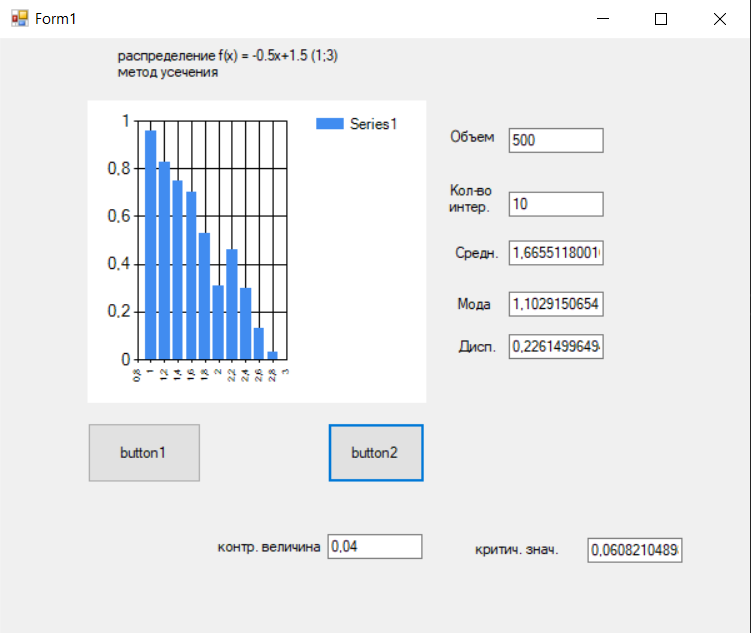
Сгенерирована выборка, содержащая 500 значений, подходящих под закон распределения. Критическое значение - 0,06; контрольная величина – 0,04, далее необходимо интерпретировать полученные результаты.
В тесте Колмогорова используются две гипотезы:
-
Нулевая H 0; -
Альтернативная H A;
Чтобы определить должна ли отклоняться нулевая гипотеза следует обратиться к контрольной величине она получилась 0,04 по формуле заданной в п.5 описания алгоритмов находим критическое значение, которое равно 0,06. Получается, что контрольная величина не превышает критического значения, следовательно, мы не можем отвергнуть гипотезу H 0. Это означает, что мы можем предположить, что наше выборочное распределение соответствует теоретическому.
Текст программы
| using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using System.Threading; using System.Threading.Tasks; using System.Windows.Forms; namespace WindowsFormsApp1 { public partial class Form1 : Form { double[] arr; double[] rasp_arr; int N, K; double f(double x) { double y = -0.5 * x + 1.5; return y; } public Form1() { InitializeComponent(); } private void Form1_Load(object sender, EventArgs e) { } private void chart1_Click(object sender, EventArgs e) { } private void button2_Click(object sender, EventArgs e) { double G = N; chart1.Series[0].Points.Clear(); N = Convert.ToInt32(textBox1.Text); K = Convert.ToInt32(textBox2.Text); rasp_arr = new double[K]; int count = 0; for (int i = 0; i < K; i++) { double left = 1 + 0.2 * i; double right = 1 + 0.2 * (i + 1); for (int j = 0; j < N; j++) { if ((arr[j] >= left) && (arr[j] <= right)) { count++; } } chart1.Series[0].Points.AddXY(left, count/(N * 0.2)); rasp_arr[i] = count / (N * 0.2); count = 0; } double sum = arr.Sum(); double sr = sum / N; textBox3.Text = String.Format("{0}", sr); double num = arr[0]; int max_frq = 1; int frq; for(int i = 0; i < N - 1; i++) { frq = 1; for(int k = i+1; k < N; k++) { if (arr[i] == arr[k]) { frq += 1; } } if(frq > max_frq) { max_frq = frq; num = arr[i]; } } textBox4.Text = String.Format("{0}", num); double disp; double sr_kv = 0; for (int i = 0; i < N; i++) { sr_kv = sr_kv + Math.Pow((arr[i] - sr), 2); } disp = sr_kv / (N - 1); textBox5.Text = String.Format("{0}", disp); double krit = 1.36 / Math.Sqrt(N); double exp_max = f(1); double ctrl = Math.Abs(rasp_arr.Max() - exp_max); textBox6.Text = String.Format("{0}", ctrl); textBox7.Text = String.Format("{0}", krit); } private void label1_Click(object sender, EventArgs e) { } private void label3_Click(object sender, EventArgs e) { } private void label7_Click(object sender, EventArgs e) { } private void label8_Click(object sender, EventArgs e) { } private void button1_Click(object sender, EventArgs e) { N = Convert.ToInt32(textBox1.Text); K = Convert.ToInt32(textBox2.Text); double f(double x) { double y = -0.5 * x + 1.5; return y; } Random a = new Random(); double r1; double rx; double ry; arr = new double[N]; for (int i = 0; i < N; i++) { r1 = a.NextDouble(); ry = a.NextDouble(); rx = r1 * 2 + 1; while (ry > f(rx)) { r1 = a.NextDouble(); ry = a.NextDouble(); rx = r1 * 2 + 1; } arr[i] = rx; } } } } |