Файл: Тема 1. Первинна обробка статистичних даних. Графічні методи аналізу. Описова статистика. Перевірка нормального розподілу.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема №1. Первинна обробка статистичних даних. Графічні методи аналізу. Описова статистика. Перевірка нормального розподілу.
Побудова варіаційних і інтервальних рядів. Елементи та характеристики варіаційних рядів.
Графічні методи аналізу даних. Типи діаграми (лінійні, стовпчикові, внутрішньостовпикові, секторні, радіальна, картограми і картодіаграми), правила їх побудови, правильне використання.
Середні значення: їх види, методи розбору, особливості використання. Медіана та мода.
Поняття варіації, її значення ‑ зміна сукупних параметрів, оцінювання методів: індикатори абсолютної варіації (амплітуда, середнє квадратичне значення) та індикатори відносної варіації (варіації та визначення коефіцієнтів), їх оцінка міри варіації, концепція законів розподілу, їх типи, характеристики.
Оцінка нормально розподілу, «вискакуючі» варіанти. Правило сигм, його практичне використання.
Таблиця 1.
| Варіант № | Дані |
| 1 | 9, 13, 9, 6, 9, 9, 13, 10, 7, 10, 5, 11, 11, 11, 10, 12, 14, 11, 11, 9, 9 |
| 2 | 19, 19, 13, 19, 19, 9, 13, 12, 17, 15, 13, 17, 19, 14, 12, 16, 18, 15, 15, 12, 13 |
| 3 | 17, 14, 18, 17, 18, 17, 20, 15, 19, 22, 23, 21, 27, 20, 20, 11, 15, 21, 21, 16, 19 |
| 4 | 7, 6, 7, 9, 9, 14, 7, 9, 8, 9, 13, 12, 11, 10, 12, 8, 13, 10, 11, 8, 12 |
| 5 | 18, 12, 18, 15, 17, 6, 10, 16, 16, 20, 17, 15, 16, 10, 17, 14, 18, 16, 16, 21, 17 |
| 6 | 17, 11, 13, 21, 24, 15, 15, 17, 15, 17, 19, 22, 13, 23, 16, 19, 20, 15, 16, 24, 19 |
| 7 | 10, 10, 6, 9, 13, 12, 11, 11, 7, 14, 7, 11, 8, 8, 12, 7, 13, 8, 10, 8, 11 |
| 8 | 14, 16, 17, 15, 13, 15, 12, 13, 16, 15, 19, 18, 22, 17, 17, 15, 11, 19, 14, 15, 7 |
| 9 | 25, 18, 14, 20, 17, 15, 23, 18, 12, 20, 18, 20, 20, 15, 21, 19, 11, 16, 25, 20, 25 |
| 10 | 13, 12, 8, 10, 10, 15, 12, 9, 9, 7, 9, 7, 10, 14, 9, 11, 10, 6, 8, 9, 9 |
| 11 | 19, 16, 12, 13, 9, 18, 13, 16, 10, 14, 15, 14, 12, 23, 16, 17, 14, 10, 13, 18, 11 |
| 12 | 15, 16, 21, 20, 16, 16, 18, 20, 20, 11, 22, 17, 20, 17, 19, 17, 20, 13, 24, 21, 14 |
| 13 | 12, 8, 9, 8, 10, 9, 14, 12, 10, 9, 12, 8, 10, 11, 8, 11, 10, 12, 12, 9, 13 |
| 14 | 16, 14, 11, 16, 16, 13, 16, 13, 19, 19, 16, 17, 15, 15, 17, 11, 8, 14, 12, 15, 17 |
| 15 | 18, 20, 11, 14, 20, 13, 20, 15, 20, 19, 16, 25, 15, 25, 19, 21, 15, 17, 16, 20, 12 |
Дані для прикладу: 11, 9, 8, 9, 9, 10, 13, 13, 9, 10, 11, 9, 9, 12, 7, 12, 9, 13, 11, 10, 14
Якщо ми впорядкуємо ці дані за зростанням, то отримаємо варіаційний ряд:
7, 8, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12, 12, 13, 13, 13, 14
В цьому ряді перше значення буде мінімальним, а останнє ‑ максимальним. Різниця між цими значеннями називається розмахом ряду.
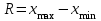
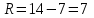
Далі з варіаційного ряду будувємо інтервальний ряд у вигляді таблиці (табл. 2). Якщо бажаємо отримати 5 інтервалів, треба розмах поділити на 5: 7: 5 = 1,4.
Таблиця 2.
| Границі інтервалів | 7 – 8,4 | 8,5 ‑ 9,8 | 9,9 – 11,2 | 11,3 ‑ 12,6 | 12,7 ‑ 14 |
| Частота | 2 | 7 | 6 | 2 | 4 |
На основі інтервального ряду побудуємо гістограму – кожному інтервалу відповідає стовпчик, висота якого дорівнює частоті (рис. 1).
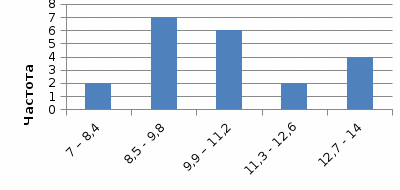
Рис. 1. Гістограма розподілу
Для порівняння лінійна діаграма (багатокутник):
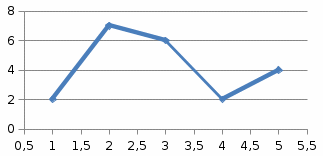
Рис. 2. Лінійна діаграма
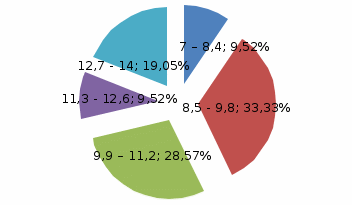
Рис. 3. Секторна діаграма
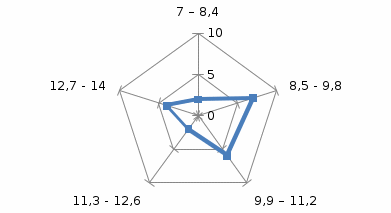
Рис. 4. Радіальна діаграма
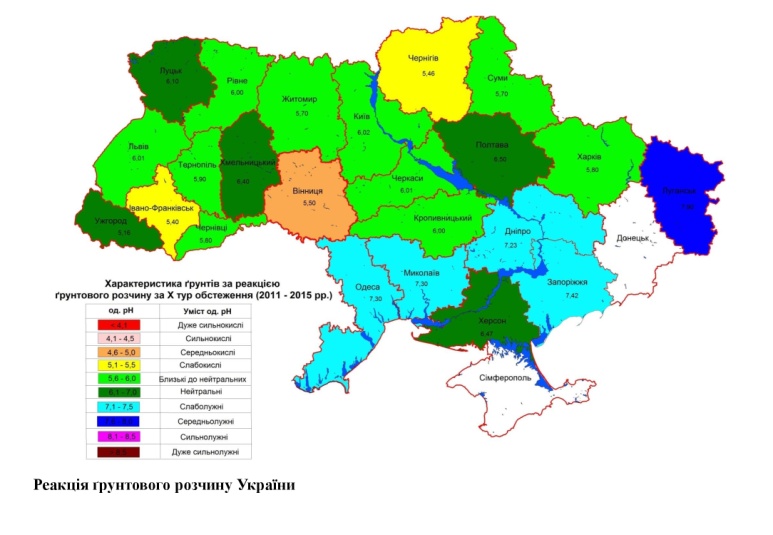
Рис. 5. Картограма
У лекції 1: весь розподіл даних можна охарактеризувати одним типом групування, який представляє всі показники центру групування. До показників центру групування відносяться вибіркове середнє, медіана, мода.
Мода – значення ознаки, яке в вибірці зустрічається найбільшу кількість разів. Відповідає на графічному зображенні максимальної ординаті, тобто найвищому значенню графічної кривої. Мода позначається Mо. Мода не залежить від крайніх варіант або від ступеня розсіювання ряду.
7, 8, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12, 12, 13, 13, 13, 14
У нашому прикладі це Mо=9
Медіана – це середина, центральна варіанта, що ділить варіаційний ряд на дві рівні частини. Коли розподіл має непарну кількість спостережень, то медіана дорівнює середньому значенню; коли вона має парну кількість спостережень, то центральне положення мають дві величини (тобто це середнє значення або півсума двох середніх балів).
7, 8, 9, 9, 9, 9, 9, 9, 9, 10, 10, 10, 11, 11, 11, 12, 12, 13, 13, 13, 14
У нашому прикладі це Ме=10
Вибіркове середнє визначається як сума варіант варіаційного ряду, поділена на їх число. Він позначається µ ряду елементів («x-bar») у вибірці. Отже, формули для обчислення середнього значення
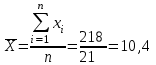
Існує три основних показника варіації: розмах, дисперсія та середньоквадратичне відхилення.
Розмах ряду:


Д
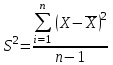 исперсія – це середній квадрат відхилень спостережень від вибіркового середнього.
исперсія – це середній квадрат відхилень спостережень від вибіркового середнього.Таблиця 3.
| X | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Частота mi | 1 | 1 | 7 | 3 | 3 | 2 | 3 | 1 |
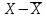 | -3,4 | -2,4 | -1,4 | -0,4 | 0,6 | 1,6 | 2,6 | 3,6 |
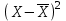 | 11,56 | 5,76 | 1,96 | 0,16 | 0,36 | 2,56 | 6,76 | 12,96 |
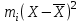 | 11,56 | 5,76 | 13,72 | 0,48 | 1,08 | 5,12 | 20,28 | 12,96 |
11,56+5,76+13,72+0,48+1,08+5,12+20,28+12,96=70,96
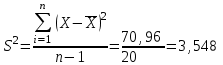
Середньоквадратичне відхилення є коренем квадратним з дисперсії, тому воно виражається в тих же одиницях, що основні варіанти.
S=SD=1,88
Коефіцієнт варіації – середньоквадратичне відхилення, поділене на вибіркове середнє і виражене у відсотках.
V = 1,88 / 10,4 * 100% = 18,08%
Для розрахунку усіх цих показників ми будемо використовувати MS Excel. Виберіть «Дані», потім «Аналіз даних» (рис. 6).

Рис. 6.
На вкладці «Аналіз даних» виберіть «Описова статистика» (рис. 7).
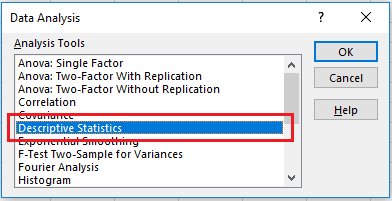
Рис. 7. Описова статистика в MS Excel.
У відкритому вікні введіть дані, щоб вказати інтервал вивода, відмітьте «Зведена таблиця» та «Рівень достовірності для середнього», як показано на рис.8. Натисніть кнопку ОК.
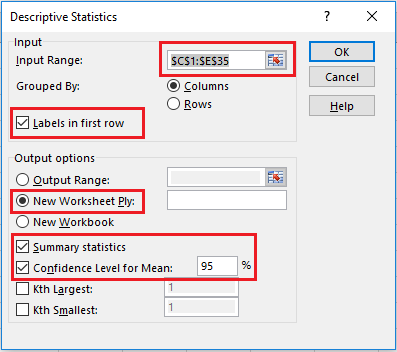
Рис. 8.
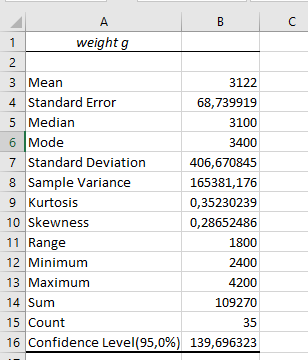
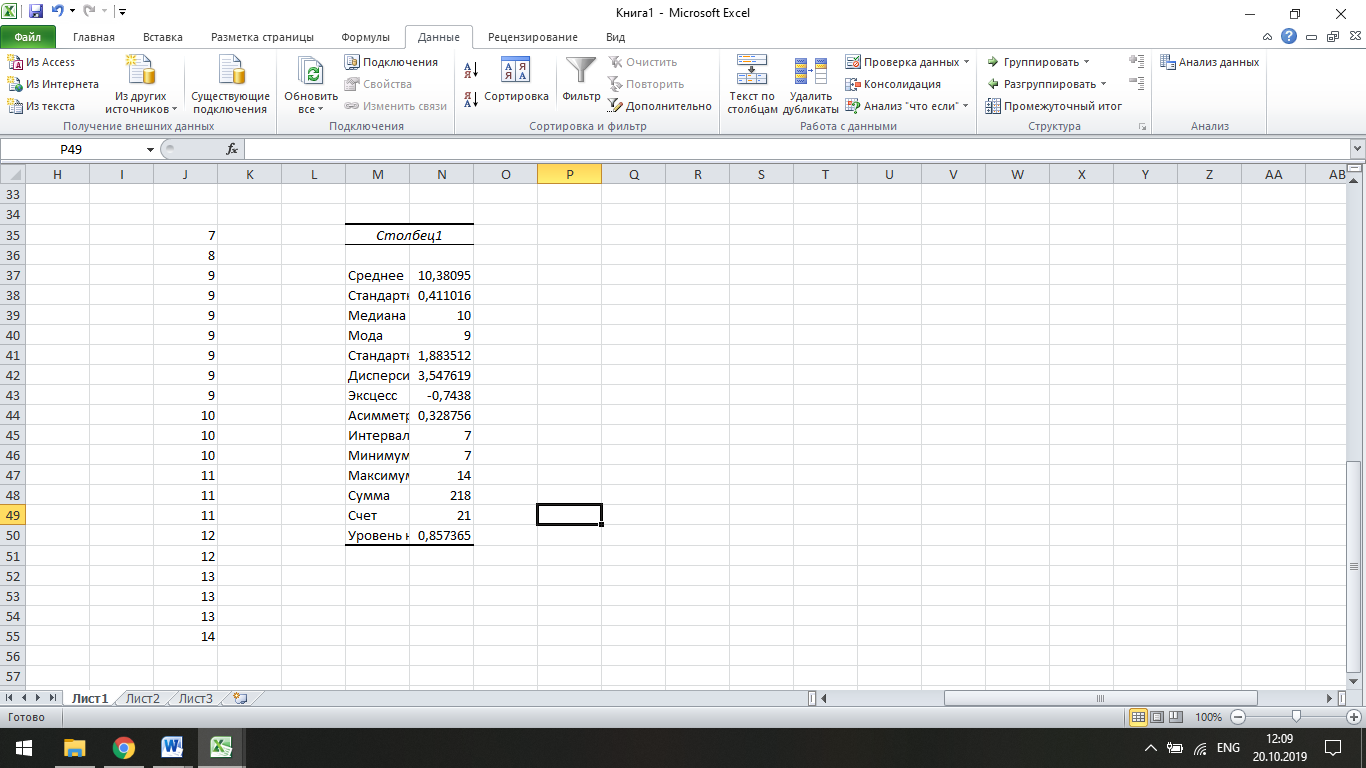
Рис. 9. Результат команди Descriptive Statistics
Співвідношення між трьома показниками центру групування залежить від типу розподілу. В одномодальному симетричному розподілу (нормальний розподіл) усі три показника ідентичні, але в інших випадках вони розрізняються.
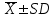 8,52 – 12,28 (9, 10, 11, 12) 15/21*100=71,4% (68%)
8,52 – 12,28 (9, 10, 11, 12) 15/21*100=71,4% (68%)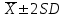 6,64 – 14,16 100% (95%)
6,64 – 14,16 100% (95%)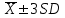 4,76 - 16,04
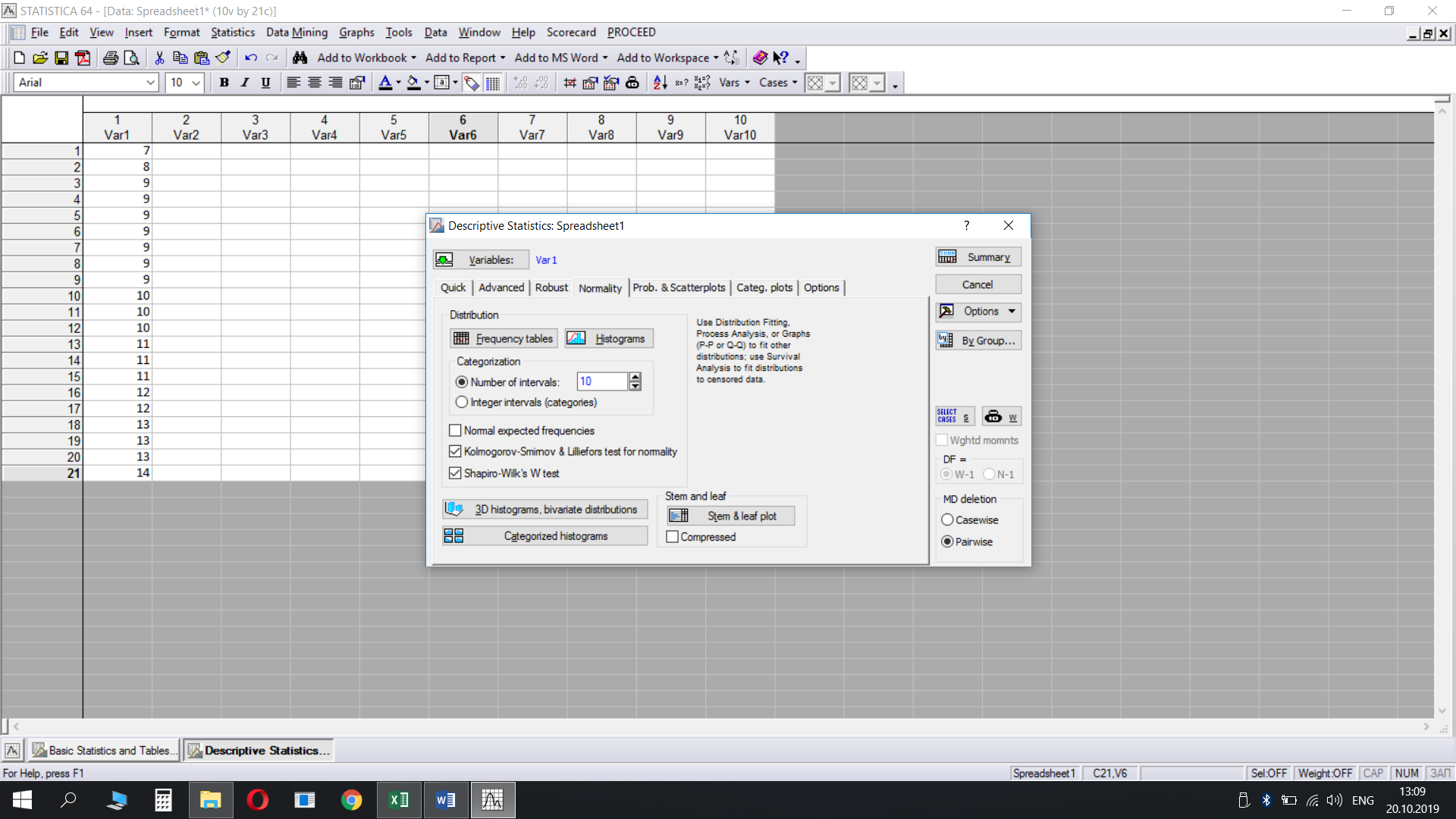
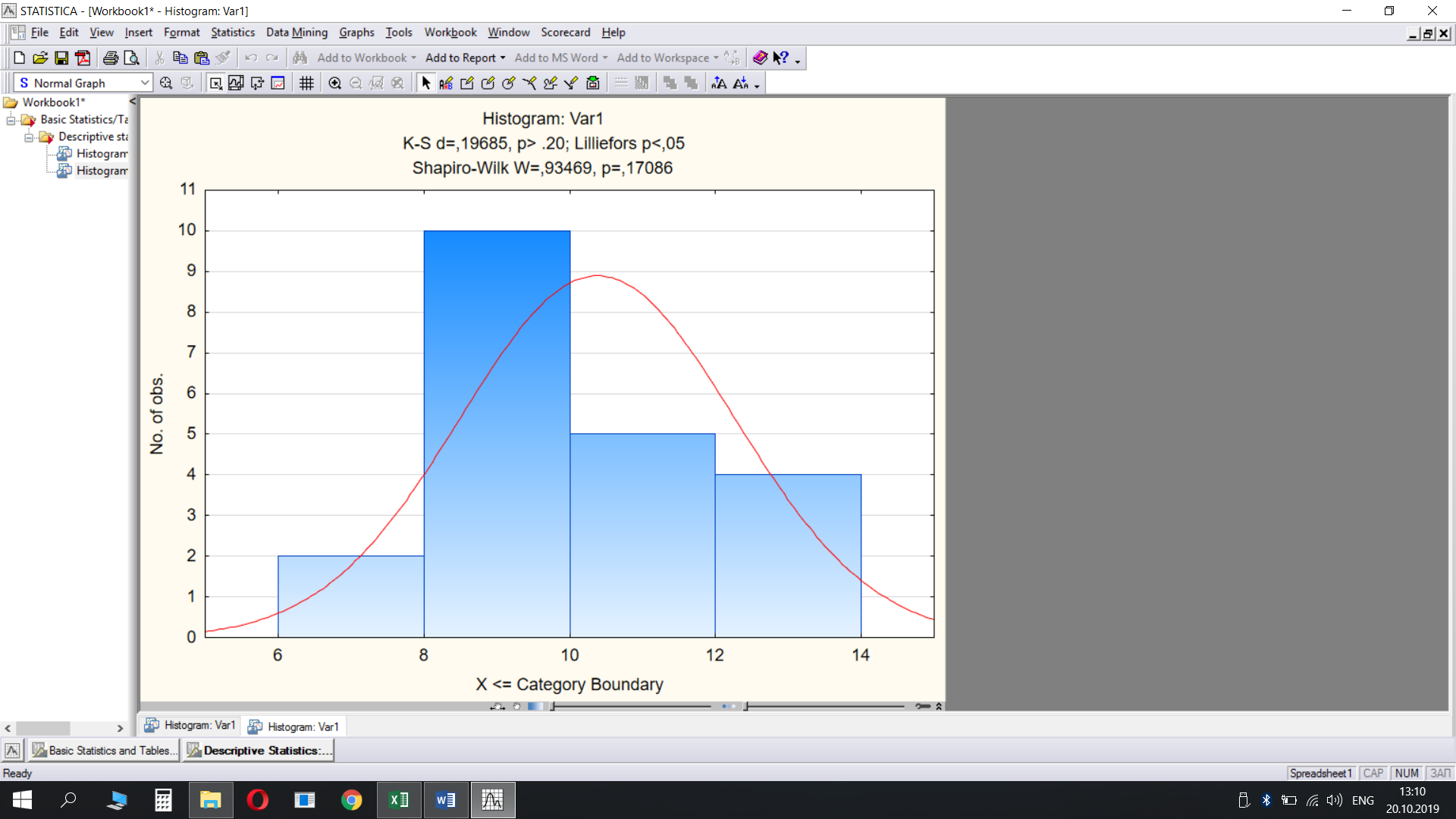
4,76 - 16,04Перевірку зручно робити в спеціальних статистичних програмах, наприклад, в програмі Statistica.