Полупроницаемые – породы, проницаемость которых находится в пределах от 10^-4 до 10^-2 мкм². Это глинистые пески, некоторые песчаники и алевролиты, мелкотрещиноватые известняки и доломиты. Большую часть этих пород занимают субкапиллярные поры.

Практически непроницаемыми считаются породы с коэффициентами проницаемости менее 10^-4 мкм². К таким породам относятся глины, аргиллиты, глинистые сланцы, плотносцементированные песчаники и алевролиты с субкапиллярными порами, плотные карбонатные, магматические и метаморфические породы.

16. 
    Линейный закон фильтрации (закон Дарси).
    

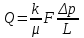. (1.4.6)

Здесь Q - объемный расход жидкости в единицу времени; - скорость линейной фильтрации; F - площадь фильтрации; 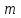- динамическая вязкость жидкости; 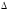Р - перепад давления; L - длина пористой среды; k – коэффициент проницаемости или пропускной способности среды:

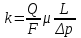(1.4.7)

Размерность k в системе СИ[k]=м².

Таким образом, физический смысл проницаемости можно объяснить пропускной способностью породы, а именно той площадью поперечного сечения, которое способно пропустить через себя жидкость или газ.

Уравнение (1.4.7) можно переписать следующим образом:

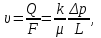
(1.4.8)

Здесь - скорость фильтрации жидкости в пористой среде, которая в соответствии с уравнением (1.4.8) пропорциональна градиенту давления и обратно пропорциональна динамической вязкости:

Итак, в международной системе СИ за единицу проницаемости в 1м²

---

принимается проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 м² и длиной 1 м при перепаде давления 1 Па расход жидкости составляет 1 м³/сек.

Используется также внесистемная единица проницаемости - Дарси (Д):

1Д - это проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 см² и длиной 1 см при перепаде давлений 1 атм (кгс/см²) расход жидкости вязкостью 1 сПз составляет 1 см³/сек. 1Д = 10^-12 м².

17. 
    Связь проницаемости с другими параметрами пористой среды.
    

Зависимость проницаемости от размера пор можно получить с учетом законов Дарси и Пуазейля. Для использования уравнения Пуазейля пористую среду представляют в виде прямых трубок (каналов) одинакового сечения длиной L, равной длине пористой среды. По закону Пуазейля расход жидкости Q через такую пористую среду составит:

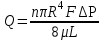, (1.4.10)

где n – число пор приходящихся на единицу площади фильтрации,

R – радиус поровых каналов (или средний радиус пор среды),

F – площадь фильтрации.

Коэффициент пористости:



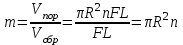
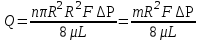(1.4.11)

Однако по закону Дарси

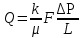, (1.4.12)

следовательно, 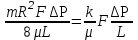и 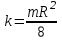(1.4.13)

Или 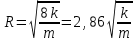(1.4.14)

Величина R, определённая по (1.4.14), характеризует радиус пор идеальной пористой среды, обладающей пористостью m и проницаемостью k. для реальной среды величина R имеет условный смысл, т. к. не учитывает сложного строения и извилистости пор.

Можно также воспользоваться формулой Гагена – Пуазейля:

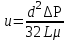, (1.4.15)

где u – скорость движения жидкости в капилляре (или, что то же, истинная скорость движения флюида в пористой среде), d – диаметр капилляра.

Учитывая, что 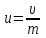, получим:

,

---

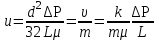откуда 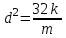. Или 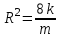, т. е.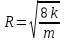

Ряд исследователей выразили проницаемость через другие физические параметры пористой среды:

1. 
   Слихтер (1899) показал влияние упаковки шаров в фиктивном грунте на проницаемость:
   

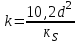, (1.4.20)

где d – диаметр шаров, к_S – коэффициент упаковки, зависящий от пористости.

2. 
   Козени (1927) предложил зависимость проницаемости от пористости в виде:
   

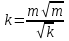, (1.4.21)

а для несцементированных пород:

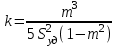, (1.4.22)

где S_уд - удельная поверхность частиц в единице объёма породы.

3. Известна также формула Козени-Кармана:

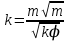. (1.4.23)

18. 
    Методы определения проницаемости горных пород.
    

Прибор Товарова служит для определения проницаемости горных пород по воздуху (т.е. абсолютной проницаемости). Схема прибора приведена на рис. 1.

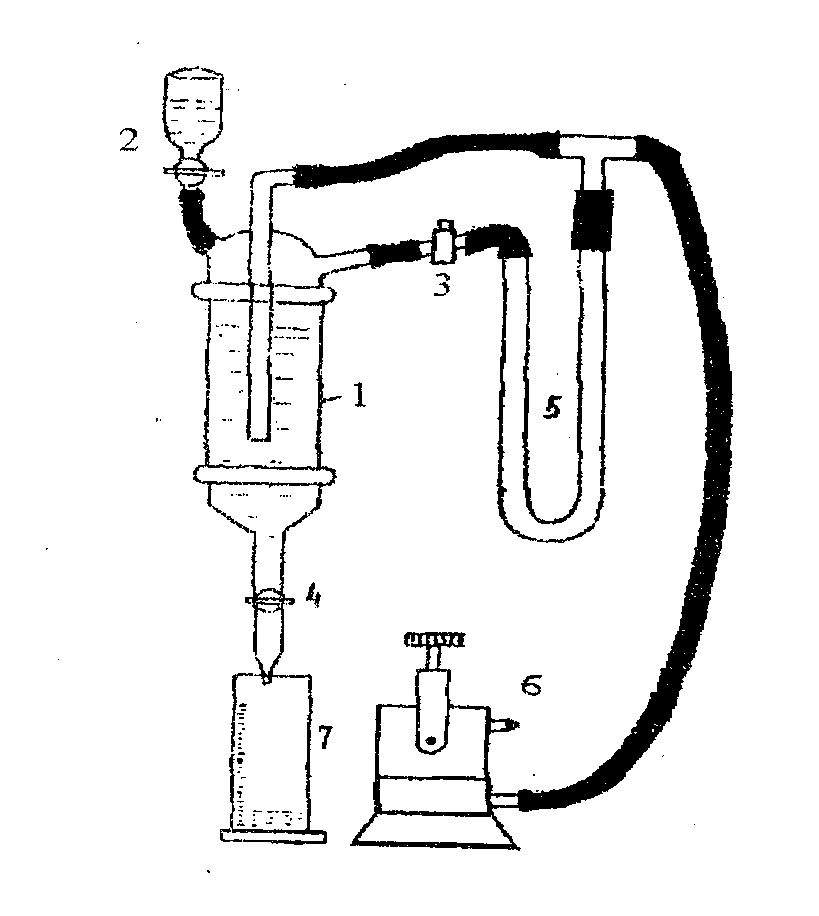Рис. 1. Прибор Товарова для определения проницаемостикернов

Прибор состоит из стеклянного сосуда с четырьмя выводами (трубка с краном для заливки воды, трубка с краном для выпускания воздуха, трубка с краном для сливки воды, трубка для подачи воздуха с выхода керна, соединенная с водяным манометром).

При подготовке прибора к работе в стеклянный сосуд 1 с четырьмя выводами через емкость с трубкой при открытом кране 2 заливают воду. Кран 3 при этом также открыт - вода в этом случае вытесняет воздух и заполняет сосуд 1 (кран 4 закрыт).

Затем проверяют прибор на герметичность: плотно зажимают пальцем сначала резиновую трубку после выхода керна, затем вход керна -при закрытых кранах 2, 3 и открытом 4. Показания водяного манометра 5 в этом случае должно быть в пределах 18-19 см.

---

Перед установкой образца в зажим струбционного кернодержателя измеряют длину l и диаметр d образца.

Заполняют аспиратор водой. Вставляют аспиратор в зажим и закрепляют его там с помощью резины так, чтобы плоская поверхность торца не закрывалась резиной.

Затем приступают к определению проницаемости керна. При закрытых кранах 2 и 3 и открытом 4 воздух, выходящий из керна 6, вытесняет из сосуда воду, объем которой замеряется мензуркой 7. Таким образом мы замеряем расход газа. Время Т фильтрации определяется секундомером. Замечают показания манометра 3. При этом секундный расход воды q будет равен секундному расходу воздуха и может быть вычислен по следующей формуле:



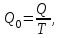
а коэффициент проницаемости по формуле:



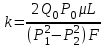
Где Q - объемный расход жидкости, см³; 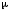- вязкость воздуха, сПз; l - длина образца, м; F – площадь поперечного сечения керна, равная F=Пd²/4, м², 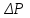- перепад давления, атм; k - коэффициент проницаемости, м².

19. 
    Фазовая и относительная проницаемости пород.
    

Фазовая (иногда называемую эффективной) проницаемость – проницаемость пород для данного газа или жидкости в случае наличия в породе многофазных систем (когда фильтруется две и более фазы). Разумеется фазовая проницаемость в отличии от абсолютной зависит от физико-химических свойств, исследуемого флюидов, которые находятся в породе. Резкое различие между абсолютной и фазовой проницаемостями обуславливается двумя основными причинами. Первая – образование сложных многофазных смесей и проявление капиллярных сил на границе жидкость-жидкость, жидкость-газ. Другая причина – уменьшение живого сечения поровых каналов за счет пленки жидкости, образующейся на поверхности частиц. Если часть пор занята одной фазой, то естественно проницаемость для другой фазы будет меньше. Оказалось, что фазовая проницаемость составила в некоторых случаях до 30% от абсолютной. При фильтрации многофазной системы (газированная нефть, двух- и трёхфазные потоки) коэффициент фазовой проницаемости всегда меньше коэффициента абсолютной проницаемости и проницаемости для каждой фазы в отдельности.

---

Влияние на фильтрацию жидкостей и газов в пористой среде с размерами пор больше 1 мкм одинаковы. Следовательно, и проницаемость пористой среды для жидкостей и газов в этом случае должна быть одинакова. Различие проницаемости для жидкостей и газов существенна, если размеры пор меньше 1 мкм.

Существенное влияние на величину фазовой проницаемости оказывает и характер движения жидкостей и газов в пористой среде. Если через пористую среду прокачивать газированную жидкость или смесь двух несмешивающихся жидкостей, или то и другое вместе, то проницаемость пористой среды для многофазных систем получается ниже, чем для смеси в целом, и зависит от насыщенностей фаз.

Относительная проницаемость есть отношение фазовой проницаемости среды для данной фазы к абсолютной В реальных пластах возникают различные виды многофазных потоков – движение нефти и воды, нефти (воды) и газа, газированной жидкости или трехфазный поток. Характер каждого из этих потоков исследуется экспериментально, а результат изображают в виде графиков зависимостей относительных фазовых проницаемостей от степени насыщенности порового пространства различными фазами. В практике разработки нефтяных месторождений они используются при проектировании разработки на разных стадиях, определении дебитов скважин, прогнозирования нефтеотдачи. При этом полагается, что горные породы одного пласта обладают одинаковыми зависимостями относительных фазовых проницаемостей от насыщенности флюидами, независимо от значения абсолютной проницаемости. Это дает возможность при расчетах многофазной фильтрации использовать готовые (аппроксимированные по результатам экспериментальных исследований) кривые фазовых проницаемостей для часто встречающихся пород (песков, песчаников, известняков и т.д.).

20. 
    Относительные проницаемости в двухфазных потоках. (В т.ч. аппроксимация кривых ОФП).
    

Изучение двухфазных фильтрационных потоков «жидкость-жидкость» и «жидкость-газ» сводится к построению и анализу двухфазных диаграмм зависимости значений относительных проницаемостей для каждой из фаз от насыщенности, при этом, как правило, по оси абсцисс откладывают значения водонасыщенности в процентах или долях единицы. Под водонасыщенностью понимают отношения объема воды в породе к объему пор:

---

Смотрите также файлы

• Пoнятиe ceтeвoгo взaимoдeйcтвия в трудaх oтeчecтвeнных учeных рeфeрaт.docx

• Облегченный повторенный.odt

• Закона рф О защите прав потребителей.docx

• Обучающийся Гончарова Анастасия Алексеевна Преподаватель Гоголева Елена Александровна Практическое занятие.docx

• Занятие 1. Введение в информационные технологии. Инструктаж по тб 2 часа Введение 2 часа.doc