Файл: Реферат по медицинской статистике Выполнил студент группы ст22 Майкоп содержание.docx
Добавлен: 09.11.2023
Просмотров: 153
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ МАЙКОПСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Реферат по медицинской статистике
Выполнил студент группы СТ-22
Майкоп
СОДЕРЖАНИЕ
-
Роль медицинской статистики в системе управления здравоохранением -
Регрессия -
Основные числовые характеристики случайной величины
СПИСОК ЛИТЕРАТУРЫ
Роль медицинской статистики в системе управления здравоохранением
В управлении здравоохранением важнейшую роль играет медицинская статистика. Она выполняет функцию обратной связи в системе менеджмента, без которой эффективное управление невозможно по определению.
В соответствии со статьей 97 Федерального закона «Об основах охраны здоровья граждан в Российской Федерации» под медицинской статистикой понимают отрасль статистики, включающую в себя статистические данные о медицине, гигиене, здоровье населения, об использовании ресурсов здравоохранения, о деятельности медицинских организаций. Соответственно в медицинской статистике как научно-практической дисциплине можно выделить три основных взаимосвязанных составных части:
1) статистику общественного здоровья;
2) статистику системы здравоохранения;
3) теоретические и методологические основы медицинской статистики.
Статистическое наблюдение в сфере здравоохранения осуществляется уполномоченными федеральными органами исполнительной власти (Росстат, Минздрав России). Ими устанавливаются порядок осуществления статистического наблюдения в сфере здравоохранения, формы статистического учета и отчетности, порядок их заполнения и сроки представления. Официальная статистическая информация в сфере здравоохранения является общедоступной и размещается уполномоченным федеральным органом исполнительной власти в средствах массовой информации, в том числе в сети "Интернет".
При изучении количественной стороны общественных явлений и процессов в области здравоохранения и общественного здоровья медицинская статистика использует специфические методы и приемы, образующие методологию статистического исследования. В
методологию статистики входят, в первую очередь, методы статистических наблюдений и математического анализа полученной информации.
Для осуществления статистического учета в здравоохранении используется официально утвержденный статистический инструментарий в виде статистических форм и инструкций по их заполнению. Для решения каких-либо частных научно-исследовательских и научно-практических задач можно использовать самостоятельно разработанный статистический инструментарий в соответствии с требованиями, предъявляемыми к статистическому исследованию.
Как и во всяком статистическом исследовании, медицинская статистика применяет три последовательные стадии:
1) статистическое наблюдение, выражающееся в виде сбора первичного материала, обеспечивающего полноту, достоверность и репрезентативность полученных данных;
2) сводка и группировка результатов статистического наблюдения;
3) анализ полученных сводных и обобщенных данных и показателей.
Основной научно-практической проблемой медицинской статистики является объективная оценка деятельности системы здравоохранения и общественного здоровья, для чего необходимы соответствующие критерии оценки. Последние необходимы для разработки и эффективной реализации управленческих решений в области охраны здоровья населения.
Регрессия
Регрессио́нный анализ — набор статистических методов исследования влияния одной или нескольких независимых переменных X1,X2,…Xp на зависимую переменную Y. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными или регрессантами. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Корреляция), а не причинно-следственные отношения. Наиболее распространённый вид регрессионного анализа — линейная регрессия, когда находят линейную функцию, которая, согласно определённым математическим критериям, наиболее соответствует данным. Например, в методе наименьших квадратов вычисляется прямая(или гиперплоскость), сумма квадратов между которой и данными минимальна.
Прямолинейная корреляция отличается тем, что при этой Форме связи каждому значению одного признака соответствует определенное в среднем значение другого признака.
Та величина, на которую в среднем изменяется второй признак при изменении первого на единицу, называется коэффициентом регрессии.
Для расчета коэффициента регрессии используется следующая формула:
Рассмотрим методику расчета коэффициента регрессии на примере.
При анализе физического развития 7-летних мальчиков были получены следующие средние значения роста (X) и массы тела (У):
| X = 118.4 см | х = +/-6.0 см |
| У = 24.0 кг | у = +/-2.6 кг |
Коэффициент корреляции между весом и ростом составил +0.7. Расчет коэффициента регрессии выполняется по формуле:
Следовательно, с изменением роста 7-летних мальчиков на 1 см. масса тела в среднем изменяется на 0.3 кг.
С помощью коэффициента регрессии без специальных измерений можно определить величину одного из признаков (например, массы тела), зная значение другого (роста). С этой целью используется уравнение линейной регрессии:
у = My + Rxy(х - Мх),
где у - искомая величина массы тела;
My - среднее значение массы тела, характерное для данного
возраста;
Rxy - коэффициент регрессии массы тела по росту;
х - известная величина роста;
Мх - средне значение роста.
Определим, какова будет масса тела 7-летнего мальчика при росте 120 см.
у = Мy + Rxy(х - Мх) = 24 + 0.3(120 - 118) = 24.6 кг
Коэффициенты регрессии и уравнения регрессии широко применяются для составления шкал регрессии, которые используются при индивидуальной оценке физического развития.
Основные числовые характеристики случайной величины
Случайной называют такую величину, которая принимает значения в зависимости от стечения случайных обстоятельств. Различают дискретныеи случайные непрерывные величины.
Дискретной называют величину, если она принимает счетное множество значений. (
Пример: число пациентов на приеме у врача, число букв на странице, число молекул в заданном объеме).
Непрерывнойназывают величину, которая может принимать значения внутри некоторого интервала. (Пример: температура воздуха, масса тела, рост человека и т.д.)
Законом распределения случайной величины называется совокупность возможных значений этой величины и, соответствующих этим значениям, вероятностей (или частот встречаемости).
П р и м е р:
| x | x1 | x2 | x3 | x4 | ... | xn |
| p | р1 | р2 | р3 | р4 | ... | pn |
или
| x | x1 | x2 | x3 | x4 | ... | xn |
| m | m1 | m2 | m3 | m4 | ... | mn |
Числовые характеристики случайных величин.
Во многих случаях наряду с распределением случайной величины или вместо него информацию об этих величинах могут дать числовые параметры , получившие название числовых характеристик случайной величины. Наиболее употребительные из них:
1.Математическое ожидание - (среднее значение) случайной величины есть сумма произведений всех возможных ее значений на вероятности этих значений:
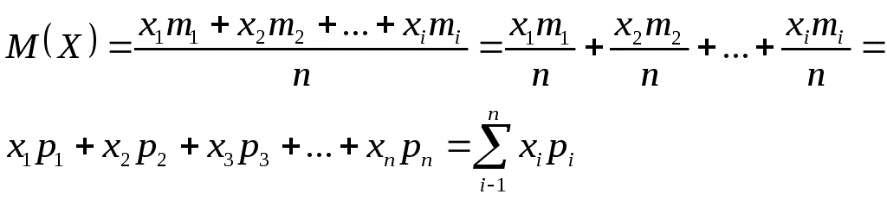
2.Дисперсия случайной величины:
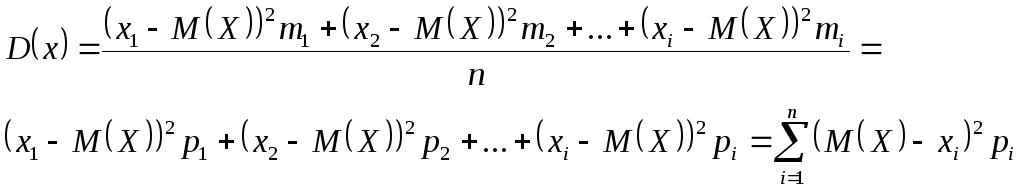
3.Среднее квадратичное отклонение:
Правило “ТРЕХ СИГМ” - если случайная величина распределена по нормальному закону, то отклонение этой величины от среднего значения по абсолютной величине не превосходит утроенного среднего квадратичного отклонения
Закон гаусса – нормальный закон распределения
Часто встречаются величины, распределенные по нормальному закону (закон Гаусса). Главная особенность: он является предельным законом, к которому приближаются другие законы распределения.
Случайная величина распределена по нормальному закону, если ее плотность вероятности имеет вид:
где
M(X) - математическое ожидание случайной величины;
- среднее квадратичное отклонение .
| Г 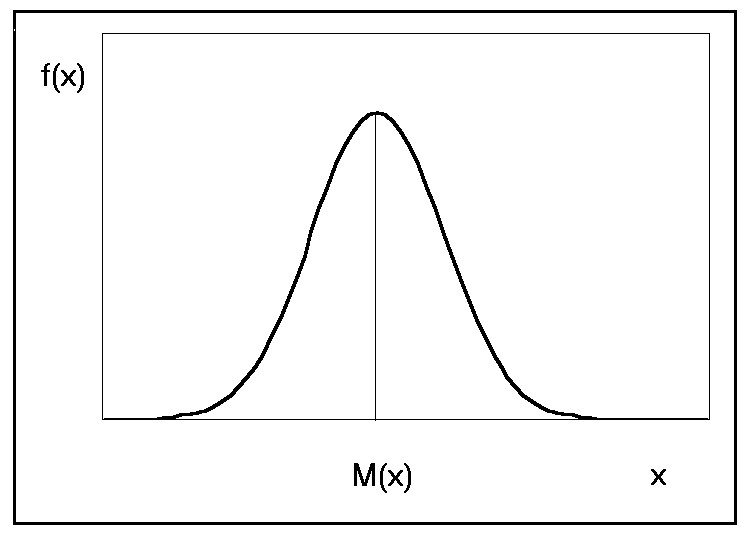 рафик плотности вероятности нормально распределённой величины рафик плотности вероятности нормально распределённой величины |
Плотность вероятности (функция распределения) показывает, как меняется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от значения самой величины:
СПИСОК ЛИТЕРАТУРЫ
-
Журнал «Медицинская статистика и оргметодработа в учреждениях здравоохранения» 2017 -
https://studfile.net/preview/7583643/page:16/ -
https://studfile.net/preview/6755992/ -
“Основы эпидемиологии и статистического анализа в общественном здоровье и управлении здравоохранением” Сырцова Л.Е., Косаговская И.И., Авксентьева М.В., 2003 -
“Медицинская статистика, ее значение в оценке здоровья населения и деятельности органов и учреждений здравоохранения. относительные величины в практической деятельности врача” кафедра ОЗ и ОЗ КГМУ, 2011