Файл: Цехта 6 мотор бар. рбір мотор шін оны азіргі уаытта осулы болу ытималдыы 0,8 райды. азіргі уаытта 4 озалтыш осыландыыны ытималдыын табыыз.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 09.11.2023

Просмотров: 92

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


1 билет

1.Нақты сандар. Жиындардың қуаты

2.Нанотехнология және наноматериалдар

3.математика есеп

а) Цехта 6 мотор бар. Әрбір мотор үшін оның қазіргі уақытта қосулы болу ықтималдығы 0,8 құрайды. Қазіргі уақытта 4 қозғалтқыш қосылғандығының ықтималдығын табыңыз.
Б)физика есеп

Нақты сандар.

Нақты сандар жиыны

1. Натурал сандар


Натурал сандар деп мына сандарды атаймыз 0, 1, 2, 3, 4,…

Барлық натурал сандар жиының N символымен белгіленеді. Белгілі бір a санының натурал сан екенің көрсету үшін a ∈ N деп белгілейміз. Мысалы 1 ∈ N, 5 ∈ N, 3 ∈ N.

2. Бүтін сандар


Бүтін сандар деп оң және теріс таңбасымен алынған барлық натурал сандар жиынынан құралған сандар жиының атаймыз.

Яғни бүтін сандар 0, 1, 2, 3, 4,… және –1, –2, –3, –4,… сандар жиындарының бірігуінен құралған. Бүтін сандар жиының P символымен белгілейміз.

Тұжырым.

N жиынына еңетің кез келген сан P жиынына да еңеді. Бұндай жағдайда N жиыны P жиынына еңеді дейді, және N ⊆ P деп жазады.

3. Рационал сандар

Рационал сандар деп 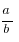  (a ∈ P, b ∈ P, b ≠ 0) сандарын атаймыз. Мысалы  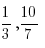. Рационал сандар жиының R деп белгілейміз.
Кез келген бүтін c саны рационал жиынына еңеді да, яғни рационал саны да болып табылады. Өйткені 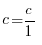 , соңдықтан P ⊆ R.

4. Иррационал сандар


Иррационал сан деп π = 3,141592… немесе 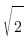  = 1,4… сандары тәрізді бөлшек бөлігі шексіз, периодты емес цифрлардан құралған сандарды атаймыз.

Иррационал сандар жиының Q деп белгілейміз.

5. Нақты сандар


Нақты сандар жиыны деп барлық– натурал, бүтін, рационал және иррационал сандардан құралған сандар жиының атаймыз. Және бұл жиынды Z әрпімен белгілейміз.

Нақты сандар Олар натурал сандарды, бүтін сандарды, рационалды және иррационалдарды қамтитын сандық жиынты құрайды. Олар ℝ немесе жай белгісімен белгіленеді R және олардың ғылымда, техникада және экономикадағы ауқымы соншалықты, «сан» туралы айтқанда, бұл нақты сан екені түсінікті.

Нағыз сандар ежелден бері қолданылып келеді, дегенмен оларға бұл атау берілмеген. Пифагор өзінің атақты теоремасын жасаған кезден бастап натурал сандардың немесе бүтін сандардың квотасы ретінде алуға болмайтын сандар пайда болды.

«Нақты сан» терминін көп математикалық теңдеуді шешуден туындайтын түбірлердің екі түрін ажырату үшін ұлы математик Рене Декарт (1596-1650) жасаған.

Бұл түбірлердің кейбірі теріс сандардың жұп түбірлері болуы мүмкін, Декарт бұл «ойдан шығарылған сандар» деп атады, ал болмағандары нақты сандар болды.

Номинал уақыт өте келе сақталып, екі үлкен сандық жиынтығын тудырды: нақты сандар мен күрделі сандар, нақты сандар, қиял сандар және нақты және жартылай қиялдан тұратын үлкен жиын.

Нақты сандардың эволюциясы өз бағытын 1872 жылға дейін жалғастырды, математик Ричард Дедекинд (1831-1936) деп аталатындар арқылы нақты сандар жиынтығын ресми түрде анықтады. кесу Dedekind. Оның жұмысының синтезі сол жылы жарық көрген мақалада жарияланды.

Нақты сандардың қасиеттері


-Нақты сандарға натурал сандар, бүтін сандар, рационал сандар және иррационал сандар жатады.

-Қосудың ауыстырымдылық қасиеті орындалады: қосындылардың реті соманы өзгертпейді. Егер a және b екі нақты сан болса, бұл әрқашан дұрыс:

a + b = b + a

-0 қосындысының нейтралды элементі: a + 0 = a

-Жалпы сомаға ассоциативті меншік орындалады. Егер a, b және c нақты сандар болса: (a + b) + c = a + (b + c).

-Нақты санның қарама -қарсы мәні --a.

-Айыру керісінше қосынды ретінде анықталады: a -b = a + (-b).

-өнімнің коммутативті қасиеті орындалды: факторлардың реті өнімді өзгертпейді: a.b = b.a

-Өнімде ассоциативті қасиет те қолданылады: (a.b) .c = a. (B.c)

-1 көбейтудің бейтарап элементі: a.1 = a

-Көбейтудің қосуға қатысты үлестіргіш қасиеті дұрыс: а. (b + c) = a.b + a.c

-0-ге бөлу анықталмаған.

-А -ның кез келген нақты саны, 0 -ден басқа, кері көбейткішке ие-1 осылайша А.-1 = 1.

-Егер а нақты сан болса: а0 = 1 және a1 = а.

-Нақты санның абсолюттік мәні немесе модулі -бұл сан мен 0 арасындағы қашықтық.

Нақты сандармен орындалатын амалдар


Нақты сандармен басқа сандық жиындармен орындалатын амалдарды орындауға болады, соның ішінде қосу, алу, көбейту, бөлу, күшейту, радиация, логарифмдер және т.б.

Әдеттегідей, 0 -ге бөлу анықталмаған, сандардың теріс логарифмдері де, 0 де жоқ, дегенмен лог 1 = 0 және 0 мен 1 арасындағы сандар логарифмдері теріс екені рас.

Жиындардың қуаты

Берілген А және В ақырлы жиындарының қуаттарының теңдігін олардың элементтерін санау арқылы білуге болады. Мысалы, A={a, b, c, d, e, f}; B={α, β, γ, δ, ε, ζ}; |A| = |B| =6.

Жиындардың теңдігін білудің басқа да жолы бар:


A

a

b

c

d

e

f


B

α

β

γ

δ

ε

ζ


Егер а A үшін бір ғана bB сәйкес болса және керісінше әрбір bB үшін бір ғана aA сәйкес болса, онда А және В жиындарының арасында өзара бір мәнді сәйкестік бар дейді.Мұндай жиындар эквивалентті немесе тең қуатты жиындар деп аталады. Айталық N натурал сандар жиыны болсын 1, 2, 3, 4, 5, …, M – олардың квадраттарының жиыны: 1, 4, 9, 16, 25, …Олай болса, N M. Натурал сандар жиынына эквивалентті жиындар саналымды жиындар деп аталынады. Саналымды жиын туралы мынадай теорема бар:


1-Теорема. Қандай да бір жиын саналымды болу үшін, оның элементтерін шексіз тізбек түрінде кескіндеу қажетті және жеткілікті.

2-Теорема. Саналымды жиынның кез-келген ішкі жиыны саналымды жиын.

3-Теорема. Ақырлы немесе саналымды жиындардың бірігуі-саналымды жиын.

Салдар. Рационал сандар жиыны саналымды жиын. Шынында да барлық оң рационал сандарды шексіз кесте түрінде өрнектеуге болады:

1/1, 1/2, 1/3, 1/4, 1/5, …

2/1, 2/2, 2/3, 2/4, 2/5, …

3/1, 3/2, 3/3, 3/4., 3/5, …

4/1, 4/2, 4/3, 4/4, 4/5, …

…………………………,

Бұл кестені сол жақ жоғарғы бұрыштан бастап диагональ бойымен айналуға болады. Бірақ барлық шексіз жиындар саналымды емес.

Кантор теоремасы. [0;1] кесіндісіндегі барлық нақты сандар жиыны саналымды емес. Теореманы кері жорып дәлелдейміз . Айталық бұл жиын саналымды болсын. Демек, бұл жиынның барлық элементтерін шексіз тізбек түрінде өрнектеуге болады.

Α1 = 0,а11а12а13а14…

Α2 = 0,а21а22а23а24…

Α3 = 0,а31а32а33а34…

………………………

Төмендегі тәртіппен В = b1b2b3b4… шексіз ондық бөлшек тізбегін b1 ≠ a11, b2 ≠ a22, b3 ≠ a33 және т.б. құрайық. Бұл бөлшек айтылған тізбекке енбейді, себебі тізбектің бірінші мүшесінен оның бірінші цифры өзгеше, екіншісінен екінші цифры өзгеше т.б. Ендеше [ 0;1] кесіндісінің барлық нақты сандар жиыны саналымды емес. Бұл жиынның қуаты континуум (С қуатты), ал С қуатты жиын континуальды жиын деп аталады.

Теорема. [a,b] кесіндісінің бардлық нақты сандар жиыны континуум қуатты.

Шынында да y=a+(b - a)x функциясы [ 0; 1] және [ a; b] кесіндісінің нүктелерінің арасында өзара бір мәнді сәйкестік орнатады, демек [ a; b] кесіндісіндегі нақты сандар жиынының қуаты [ 0; 1] кесіндісіндегі нақты сандар жиынының қуатындай.

Теорема. Континуум қуатты ақырлы немесе саналымды жиындардың жиыны – континуум қуатты жиын болып табылады.

1 Салдар. Барлық нақты сандар жиыны континуум қуатты.



2 Салдар. Барлық иррационал сандар жиынының қуаты С. I =R / Q

2.Нанотехнология және наноматериалдар

«НАНОТЕХНОЛОГИЯ ЖӘНЕ НАНОМАТЕРИАЛДАР» БӨЛІМІНІҢ ФИЗИКА ПӘНІНДЕГІ РӨЛІ
Нанотехнология (грек. nanos – ергежейлі және технология) - бұл көзге көрінбейтін аса ұсақ бөлшектерді ретке келтіре отырып, соның ерекшеліктерін алдын ала белгілеп беру арқылы әлдебір құрылымды құрастыруға қажетті жекелеген атомдарды ыңғайластыра орналастыру. Нанотехнология – кеңістіктің нанометрлік аймағындағы жеке атомдарға, молекулаларға, молекулалық жүйелерге әсер ету арқылы жаңа физика-химиялық қасиеттері бар молекулалар, наноқұрылымдар, наноқұрылғылар мен материалдар алу мүмкіндіктерін зерттейтін қолданбалы ғылым. Нанометр дегеніміз бір метрдің миллиардтан бір бөлігі. Нанотехнология осындай ауқымды өлшемдермен айналысады.[2]


Нанотехнология термині 1947 жылы Норио Танигучи тарапынан енгізілді және оған «өте жоғары дәлдік және ультракіші өлшемді 1 нм алуға мүмкіндік беретін өндіріс технологиясы» анықтамасы берілді. 1980-1990 жылдары Эрик Дрекслер кітабында нанотехнология жеке молекулалардан құрылғы жасап шығау деп түсіндірілді. Нанометрдің келешегі ретінде төмендегілер жазылды. Мысалы, кішкентай автономды нанороботтар адам ағзасына енгізіліп, қан жүйесі бойынша жүзіп ауыру органдарды табады және оларды «жөндеуді» іске асырады. Нанотехнология ғылымның облысы терінде түсіндірілді. Бірақ Альберт Франкстың 1987 жылғы нанотехнологияға берген анықтамасы айтарлықтай шындыққа жанасады: «Нанотехнология – бұл 0,1-100 нм аралығындағы өлшемді және дәлділіктегі өндірістер».

Нанотехнология сөзі салыстырмалы жаңа болғанымен, нанометрлік өлшемдегі қондырғылар мен құрылымдар жаңа түсінік емес. Іс жүзінде олар Жер бетінде тіршіліктің пайда болуымен бірге қалыптасқан. Моллюск мұхит сақ құлағы мықты бор наноталшықтарының ақуыздың көміртегімен қоспасын жабыстыра отырып, өте берік ішінен құйылатын бақаншақты өсіреді. Сыртында пайда болған жарықтар, бақаншақтарда наноқұрылымдалған кірпіштердің болуынан тарала алмайды. Бақаншақтар табиғи көрсету болып табылады, өйткені нанобөлшектерден құралған құрылымдар, біртекті көлемде материалдардан біршама мықтырақ болады. Қай уақыттан бастап адамдардың бірінші рет наноөлшемді материалдарды пайдалана бастағаны анық емес. Б.з. IV ғасырында римдік шыны қайнатушылар құрамында металдың нанобөлшектері бар шыны жасады. Бұл дәуірдің Британ мұражайында орналасқан Ликура деп аталатын бұйымдары бар. Кесе Ликураның өлімін бейнелейді, ол натрий әгінің негізіндегі құрамында күміс және алтын нанобөлшегі бар шыныдан жасалған. Оған жарық көзін орналастырғанда кесенің түсі көктен күңгірт-қызыл түске ауысады. Орта ғасыр мұрағаттың (храм) түсінің құбылуы шыны құрамындағы металдық нанобөлшектердің қатысуымен түсіндіріледі.

Өте кішкентай бөлшектердің потенциалдық маңыздылығы туралы ирландық химик Роберт Бойль 1661 жылы «Химик-скептик» жұмысында талқылады. Мұнда Бойль Аристотельдің төрт негізден (жер, су, от және ауа) тұратын материяға көзқарасын сынға алады. Олардың бойына Бойль заттың кішкентай бөлшектері әр түрі тәсілмен байланысады деп түсінді және оларды корпускулалық деп атаған. Бойль оларды түзуші бөлшектері кішкентай массалар немесе кластерлерге қиын ыдырайды деп болжады. XVIII-XIX ғасырлардағы фотосурет жетілген және алдыңғы қатардағы технология күміс нанобөлшектерінің жарық әсерінен пайда болуына негізделген. Фотопленка – мөлдір ацетат цеюлоза негізіне жағылған күміс галогенидінің эмульсиясы (мысалы, желатиндегі күміс бромиді). Жарық күміс галогениді күмісті таза нанобөлшектеріне ыдыратады, олар өрнектің пикселдері болып табылады. Эектромагниттік өрістің теориясын ойлап тапқан Джеймс Клерк Максвелл 1861 жылы бірінші рет түсті фотосуретті алды. 1883 жылдың шамасында «Кодак» корпорациясының негізін қалаған америкалық өнер тапқыш Джордж Истмэн күміс галогенидімен қапталған ұзын қағаз жолақтарынан тұратын пленканы жасады.


XIX ғасырда нанотехноогиялық көзқарастың қызықты мысалдарын Д.Максвеллдің «демонында» қарастыруға болады. Молекулаларды жылдамдығы бойынша жіктеу және солақай Лесковтың ескі «жоғары-төмен» әдісімен «наношегелерді» дайындап, оны «ағылшын» бүргемен (микроқұрылыстың өзіндік аналогы) тұжырымдады. Н.С. Лесков осы шегелердің басындағы жазуларды тек микроскопта 5 000 000 есеге дейін үлкейтіп көруге болатынын 1881 жылы белгіледі.[1]

Аңыз-ертегілердегі аспанға ұшатын ағаш ат пен кілем, желаяқ етіктер, аста-төк дастарқан, қияндағыны көз алдыңа алып келетін қол айна секілділер шындыққа айналып, дәл қазір "көне дүниелер" санала бастады. Нанотехнология да өмірге осындай қиял мен әуестік нәтижесінде келген еді. 1986 жылы студент Эрик Дрекслер өзінің "Жасампаз машина" аталатын футуристік эссесінде тұңгыш рет молекулярлы технология атауын қолданады. Ол фантаст-жазушы Станислав Лемнің идеяларына өз қиял-болжамдарын қосақтай отырып, "Саналы тіршілік ортасының" жалпы бет-бейнесін жасап шығады. Осы болжамға сәйкес, XXI ғасырда нанороботтар әрбір заттың, әрбір адам ағзасының ішіне енгізіледі де, адамзат қоршаған әлеммен бірге тұтастай саналы компьютерге айналады. Мұндай идея Эссе Дрекслерден бұрынырақ пайда болған көрінеді. 1981 жылы ІВМ корпорациясының швейцариялық филиалындағы екі инженер, Герд Бинниг пен Гейнрих Рорер мәнерлеп туннельдеуші микроскоп ойлап тауыпты. Микроскоптың құрылымы аса қарапайым: шамалы қысымға қосылған аса жіңішке ине бір нанометр шамасындағы қашықтықта материалдың үстімен жылжып отырады. Осы кезде инелердің өткір ұшы материалдың беткі қабатына электрондарды тесіп өткізеді де, соның нәтижесінде шамалы тоқ пайда болады, оның көлемі ине мен беткі қабаттың арасындағы қашықтыққа байланысты болады. Осылайша материалдың беткі қабатынан жекелеген атомдарды "ажыратуға" мүмкіндік туады. Бұл ғылымның пайда болуын 1959 жылы Нобель сыйлығының лауреаты, АҚШ физигі Р.Фейнманның жеке атомдарды манипулятор көмегімен қозғалту мүмкіндіктері туралы жасаған баяндамасымен байланыстырады. Нанотехнология терминін қолданысқа алғаш рет 1974 жылы жапон физигі Норио Танигути енгізген. Макроскопиялық заңдылықтарға сүйенетін басқа инженер ғылымдардан нанотехнологияның негізгі ерекшелігі, нанонысандар үшін кванттық және молекулааралық өзара әсерлесуінің күшті болуына байланысты. Нанотехнология саласындағы зерттеулер қазірдің өзінде практикалық маңызы зор нәтижелер беруде.

Нанотехнология әлемдік ғылым мен техникада соңғы 15-20 жылдарда пайда болған пәнаралық бағыт болып есептеледі, өлшемі 0,1-100 нм болатын объектіні қарастырады. Осы ғылыми техникалық бағыттың ең маңызды құраушысы – наноқұрылымдық материалдарды құру. Наноқұрылымдық (нанокомпоненттер, нанофазалы, наноталшықты және т.б) материалдар деп негізгі құрылымдық элементтері (кристалиттер, талшықтар, қабаттар, қуыстар) 100 нм-ден аспайтын материалдарды айтады. Материалтанулық зетрреу міндеттеріне қолайлы наноқұрылымдардың бөінетін құрылымды материалдары мен қасиеттері арасындағы мықты байланыспен іске асырылады. Наноқұрылымдық материалдар (наноматериалдар) өздерінің ерекше қасиеттерінің арқасында бүгінгі материалтану саласында жетекші орын алады.


Сканерлеуші электронды микроскоп (scanning electron microscope – SEM) – трансмиссиялы электрондық микроскопқа қарағанда басқаша , жәнеде басқа әдістермен жұмыс жасайды. Сканерлеуші электронды микроскопта диаметрі 1мкм шамасындағы электронды сәуле, зерттелетін заттың барлық бетін мұқият сканерлейді. Беттің тофограпиясының кішігірім өзгерістері , қуат ағынына жойқын әсер етеді. SEM – нің басқаша атауы – растрлық электрондық микроскоп.

Көру мүмкіндігі – атомдық, механикалық жергілікті, пьезоэлектрлікті, адгезионды және трибологиялық сипатамасын, магнитті материалдарды, доменді құрылымын, жартылай өткізгіштерді, төсеніштің морфологиясын, қоспаның таралуын, гетерошекаралар мен p-n ауысу шекарасын, фазаралық шекараны, жұқа органикалық пленкалардың беткі қабаттың морфологиясын анықтайды. Бұл микроскоптар көмегімен үлгінің үш өлшемді беткі кескінін бір нанометрге дейін алуға болады. Сенсор ретінде вольфрамды зонд қолданылады, туннелді, атомды-күшті модел ретінде өлшеулер жүргізіледі және электрохимиялық ерітіндімен өңдеу арқылы бастапқы қалпына келтіруге болады.

Микросхеманың қолданылатын элементтерінің сызықтық өлшемдерін кішірейту микроэлектрониканың ең негізгі мəселелерінің бірі болып табылады. Өлшемдері бірнеше немесе ондаған нанометр болып келетін схемалардың элементтерін құрастыру электрониканы сапалы түрде өзгертеді жəне оны наноэлектроника деп аталатын жаңа ғылыми сала зерттейді. Сонымен қатар элементтер жұмысының физикасы да өзгеретін болады.Олар негізінен кванттық механика принциптерінде жұмыс істейтін болады . Интегралды наноэлектронды кванттық схемаларды құрастыру нанотехнологияның түпкі мақсаты болып табылады. Нанотехнологияны зерттелетін үлгі бетінде наноөлшемдерге ие болатын, сонымен қатар жекелеген атомдар мен молекулалардан тұратын функционалды элементтерді құрастыру əдістері менамалдарының қосындысы ретінде анықтауға болады. Жартылай өткізгіш пластинаның бетіне маска жасауды қосатын жəне кейіннен микролитографияны, соның ішінде рентгендік, электрондық жəне иондық литографияны қолданатын дəстүрлі əдістерді қолдану болашақта наноөлшемді көлденең өлшемдері бар қатарларды қалыптастыруға мүмкіндік береді . Алайда жеке молекулалар мен атомдар негізіндегі элементтерді дəстүрлі жолдармен құрастыру мүмкін емес. 1980 жылы ІВМ фирмасының Швейцариядағы бөлімшесінің қызметкерлерімен бірге Г. Биннинг жəне Г. Рорермен құрастырған сканерлеуші туннельдік микроскоп өлшемдері 0,01 нм болатын металдық жəне жартылай өткізгіш төсеніштер зақымданбмай бақылауға жəне анализдеуге мүмкіндік берді .

Смотрите также файлы